OPTIMIZATION OF THE FORCE SENSOR CHARACTERISTICS BY THE FINIT ELEMENTS METHOD

Вергазов И.Р.¹, Тареева Ю.А.², Петрин В.А.³

¹ Соискатель,

²аспирант,

³соискатель,

Пензенский государственный университет

ОПТИМИЗАЦИЯ ХАРАКТЕРИСТИК ЧУВСТВИТЕЛЬНОГО ЭЛЕМЕНТА ДАТЧИКА СИЛЫ МЕТОДОМ КОНЕЧНЫХ ЭЛЕМЕНТОВ

Аннотация

Предложена конструкция чувствительного тензорезистивного элемента датчика силы. Методом конечных элементов определены зоны размещения тензорезисторов, обеспечивающие повышение чувствительности и линейности.

Ключевые слова: тензорезистивный датчик силы, зоны равной деформации, метод конечных элементов.

Vergazov I.R.¹, Tareeva Yu.A.², Petrin V.A.³

¹ applicant,

²post graduate student,

³applicant,

Penza State University

OPTIMIZATION OF THE FORCE SENSOR CHARACTERISTICS BY THE FINIT ELEMENTS METHOD

Abstract

The design of the strain gage force sensor is proposed. The zone of strain gage placing that provide sensitivity and linearity increasing are defined by finite elements method.

Keywords: strain gage force sensor, zone of equal strain, finite elements method.

Чувствительные элементы (ЧЭ) датчиков служат для измерения физических величин, таких как сила, давление, крутящий момент и др. Точность, чувствительность и стабильность метрологических характеристик средств измерений определяются в основном именно свойствами ЧЭ.

Дополнительно к ЧЭ предъявляются требования: стойкости к воздействию влияющих величин, высокой временной стабильности характеристик и релаксационной стойкости, малых влияний дестабилизирующих факторов, например, температуры окружающей среды, изменений атмосферного давления, при условии, что эти параметры не являются измеряемыми величинами [1 - 6].

Типичная конструкция датчика силы стержневого типа состоит из цилиндрического ЧЭ, на наружной поверхности которого установлены тензорезисторы и компенсационные сопротивления. Достоинство стержневых ЧЭ заключается в простоте изготовления. Для таких элементов достаточно легко достигаются высокие классы точности выполнения геометрических размеров, чистоты обработки поверхностей. Кроме того, стержневой упругий элемент наиболее подходит для построения датчиков на высокие пределы измерения при ограниченной массе и габаритных размерах.

Одним из недостатков такого ЧЭ является невысокая чувствительность. Для увеличения чувствительности стержень выполняют в виде полого цилиндра. Изменение конструкции ЧЭ требует решения задачи оптимизации расположения элементов тензометрической измерительной цепи на упругих элементах УЭ с целью увеличения чувствительности и линейности функции преобразования.

Выходной величиной УЭ датчиков механических величин является линейное или угловое перемещение или деформация. Под перемещением будем понимать прогибы характерных точек УЭ в направлении, задаваемом направлением действия нагрузки. Под деформацией будем понимать перемещение точек, лежащих на поверхности УЭ.

Если УЭ выполнен в форме цилиндрического стержня и к нему приложена продольная растягивающая сила Fp, то под действием этой силы стержень получит удлинение Δl, которое в соответствии с законом Гука будет равно

,

где S – сечение стержня; E– модуль упругости материала [7].

Вследствие неоптимального расположения тензоэлементов снижается точность измерения за счет непропорционального изменения сопротивлений плеч измерительной цепи, что в свою очередь приводит к повышению нелинейности.

Аналитический расчет деформаций для УЭ в виде стержня сложной геометрической формы является громоздким и может быть выполнен только приближенно можно Определить деформационные характеристики исследуемого УЭ с учетом конструктивных особенностей можно при помощи численного моделирования методом конечных элементов (МКЭ).

В рассматриваемом случае исследовались деформации УЭ в виде стержня с двумя отверстиями, одно из которых проходит через центр боковой грани УЭ и является сквозным, а второе расположено в основании УЭ и углубляется внутрь УЭ на конструктивно заданную глубину. На двух других плоских гранях УЭ расположены элементы измерительной цепи.

Для оптимизации расположения элементов тензометрической цепи на поверхности УЭ необходимо определить зоны максимальных равных по модулю и противоположных по знаку деформаций на плоской грани стержневого УЭ тензорезисторного датчика силы.

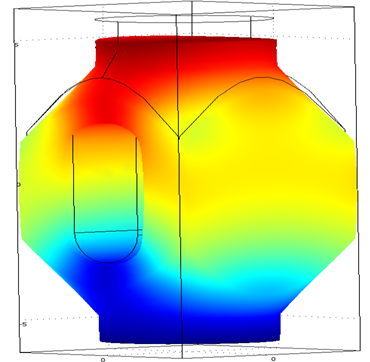
Для анализа полученных моделей использовалась программа моделирования с помощью МКЭ Comsol, позволяющие рассчитывать и анализировать физические процессы, протекающие при деформациях УЭ. Распределение механических напряжений по Мизесу на поверхности УЭ показано на рисунке 1.

Результатом моделирования стало получение набора точек на поверхности боковой плоской грани УЭ с соответствующими этим точкам относительными деформациями боковой грани УЭ.

Рис. 1 – Распределение механических напряжений по Мизесу на поверхности УЭ

При помощи математических пакетов типа Matlab были найдены аналитические зависимости, описывающие продольные и поперечные деформации. Для этого строились поверхности, описываемые полиномами по точкам, полученным при моделировании УЭ с помощью МКЭ. Поверхность, соответствующая поперечным деформациям боковой плоской грани УЭ, представлена на рисунке 2.

Рис. 2 – Поверхность, соответствующая поперечным деформациям боковой плоской грани УЭ

Линии с одинаковыми деформациями для размещения тензоэлементов на боковой грани УЭ показаны на рисунке 3.

Рис. 3 – Линии с одинаковыми деформациями для размещения тензоэлементов, воспринимающих продольные деформации.

Меняя конструктивные размеры УЭ, а также форму и местоположение отверстий, можно добиться увеличения чувствительности МЭМС датчика в целом и обеспечения линейности его выходного сигнала.

Литература

1. Мокров Е.А., Баринов И.Н., Цибизов П.Н. Полупроводниковые пьезочувствительные элементы микроэлектронных датчиков давлений. Основы проектирования и разработки: учеб. пособие - Пенза: Изд-во Пенз. гос. ун-та, 2009. - 104 с.
2. Баринов И.Н., Цыпин Б.В. Состояние разработок и тенденции развития высокотемпературных тензорезистивных датчиков давлений на основе карбида кремния // Приборы и системы. Управление, контроль, диагностика.−2010.− №11.−С. 50-60.
3. Волков В.С., Баринов И.Н. Использование системы Simulink при имитационном моделировании высокотемпературных полупроводниковых датчиков давления // Приборы.- 2011. - . № 7. - с. 50 – 55.
4. Волков В.С., Баринов И.Н. Полупроводниковые датчики давления на основе резонансного преобразователя // Приборы.- 2012. - . № 7. - с. 9 – 14.
5. Волков В.С., Баринов И.Н. Автоматизация разработки диагностического обеспечения интеллектуальных полупроводниковых датчиков давления // Приборы.- 2009. - № 12. - с. 20 – 26.
6. В.П. Фандеев, В.С. Волков Модели, методы и алгоритмы оптимизации диагностирования приборов.: Учебное пособие - Пенза: Изд-во ПГУ, 2007. – 76 с.
7. Тихонов А. И., Тихоненков В. А., Теория, расчет и основы проектирования датчиков механических величин: Учебное пособие.- Ульяновск: УлГТУ, 2000.-С 150-151.

References

1. Mokrov E.A., Barinov I.N., Cibizov P.N. Poluprovodnikovye p'ezochuvstvitel'nye jelementy mikrojelektronnyh datchikov davlenij. Osnovy proektirovanija i razrabotki: ucheb. posobie - Penza: Izd-vo Penz. gos. un-ta, 2009. - 104 s.
2. Barinov I.N., Cypin B.V. Sostojanie razrabotok i tendencii razvitija vysokotemperaturnyh tenzorezistivnyh datchikov davlenij na osnove karbida kremnija // Pribory i sistemy. Upravlenie, kontrol', diagnostika.−2010.− №11.−S. 50-60.
3. Volkov V.S., Barinov I.N. Ispol'zovanie sistemy Simulink pri imitacionnom modelirovanii vysokotemperaturnyh poluprovodnikovyh datchikov davlenija // Pribory.- 2011. - . № 7. - s. 50 – 55.
4. Volkov V.S., Barinov I.N. Poluprovodnikovye datchiki davlenija na osnove rezonansnogo preobrazovatelja // Pribory.- 2012. - . № 7. - s. 9 – 14.
5. Volkov V.S., Barinov I.N. Avtomatizacija razrabotki diagnosticheskogo obespechenija intellektual'nyh poluprovodnikovyh datchikov davlenija // Pribory.- 2009. - № 12. - s. 20 – 26.
6. V.P. Fandeev, V.S. Volkov Modeli, metody i algoritmy optimizacii diagnostirovanija priborov.: Uchebnoe posobie - Penza: Izd-vo PGU, 2007. – 76 s.
7. Tihonov A. I., Tihonenkov V. A., Teorija, raschet i osnovy proektirovanija datchikov mehanicheskih velichin: Uchebnoe posobie.- Ul'janovsk: UlGTU, 2000.-S 150-151