DETERMINATION OF THE SAFETY FACTOR FOR STATICALLY INDETERMINATE BEAMS OF VARIABLE SECTION
Овсянников М.Ю.1, Кузнецова С.Г.2
1Студент 4 курса,
2кандидат технических наук, доцент,
Пермский национальный исследовательский политехнический университет
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ЗАПАСА ПРОЧНОСТИ ДЛЯ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ БАЛОК ПЕРЕМЕННОГО СЕЧЕНИЯ
Аннотация
Проектирование строительных конструкций необходимо производить с использованием коэффициента запаса прочности, который учитывает случайные изменения нагрузки, дефекты конструкций при изготовлении, транспортировке и монтаже, неточности расчетов, связанные с упрощениями, неопределенными условиями и др. Для пластичных материалов коэффициент запаса определяется как отношение предельно допустимого напряжения – пределу текучести к максимальному напряжению, полученному при расчете.
Ключевые слова: коэффициент запаса прочности, составная неразрезная балка переменного сечения, метод сил, уравнение трех моментов, предельно допустимые напряжения.
Ovsyannikov M.Y.1, Kuznetsova S.G.2
14rd year student,
2PhD in technics, associate professor,
Perm National Research Polytechnic University.
DETERMINATION OF THE SAFETY FACTOR FOR STATICALLY INDETERMINATE BEAMS OF VARIABLE SECTION
Abstract
Structural engineering must be made using safety factor taking into account the random variation of the load, construction defects during manufacture, transportation and assembly, inaccuracy in the calculations associated with the simplifications, uncertain conditions, and others. For ductile materials, the safety factor is defined as the ratio of the maximum allowable stress - yield stress to the maximum voltage, resulting in the calculation.
Keywords: safety factor, composite continuous beam of variable section, work method, equation of three moments, allowable stress.
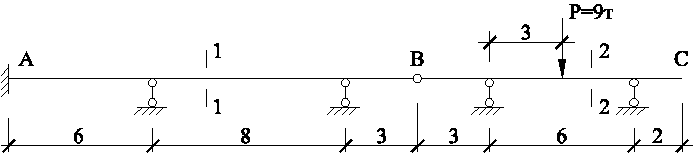
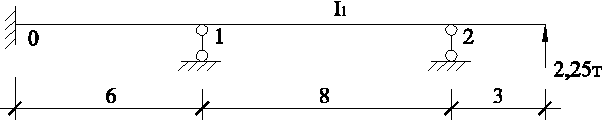
Определим коэффициент запаса прочности в балке переменной жесткости, показанной на рис. 1, если σпр=2400 кгс/см2.
Рис. 1 - Составная балка переменного сечения
Левая часть балки А-В (сечение 1-1) выполнена из I № 27а. Правая часть В-С (сечение 2-2) – из I № 33а.
Для решения задачи используем метод сил и уравнение 3-х моментов [1].
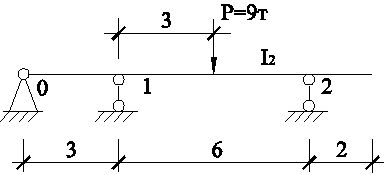
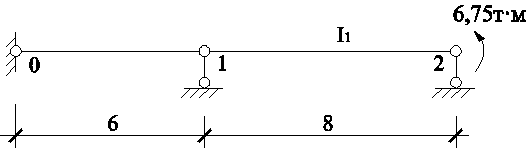
Рассмотрим правую часть составной балки В-С (рис. 2) – передаточную балку. nст = 1.
Рис. 2 - Передаточная балка В-С
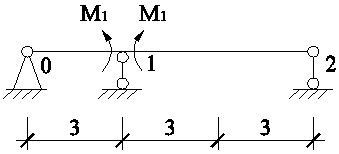
Основная система метода сил изображена на рис. 3.
Рис. 3 - Основная система метода сил для балки В-С
Составим уравнение трех моментов относительно опоры № 1:
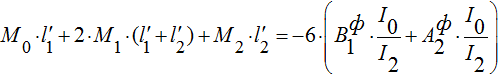(1)
где 
;
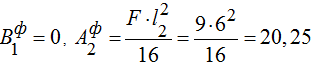, тс м2 – левый и правый углы поворота сечений балки от нагрузки;
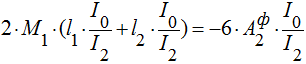, (2)
,
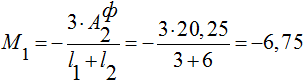т м (3)
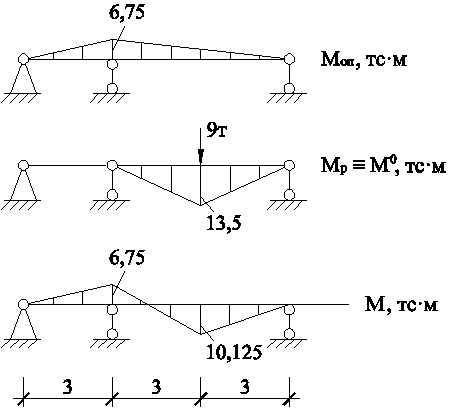
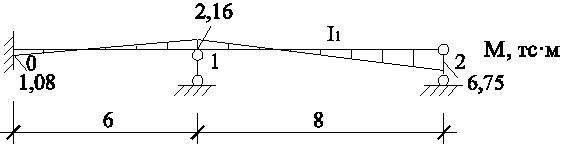
Построим эпюру изгибающих моментов М = Моп + Мр балки В-С:
Рис. 4 - Эпюра изгибающих моментов балки В-С
Рассмотрим левую часть составной балки А-В (рис. 5) – основную балку. На основную балку давление переносится с передаточной балки в шарнире В. nст = 2.
Рис. 5 - Основная балка А-В
Основная система метода сил изображена на рис. 6.
Рис. 6 - Основная система метода сил для балки A-B
Эпюру моментов (рис. 7) построим, используя метод моментных фокусных отношений. Достаточно знать левые моментные фокусные отношения
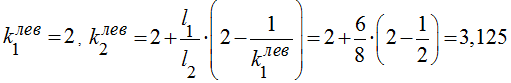(4)
Тогда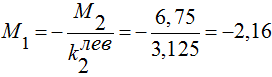 
тс м, (5)
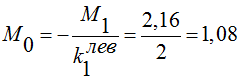тс м (6)
Рис. 7 - Эпюра изгибающих моментов балки А-В
Окончательная эпюра изгибающих моментов изображена на рис. 8.
Рис. 8 - Окончательная эпюра изгибающих моментов
Максимальные напряжения в балках:
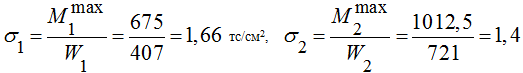тс/см2, тс/см2 (7)
Коэффициенты запаса:
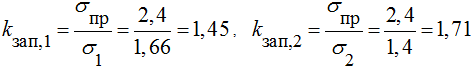, (8)
Балка удовлетворяет условию прочности 
. При этом коэффициент запаса прочности составил 
[2].
Литература
- Дарков А.В., Шапошников Н.Н. Строительная механика.: Учеб. для строит. спец. вузов. – 8-е изд., перераб. и доп. – М.: Высш. шк., 1986. – 607 с.
- Дарков А.В., Шпиро Г.С. Сопротивление материалов: Учебник для вузов. Изд. 4-е. «Высш. Школа», 1975. – 654 с.
References
- DarkovA.V., ShaposhnikovN.N. Stroitel'najamehanika.: Ucheb. dljastroit. spec. vuzov. – 8-eizd., pererab. idop. – M.: Vyssh. shk., 1986. – 607 s.
- Darkov A.V., Shpiro G.S. Soprotivlenie materialov: Uchebnik dlja vuzov. Izd. 4-e. «Vyssh. Shkola», 1975. – 654 s.