STRESSES IN BENDED TUBE AND FIBER REINFORCED CONCRETE ELEMENTS
Панченко Л.А.1, Серых И.Р.2, Юрьев А.Г.3
1Кандидат технических наук, доцент,
2Кандидат технических наук, доцент,
3Доктор технических наук, профессор,
Белгородский государственный технологический университет им. В.Г.Шухова
НАПРЯЖЕНИЯ В ТРУБОФИБРОБЕТОННЫХ ИЗГИБАЕМЫХ ЭЛЕМЕНТАХ
Аннотация
Изложены основы расчета изгибаемых трубофибробетонных элементов. Предусмотрена труба из полимеров, армированных стеклянными или углеродными волокнами. Эти же волокна используются для армирования бетонного ядра. Выведены формулы напряжений в ядре и трубе.
Ключевые слова: трубофибробетон, изгибаемый элемент, нормальные напряжения.
Panchenko L.A.1, Serych I.R.2, Yuriev A.G.3
1Candidate of Technical Sciences, docent,
2Candidate of Technical Sciences, docent,
3Doctor of Technical Sciences, professor,
Belgorod State Technological University named after V.G. Shukhov
STRESSES IN BENDED TUBE AND FIBER REINFORCED CONCRETE ELEMENTS
Abstract
The paper reports on calculation bases of bended tube and fiber reinforced concrete elements. The tube from fiber reinforced polymer is provided for. The same glass and carbon fibers are used for concrete kernel reinforcing. The formulas for stresses in kernel and tube were formulated.
Keywords: tube and fiber reinforced concrete, bended element, normal stress.
Трубобетон представляет собой композиционный материал, для которого довольно трудно построить математическую модель, например, установить эффект обоймы в результате расчета по методу конечных элементов. Поэтому важную роль при его изучении играют экспериментальные исследования.
Основной причиной повышенной прочности бетона в трубе является его боковое обжатие, препятствующее развитию растяжения в поперечном направлении. Повышение несущей способности трубобетонного элемента обеспечивается как за счет прочности характеристик бетона ядра, так и за счет композиции оболочки. Надо полагать, что оптимальное решение предусматривает одновременный рост процесса микротрещинообразования и разрушения бетона ядра и предельное состояние материала оболочки.
Экспериментальные исследования показывают, что в заполненных бетоном стальных трубах наблюдается довольно слабое сцепление между бетоном и оболочкой. Существуют две причины такого явления. Во-первых, бетон в большом диапазоне напряжений имеет меньший коэффициент Пуассона, чем сталь, и, следовательно, отделяется от трубы, когда оба материала испытывают продольную деформацию. Во-вторых, усадка бетона вызывает расслаивание на границе контакта двух материалов при любом нагружении. В результате выход из строя трубобетонных элементов вызывается отдельными факторами (текучестью стали, дроблением бетона) [1, 2].
Эти недостатки преодолеваются использованием полимеров, армированных волокнами, то есть устройством стеклопластиковой или углепластиковой обоймы. Увеличение прочности бетона достигается фибровым армированием. Получили распространение стеклянные и углеродные волокна.
Поскольку сжатые элементы с такого рода ядром и обоймой подробно рассмотрены в работе [3], остановим внимание на изгибаемых элементах.
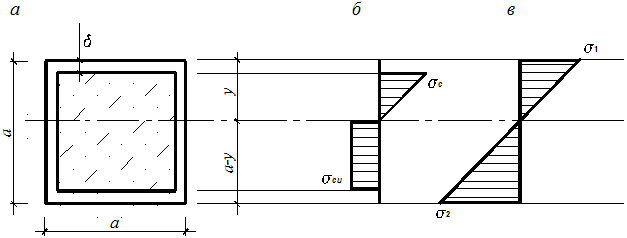
В качестве исследуемого объекта выберем балку на двух шарнирных опорах, несущую симметричную нагрузку в виде двух сосредоточенных сил, то есть имеющую область чистого изгиба. Обоймой служит труба квадратного сечения (рис. 1,а).
Существует приближенное представление, основанное на упрощенном предположении формы эпюры нормальных напряжений в растянутой зоне балки после образования трещин. На рис. 1,б показана эпюра напряжений, типичная для цементоволокнистого композита в раннем возрасте после образования трещин, когда при постоянной нагрузке волокна растягиваются или вытягиваются сквозь трещины по всей растянутой области. Предел прочности на растяжение после образования трещин вычисляется по формуле (2.13) [3], а есть напряжение сжатия на другой стороне балки. На рис. 1,в представлена эпюра напряжений в обойме, материал которой подчиняется закону Гука вплоть до разрушения.
Рис. 1 - Напряжения в изгибаемом трубофибробетонном элементе:
а – поперечное сечение; б – эпюра напряжений в фибробетоне; в – эпюра напряжений в обойме
Используя гипотезу плоских сечений, установим зависимости между напряжениями ![]()
![]() и (
и (![]() ):
):
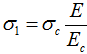 (1)
(1)
![]() , (2)
, (2)
где E – модуль продольной упругости материала обоймы; ![]() – модуль деформации фибробетона; y – расстояние от нейтральной оси до верхнего волокна сечения.
– модуль деформации фибробетона; y – расстояние от нейтральной оси до верхнего волокна сечения.
Для определения неизвестных y и ![]() используем уравнения равновесия:
используем уравнения равновесия: ![]() , то есть
, то есть
![]() (3)
(3)
![]() (4)
(4)
где М – изгибающий момент в сечении балки.
При записи формул (3) и (4) в связи с тем, что , допущены упрощения, существенно не влияющие на точность расчета.
Если полученные напряжения или превышают их допускаемые величины, следует провести корректировку фибрового армирования соответственно материала ядра или материала обоймы.
За пределами области чистого изгиба балки имеют место поперечные силы и касательные напряжения, которые в данной работе не рассматриваются, как и нормальные напряжения на оси y.
Вариационная многопараметрическая задача оптимизации проектного решения может быть осуществлена на основе энергетического критерия [4]. К числу варьируемых параметров относятся размеры обоймы и механические характеристики используемых материалов.
Литература
- Стороженко Л.И. Трубобетонные конструкции. – Киев.: Будiвельник, 1978. – 80 с.
- Адамян И.Р. Напряженно-деформированное состояние сталебетонных брусьев прямоугольного поперечного сечения с составной обоймой при сжатии и изгибе: дис. канд. техн. наук. – Белгород, 2000. – 157 с.
- Панченко Л.А. Строительные конструкции с волокнистыми композитами. – Белгород: изд-во БГТУ, 2013. – 184 с.
- Юрьев А.Г. Вариационные принципы строительной механики. – Белгород: БелГТАСМ, 2002. – 90 с.
References
- Storozhenko L.I. Trubobetonnye konstruktsii. – Kiyev.: Budivelnik, 1978. –80 s.
- Adamyan I.R. Napryazhenno-deformirovannoye sostoyaniye stalebetonnykh brusyev pryamougolnogo poperechnogo secheniya s sostavnoy oboymoy pri szha-tii i izgibe: dis. kand. tekhn. nauk. – Belgorod, 2000. – 157 s.
- Panchenko L.A. Stroitelnye konstruktsii s voloknistymi kompozitami. – Belgorod: izd-vo BGTU, 2013. – 184 s.
- Yuryev A.G. Variatsionnye printsipy stroitelnoy mekhaniki. – Belgorod: BelGTASM, 2002. – 90 s.