INVESTIGATION OF CROSS STACKS ON THE PROCESS OF THEIR COOLING IN COLD STORAGE

Кабаков З. К.¹, Грибкова Ю. В.², Габелая Д. И.³ 

¹Доктор технических наук, ²Кандидат технических наук, ³Кандидат технических наук,

Череповецкий государственный университет

ИССЛЕДОВАНИЕ ВЗАИМНОГО ВЛИЯНИЯ ШТАБЕЛЕЙ НА ПРОЦЕСС ИХ ОХЛАЖДЕНИЯ НА ХОЛОДНОМ СКЛАДЕ

Аннотация

В статье представлена математическая модель, в которой учитывается тепловое влияние соседних штабелей на процесс охлаждения. На основе проведенного анализа установлено, что при оценке продолжительности охлаждения штабеля необходимо учитывать влияние геометрии штабеля и расстояния между соседними штабелями на степень экранирования излучения от рассматриваемого штабеля соседним штабелем.

Ключевые слова: математическая модель, продолжительность охлаждения, тепловое взамовлияние, сляб, штабель.

Kabakov Z. K.¹, Gribkova Y. V.², Gabelaya D. I.³

¹Doctor of Technical Sciences, ²Candidate of Technical Sciences, ³Candidate of Technical Sciences,

Cherepovets State University

INVESTIGATION OF CROSS STACKS ON THE PROCESS OF THEIR COOLING IN COLD STORAGE

Abstract

The paper presents a mathematical model, which takes into account the thermal influence of neighboring stacks on the cooling process. Based on the analysis found that in assessing the duration of the cooling stack is necessary to consider the influence of the geometry of the stack and the distance between adjacent stacks on the degree of radiation shielding from the considered stack adjacent stack.

Keywords: mathematical model, the duration of cooling, thermal influence in return, slab pile.

Складирование непрерывнолитых слябов на холодном складе с целью их дальнейшего охлаждения производится строго поплавочно в штабеля высотой не более 4 м. Рядовой металл охлаждается в штабелях до температуры не выше 60 °С. Продолжительность охлаждения штабеля зависит от многих факторов, которые не учитываются при обрваботке слябов на холодном складе. В частности, не учитывается взаимное тепловое влияние на процесс охлаждения штабелей.

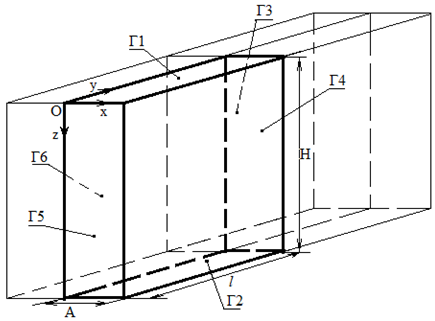
При построении модели предполагаем, что штабель формируется из слябов одной плавки и рассматривается сплошным телом. В силу симметрии охлаждения штабеля с боковых сторон будем рассматривать только ¼ часть штабеля (Рис. 1).

Рис. 1 - Схема выделенной расчетной области из рассматриваемого тела: А, ℓ– половина ширины и длины штабеля, соответственно, м, H – высота штабеля, м, Гi – поверхности, ограничивающие расчетную область, i =1..6

Температуру тела в начальный момент времени предполагаем неравномерной по ширине, высоте и длине штабеля. С учетом принятых допущений математическое описание тепловых процессов включает трехмерное уравнение теплопроводности в виде:

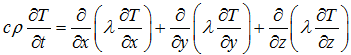                                                    (1)

заданное в области: 0 ≤ x ≤ A, 0 ≤ y ≤ l, 0 ≤ z ≤ H, 0 ≤ t ≤ t_k       (рисунок 1),

при начальном условии:

                                                                          (2)

и условиях на границах расчетной области (рисунок 1):

Г1, Г2, Г5:             (3)

Г4:                                         (4)

Г3, Г6:                                                                                              (5)

Здесь: λ = λ(Т)  - теплопроводность стали; ρ=ρ(Т)- плотность стали;  с = с(Т) – теплоемкость стали; t_к  - конечное время процесса; ε - степень черноты поверхности сляба; σ₀ - коэффициент излучения абсолютно черного тела; α_к - коэффициент теплоотдачи конвекцией; α_л - коэффициент теплоотдачи лучеиспусканием; Т_ср, T_п - температура окружающей среды и температура поверхности сляба;  – локальный угловой коэффициент переноса энергии эффективного излучения элементарной поверхности dF₁ на поверхность F₂.

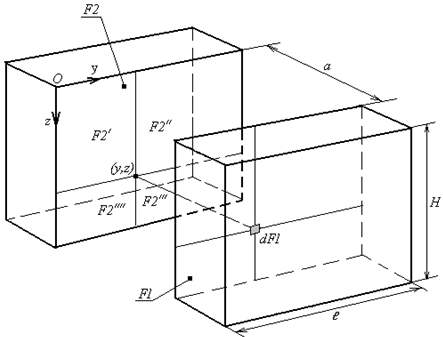
С помощью локального углового коэффициента излучения в формуле (4) учитывается влияние теплового излучения соседнего штабеля на процесс охлаждения рассматриваемого штабеля (Рис. 2).

Рис. 2 - Схема к расчету углового коэффициента  излучения от элементарной площадки dF₁ поверхности F₁ на поверхность F₂: а – расстояние между штабелями, 2ℓ, Н  - соответственно, длина и высота штабелей

Локальный угловой коэффициент  характеризует долю лучистой энергии от элемента площади dF₁ поверхности F₁ рассматриваемого штабеля, попадающей на поверхность F₂ соседнего штабеля, и которая при одинаковой температуре площадей экранируется площадью F₂ соседнего штабеля. В результате этого полное излучение площадки dF₁ уменьшается в  (1- ) раз (формула (4)).

Таким образом, коэффициент  соответствует степени экранирования излучения поверхности F₁ соседнего штабеля на поверхность F₂ рассматриваемого штабеля. При =0 (при ) экранирование отсутствует, а при =1 (при ) наступает полное экранирование.

Формула для расчета  получена с помощью методики, приведенной в работе [1]. В системе координат, приведенной на Рис. 2, она имеет вид:

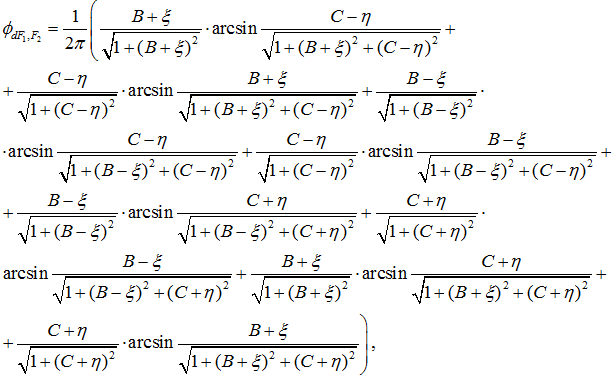(6)

где - относительные переменные, - относительные расстояния

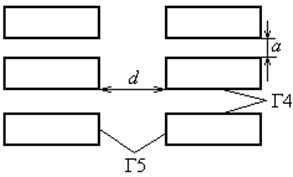
Используем формулу (6) для анализа степени экранирования в зависимости от геометрии рассматриваемого штабеля и расстояния до соседнего штабеля. Исследование выполнено для типичных размеров штабеля: высота штабеля H=2м, длина 2l=10м, ширина 2А=1м и расстояние между штабелями a=2м (Рис. 3).

Рис. 3 - Схема расположения штабелей (вид сверху)

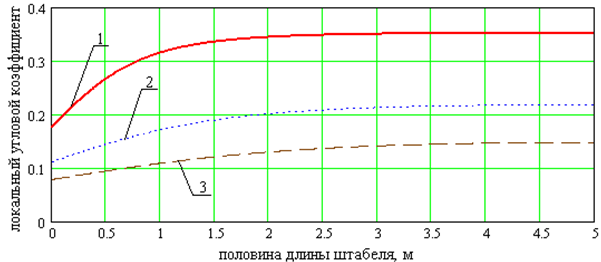
Рис. 4 - Распределение локального углового коэффициента φ_dF1,F2 по длине штабеля  (0 ≤ y ≤ l, при z =H/2) для различных расстояний между штабелями: 1 – a=1м,  2 – a=2м, 3 – a=3м

Результаты исследования приведены на Рис. 4 и 5 в виде зависимости  от половины длины штабеля (рисунок 4, при 0 ≤ y ≤ l и z = H/2 ) и от ширины торца штабеля (Рис. 5, при 0 ≤ x ≤ 2A и z = H/2) для различных значений расстояния между штабелями а.

Рис. 5 - Распределение локального углового коэффициента  φ_dF1,F2 (0 ≤ x ≤ 2A и z = H/2) для различных расстояний между штабелями:

1 – a=1м,  2 – a=2м, 3 – a=3м

На Рис. 4 и 5 видно, что с увеличением расстояния между поверхностями, находящимися в лучистом теплообмене, от a=1м до a=3м  распределение  становится более пологим. При этом максимальная величина коэффициента уменьшается более чем в 2 раза.

Для небольших расстояний между штабелями (a<1м) неравномерность  наблюдается только у края штабеля. В остальной части длины штабеля наблюдаются постоянные значения .

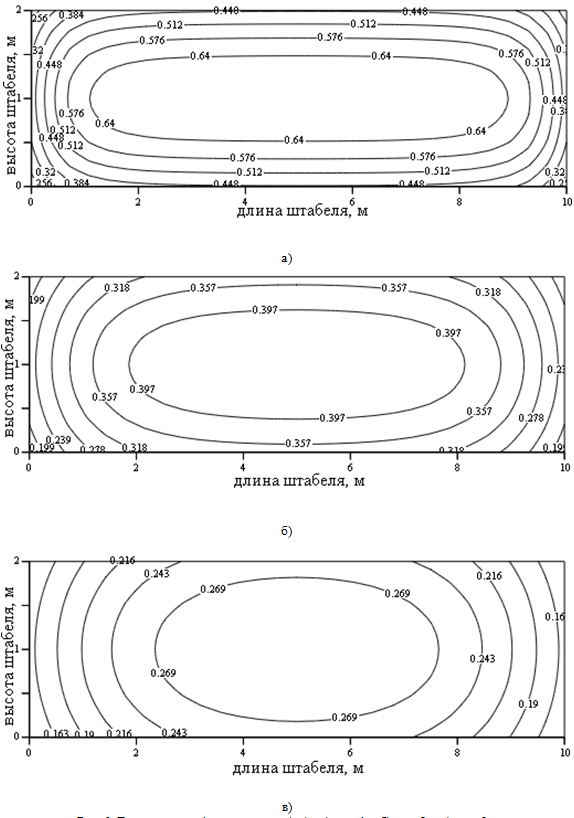
На рисунке 6 приведены линии уровня локального углового коэффициента  на поверхности Г4, соседней с Г4 другого штабеля.

Рис. 6. Линии уровня функции φ_dF1,F2(y,z)   а) – a=1м, б) – a=2м, в) – a=3м

Как видно на Рис. 6, степень экранирования () принимает наименьшее значение по краям боковой стороны штабеля. С увеличением расстояния зона неравномерности наблюдается в большей мере в районе узких сторон боковой поверхности.

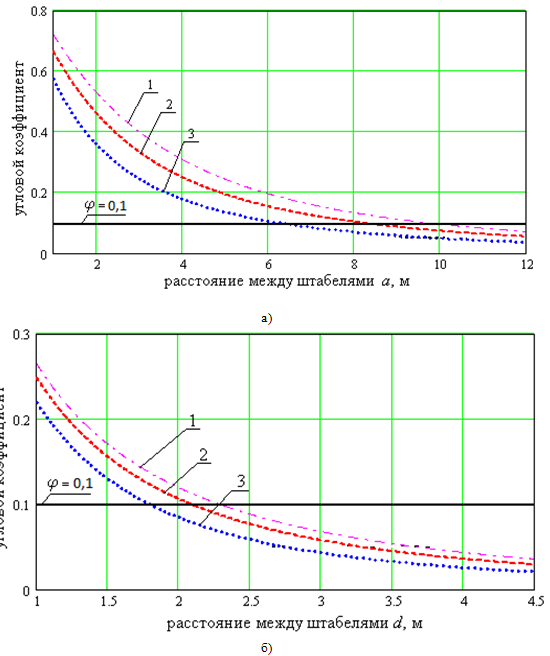
На Рис. 7 представлены результаты исследования величины доли лучистой энергии ( ), передаваемой от всей боковой поверхности Г4 на боковую поверхность соседнего штабеля (Рис. 7 а) и торца Г5 на торец соседнего штабеля (Рис. 7 б).

Рис. 7 - Зависимость доли лучистой энергии от расстояния: а) – между широкими гранями Н × 2l штабелей; б) – между торцевыми гранями Н × А штабелей; 1 - Н=4м, 2 - Н=3м, 3 - Н=2м; 2l =10м, А=0,7м

Из Рис. 7 можно оценить условия, при которых влияние соседних штабелей для их различных высот становится существенным (Таб. 1). Будем считать влияние существенным, если степень экранирования φ_F1,F2 ≥ 0,1. Результаты оценки условий существенного влияния соседних штабелей представлены в таблице 1.

Таблица 1

Н, м	Расстояние между штабелями
	Рис. 8 (а)	Рис. 8 (б)
2	a < 6,5 м	d < 1,7 м
3	a < 8,5 м	d < 2,1 м
4	a < 10,0 м	d < 2,3 м

В реальных условиях расстояние между соседними штабелями находится в пределах от 1 до 1,5 м, а значит тепловое взаимовлияние соседних штабелей будет существенным.

Система уравнений (1) - (5) решена численным методом конечных разностей с использованием явной схемы аппроксимации. Алгоритм расчета реализован в виде компьютерной программы.

Таким образом, разработана математическая модель, в которой учитывается тепловое влияние соседних штабелей на процесс охлаждения рассматриваемого штабеля. Выполнен анализ влияния геометрии штабеля и расстояния между соседними штабелями на степень экранирования излучения от рассматриваемого штабеля соседним штабелем.

Литература

1. Ключников А.Д., Иванцов Г.П. Теплопередача излучением в огнетехнических установках (инженерные решения задач). – М., 1970. – 400с.

References

1. Kluchnikov AD, GP Ivantsov Heat transfer by radiation in ognetehnicheskih installations (engineering problem solving). – M., 1970 - 400c.