STUDY OF ENERGY CONSUMPTION FOR THE TAKE-OFF OF A QUANTUM VEHICLE
STUDY OF ENERGY CONSUMPTION FOR THE TAKE-OFF OF A QUANTUM VEHICLE
Abstract
The prospect of introducing quantum vehicles using the thrust of a quantum engine-driver (QED) implemented in the pitch plane leads to the necessity to examine the specifics of energy consumption formation for the take-off of these vehicles. The mechanisms of energy input formation for the work of forces collinear to the longitudinal motion of the crew and the work of vertical forces providing the crew hovering are essentially different. In the absence of full-scale vehicles (FSVs) with QED, the study relies on software simulation modelling (SIM), flexible model and powerful software. The problem is the formation of a framework for analysing the energy cost of implementing the take-off of a quantum vehicle. The objectives of the development were: formation of algorithms for analysing energy costs of a quantum car; creation of the energy cost calculation subsystem (ECCS) in the author's Model of Quantum Vehicle Ground Motion (MQVGM); elaboration of the interface of interaction with the model; conducting SIM on the basis of MQVGM with experiments covering some set of variants of vehicle take-off. Methods. Development of the author's algorithm of take-off and hovering of the quantum car, implemented in the Simulink-modelling environment of the MQVGM. Formation of a trajectory framework of multiple take-offs on the basis of PIM processes of quantomobile take-off. Evaluation of energy efficiency of take-off realisations with the help of algorithmic and graphical capabilities of Matlab software. In a series of calculations of acceleration and suspension of the quantomobile under different scenarios of changing the angles of inclination of the trust vector, air resistance and lift force, rolling resistance on the supporting surface and other factors, an assessment of energy consumption for variants of the quantomobile take-off is given. Conclusion. The ECCS subsystem developed in the MQVGM environment allows to carry out a calculated study of energy consumption both for overcoming longitudinal forces of resistance to movement and for vertical suspension of the crew with ensuring its stability in the pitch plane. On the basis of calculations and their analyses carried out by means of MQVGM with ECCS, the cognitive complexity of formation of energy consumption of a quantum car at the stage of its take-off with their splitting by types of forces of resistance to motion has been overcome. MQVGM is regarded as a basis for further development of modelling of quantum car motion in arbitrary conditions.
1. Введение
На базе идей извлечения энергии из физического вакуума (ФВ) , , в физике рассматриваются концепции квантовых двигателей (КД), генерирующих траст (тягу) за счет целенаправленной деформации поля ФВ , . Примером могут служить разработки Леонова В.С. , . Надежда на практическую реализацию названых идей и концепций становится все более существенной , .
Реализация идеи КД приведет к появлению нового типа транспортных средств (ТС) – квантомобилей , , . Станет возможным прикладывать траст КД к корпусу экипажа непосредственно – без трансмиссии. Необходимость трансмиссии отпадет, колесам (при движении по опорной поверхности (ОП)) останется только опорная функция , .
При шарнирном обметании вектора траста в плоскости тангажа проявляется его вертикальная компонента, которую можно использовать для вертикального вывешивания – лифта квантомобиля (в роли трастовой подъемной силы – ТПС). Горизонтальная компонента траста при этом используется для преодоления сил сопротивления продольному движению экипажа , (здесь и везде далее используем слово «экипаж» в смысле «коляска», но не команда!). КД, с реализацией таким образом функций движителя ТС, становится силовой установкой типа Квантовый двигатель-движитель (КДД).
В рамках продольного движения квантомобиля в плоскости развёртывания угла тангажа β вектор траста FT раскладывается на две ортогональные компоненты FTx и FTz , :
В скалярной записи это:
В публикациях , , на базе авторской Модели приземного движения квантомобиля (МПДК) рассмотрена методика и даны примеры расчета тяговых сил квантомобилей для наземной среды движения ТС с возможным переходом в воздушную среду. Показывается, что расчетная методика, в связи с необходимостью учета лифта, отличается от традиционных алгоритмов расчета силового баланса автомобиля.
В работах , автором рассматривались вопросы продольной устойчивости квантомобиля.
В работах , обосновывались те требования к энергетической цене тяги (ЭЦТ) КДД, которые позволят квантомобилю превосходить современные ТС-аналоги по энергоэффективности. При этом было обусловлено разделение ЭЦТ на энергетическую цену горизонтальной тяги (ЭЦГТ) и энергетическую цену вертикальной тяги (ЭЦВТ).
Было отмечено, что размерность ЭЦТ, ЭЦГТ и ЭЦВТ: [Вт/Н] = [м/с] – суть размерность скорости. Именно с этой скоростью (что очевидно для горизонтального перемещения) энергия передается от мобильного объекта в среду движения . Это обуславливает простоту вычисления мгновенной мощности процесса горизонтального перемещения экипажа (произведение силы на скорость коллинеарного движения) и затем – работы и энергозатрат (интегрированием мощности по времени).
Для вертикального движения, особенно для вывешивания экипажа, всё не так просто – экипаж неподвижен, а энергия на висение затрачивается. В статье сформирована методика выработки требований к величине ЭЦВТ КД квантомобиля. Показано, что, например, для 10-тонного квантомобиля-грузовика ЭЦВТ должна быть менее 55 Вт/Н.
Взлёт объекта становится возможным только тогда, когда суммарная подъемная сила (СПС) (сумма аэродинамической и трастовой подъемных сил (АПС и ТПС)), превосходит вес этого объекта.
В статье показано, что с внедрением КДД в конструкцию ТС становится возможным моделирование взлета экипажа по единому алгоритму, охватывающему непрерывным образом все существующие способы (варианты) взлета ТС (от «самолетного» до «вертолетного»): CTOL, STOL и VTOL . Объединяющим фактором синтеза способов взлета в алгоритме является наличие у квантомобиля ТПС.
В работе также оценена динамика процессов, учет упругих сил и демпфирования в подвеске экипажа при взлете – это тоже сопровождается энергозатратами.
Затронутые аспекты, несомненно, должны найти место в анализе энергозатрат квантомобиля. Гипотезой исследования может быть следующее утверждение: при исследовании энергозатрат на взлет квантомобиля возможно расщепленное представление этих затрат по видам продольных и вертикальных составляющих траста и сил воздействия среды движения на экипаж – со сведением компонентных энергозатрат в их скалярную сумму.
2. Методы и принципы исследования
2.1. Цель и задачи исследования
Целью исследования явилось формирование структуры анализа энергозатрат на реализацию взлета квантомобиля.
Отсутствие признанных теоретических основ движения квантомобиля, натурных образцов исследуемых объектов и эмпирических данных по ним, вызывает необходимость использовать подход с опорой на программное имитационное моделирование (ПИМ).
Задачами по достижению цели являются:
1) формирование математической модели движения квантомобиля под поставленную цель;
2) разработка в авторской Simulink-модели приземного движения квантомобиля (МПДК) Подсистемы расчета энергозатрат (ПРЭ), позволяющей проведение исследования энергозатрат на различных фрагментах движения квантомобиля с детализацией составляющих по видам воздействия на экипаж в плоскости тангажа;
3) отработка интерфейса взаимодействия с моделью, задания сценариев взлета, контроль движения экипажа, многофакторного вывода результатов;
4) проведение ПИМ на базе Simulink-модели с экспериментами, охватывающими некоторое множество вариантов взлета ТС с оценкой компонентных и общих (суммарных) энергозатрат;
5) обсуждение и обобщение результатов расчетов;
6) формирование рекомендаций и выводов.
2.2. Балансы сил и моментов в 3-DOF модели приземного движения квантомобиля
Используем 3-DOF модель приземного движения квантомобиля (МПДК), развиваемую в авторских работах , , – учитываем балансы горизонтальных сил, вертикальных сил и моментов сил, действующих в плоскости тангажа.
Баланс горизонтальных сил, действующих на квантомобиль , :
где Fr – сила сопротивления качению опорных колес, Н;
Fwx – сила сопротивления воздуха продольному движению, Н;
Fax – продольная сила инерции экипажа, Н;
Gq' – сила давления экипажа на ОП с учетом частичного лифта, Н;
fk0 – коэффициент сопротивления качению колес при нулевой скорости;
fkv – скоростной коэффициент сопротивления качению колес, с2/м2;
Vq – скорость продольного движения квантомобиля, м/с;
cd – коэффициент продольного аэродинамического сопротивления;
ρw – плотность воздуха, Н ×с2/м4;
Sfr – фронтальная (лобовая) площадь экипажа, м2;
Gq – сила тяжести квантомобиля (Gq = m·g), Н;
g – ускорение свободного падения, м/с2;
ax – продольное ускорение экипажа, м/с2;
δwh – коэффициент инерции вращения опорных колес экипажа.
Сила Gq' = Gq – (FTz+Fwz) = Gq – FzSum, где Fwz – АПС, а FzSum – СПС. Для квантомобиля приведенная масса m’ = Gq(1+δwh)/g учитывает вращение только опорных колес (привод отсутствует).
Баланс вертикальных сил :
где Fup(z) – сила упругости подвески (меняющаяся по вертикальному ходу z);
Fам(vz) – сила сопротивления амортизаторов подвески (зависящая от скорости вертикального движения vz);
Fvpl(vz2) – сила воздушного сопротивления вертикальному движению экипажа (с учетом его площади в плане Spl);
Faz(az) – сила инерции, возникающая при вертикальном ускорении az.
С учетом того, что Fup(z) = Gq – z·cup, (где cup – приведенный коэффициент упругости (жесткости) подвески), можно записать:
Обозначив z·cup = Fpz и заметив, что это – высвободившаяся часть силы упругости, перешедшая в потенциал лифта, можем записать для силы, идущей на вертикальное ускорение экипажа:
где Fvz = Fам(vz) + Fvpl(vz2) – совокупность сил, связанных со скоростью вертикального движения экипажа.
В форме ДУ это:
где: kam – приведенный коэффициент демпфирования амортизаторов подвески, Н·с/м;
kwv = cdv ·(ρw/2)·Spl – фактор вертикальной обтекаемости экипажа, Нс2м–2;
cdv – аэродинамический коэффициент сопротивления вертикальному перемещению экипажа;
Spl – площадь в плане экипажа, м2.
Детали и особенности использования баланса вертикальных сил в МПДК можно почерпнуть из работы . Упомянем только, что система вертикальных перемещений экипажа учитывает три этапа: этап I с опорой на колеса (до высоты Hlf1) (конфигурация 1); этап II движения вывешенного над ОП экипажа с висящей подвеской (до высоты Hlf2) (все еще конфигурация 1), за ним этап III – с убранной подвеской и выдвинутым оперением (до высоты Hlf3) (конфигурация 2).
Баланс моментов сил усовершенствован на базе схемы рис. 1 (с профилем Davis), где обозначены: Vq – вектор скорости движения квантомобиля; V∞ – скорость невозмущенного набегающего потока воздуха (|V| = |V∞|); Cg – центр тяжести (ЦТ) экипажа; Gq – сила тяжести экипажа; Fa – приведенная сила инерции экипажа; CFT – точка приложения траста КД к корпусу экипажа; FT, FTx и FTz – сила тяги КД (траст) и ее покоординатные компоненты; Cw – центр давления (ЦД) аэродинамических сил; Fw, Fwx и Fwz – сила воздействия воздуха и ее покоординатные компоненты; Ff1 и Ff2 – силы сопротивления качению передних и задних колес, соответственно; Tf1 и Tf2 – моменты сопротивления качению колес; hFwx, hFTx, hg – расстояния векторов соответствующих сил Fwx, FTx, Fa от ОП; lFwz, lFTz – расстояния векторов соответствующих сил Fwz, FTz до вертикали от оси задних колес; l0 – расстояние вектора силы Fwz до вертикали центра колесной базы; Lwb, L1 и L2 – расстояния базовое и от осей колес до проекции центра тяжести на ОП; A и B – центральные точки пятен контакта колес с ОП; Rz1 и Rz2 – нормальные реакции ОП; Lst – расстояние между стабилизирующими трастерами (введено в настоящем исследовании).
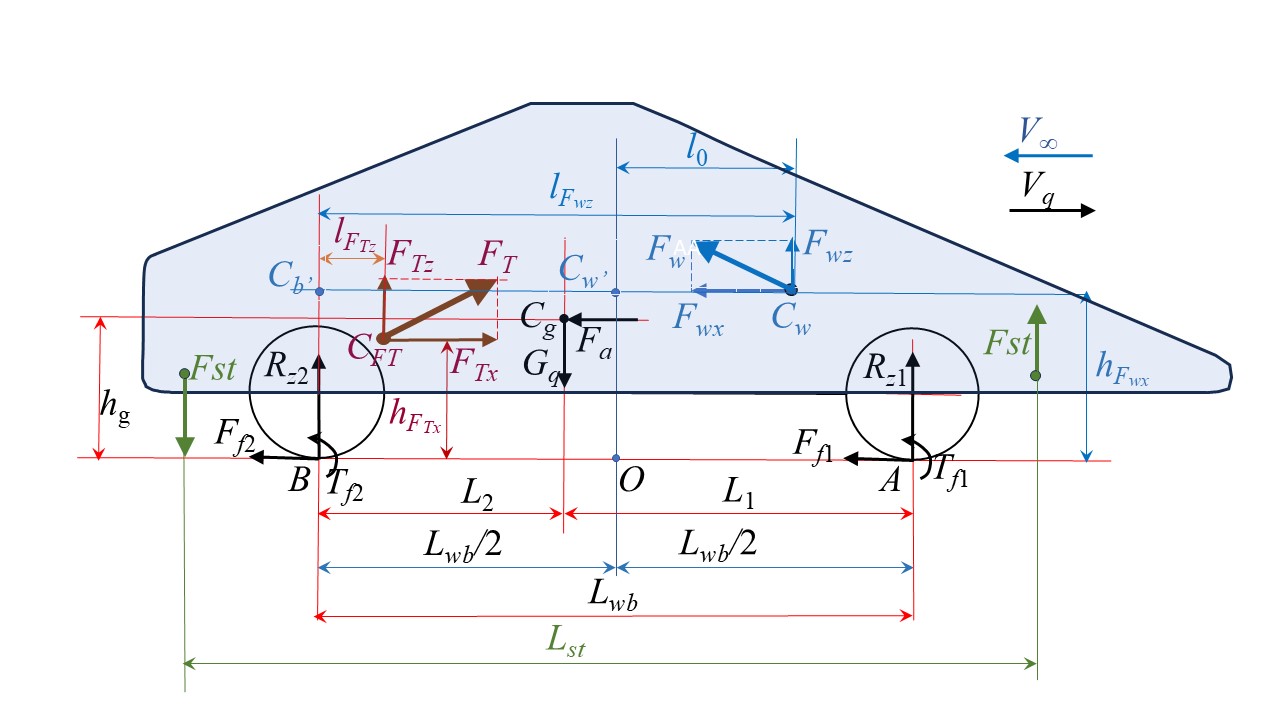
Рисунок 1 - Схема сил, формирующих балансы сил и моментов
Из него можно найти нормальную реакцию ОП Rz1. Аналогичное уравнение моментов относительно точки A позволяет найти реакцию Rz2. Опрокидывающий питч-момент MΣpm = Lwb(Rz1–Rz2)/2. Требуемый стабилизирующий момент (ТСМ) тогда равен Mst = –MΣpm.
Если условиться, что ТСМ будет реализован двумя дополнительными стабилизирующими трастерами, установленными на расстоянии Lst друг от друга (один на передке, другой на корме корпуса – см. рис. 1), то требуемая тяга каждого из них определится уравнением:
2.3. Мощности и энергозатраты в МПДК
Мощность реализации горизонтальных сил воздействия среды движения (СВСД), в соответствии с (3):
Напомним важное из работы : Vq – являясь скоростью горизонтального перемещения экипажа, одновременно характеризует скорость передачи энергии от мобильного объекта в среду движения.
Подъемные силы ТПС и АПС различаются по физической сути их формирования (и сопутствующих преобразовательных процессов): ТПС – феномен прямого контактного воздействия вертикальной компоненты траста КД на корпус ТС в точке приложения (либо возникновения) траста (ТПТ), а АПС – результат опосредованного (через форм-фактор корпуса ТС) вертикального воздействия воздушной среды на ТС, сфокусированного в его ЦД (в комбинации Fwz c Fwx ). Если ТПС зависит только от произвола управляющего сигнала и напрямую не зависит ни от профиля квантомобиля, ни от его скоростного и нагрузочного режимов, то АПС напротив – является функцией аэродинамического качества экипажа (Kаэр = cl/cd) и скоростного режима ТС.
Исходя из этого, мощность процесса реализации ТПС будет определяться посредством предопределенного («паспортного») ЭЦВТ КД, т.е. NFTz = FTz·KNFtz (где KNFtz = const не зависит от скорости ТС и верно даже для неподвижно висящего ТС).
Вид же мощности реализации АПС качественно иной: из равенства Fwz = Fwx·(cl/cd) (в обусловленном для модели диапазоне скоростей) следует
Можно даже записать:
В итоге мощность реализации СПС:
Поддержка ТСМ требует энергозатрат. Мгновенная мощность, реализуемая системой из двух трастеров, (несмотря на разнонаправленность их тяги), равна: NFst = 2·|Fst|·KNFst , где KNFst – ЭЦВТ стабилизирующего трастера ([Вт/Н]).
Компонентные энергозатраты определяются интегралами мощностей реализации рассмотренных сил по времени рассмотрения процессов. Общие энергозатраты определяются скалярной суммой компонентных энергозатрат.
2.4. Программное обеспечение МПДК
Структура имитационной системы представлена в . Она состоит из пяти подсистем: Vectored_Thrust – для выработки сценариев реализации во времени задающего вектора FT(t) и угла β(t); Longitudinal Dynamics – расчета показателей динамики продольного движения экипажа (см. , ); Reactions&Moments – расчета силовых моментов в плоскости тангажа (см. ); Vertical Dynamics – динамики вертикального движения экипажа (см. ); Energetics – расчета показателей энергетики движения (продвинута относительно ).
Отметим наличие множества дисплеев и осциллографов (в терминологии Simulink-Matlab) в подсистеме Energetics (рис. 2) – для детального анализа и вывода результатов расчетов.
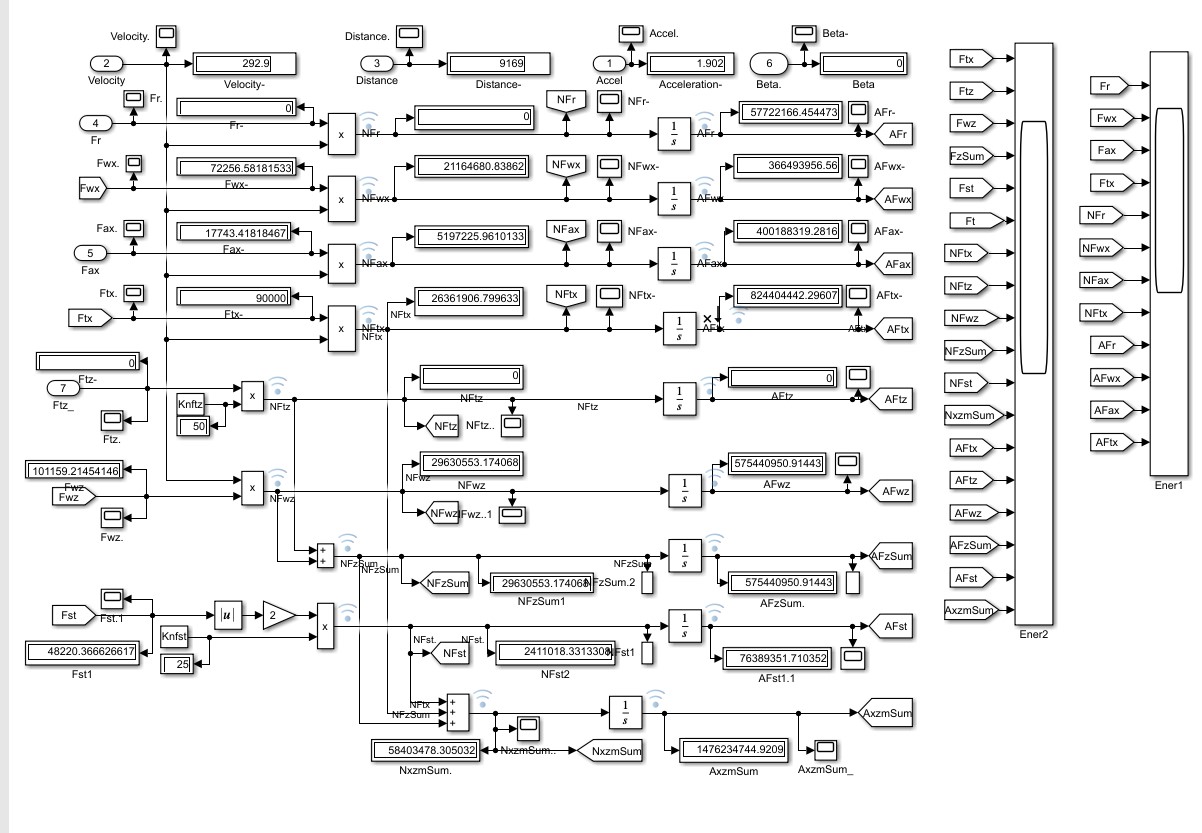
Рисунок 2 - Модуль ПРЭ Energetics
3. Результаты расчета показателей движения квантомобиля
3.1. Настройка моделей квантомобилей
Для отработки ПРЭ, а затем проведения ПИМ взлета квантомобиля привлекли две крайних макромодели из ряда «плохообтекаемых тел» (ПОТ) (bluff bodies) : 1-Box и Davis (ранее использованных автором в исследовании ). ПОТ 1-Box (с габаритами грузовика КамАЗ-4326), с низкими аэродинамическими свойствами (cd = 0,5; cl = 0; Каэр = cl/cd = 0 – т.е. с отсутствием АПС), в крайне тяжелых дорожных условиях (fk0 = 0,3). ПОТ Davis с превосходной аэродинамикой (cd = 0,263; cl = 0,42; Каэр = cl/cd = 1,6 – т.е. со значительной АПС) в крайне легких условиях горизонтальной ОП (fk0 = 0,02). Профили этих ПОТ представлены в .
В табл. 1 помещены основные параметры моделей. В ней L, W и H – габаритные длина, ширина и высота моделей, соответственно; Hg и Hw – высоты центра тяжести (ЦТ) и центра аэродинамического давления; rd – радиус колес. Sfr1 и Sfr2 – фронтальная (лобовая) площадь экипажа в наземном и в летном вариантах, м2; Spl1 и Spl2 – площадь в плане экипажа в наземном и в летном вариантах, м2.
Для обоих вариантов ПОТ приведенные параметры подвески: cup = 600000 Н/м, kam = 32000 Нс/м .
Таблица 1 - Основные данные по моделям 1-Box и Davis
Параметр | 1 | 2 |
1-Box | Davis | |
L, м | 7,3 | 7,3 |
W, м | 2,55 | 2,55 |
H, м | 3,3 | 1,87 |
Sfr1, м2 | 8,5 | 4,76 |
Sfr2, м2 | 8,5 | 5,5 |
Lwb, м | 4,25 | 4,87 |
L2, м | 2,125 | 2,435 |
Hg, м | 1,3 | 0,9 |
Hw, м | 1,46 | 1,0 |
rd, м | 0,5 | 0,5 |
m, кг | 8970 | 8970 |
Gq, Н | 87995,7 | 87995,7 |
FT, Н | 90000 | 90000 |
cd1 | 0,5 | 0,263 |
cd2 | 0,4 | 0,25 |
cl1 | 0 | 0,42 |
cl2 | 0,05 | 0,35 |
cm1 | 0 | –0,35 |
cm2 | –0,05 | –0,2 |
cdv1 | 0,8 | 0,6 |
cdv2 | 0,7 | 0,5 |
Spl1, м2 | 18 | 15 |
Spl2, м2 | 24 | 22 |
fk0 | 0,3 | 0,02 |
fkv, с2/м2 | 0,00037 | 0,00037 |
Lst, м | 7 | 7 |
KNFtz, Bт/Н | 50 | 50 |
KNFst, Bт/Н | 25 | 25 |
ЦТ обеих моделей расположили в их срединных плоскостях колесной базы (L2=Lwb/2, где Lwb – колесная база, а L2 – расстояние от ЦТ до вертикальной плоскости задней оси). Точку приложения траста расположили в ЦТ.
Значения ЭЦВТ установили на основе обработки данных исследований , , , и др., обобщенных автором в работе : для тягового трастера КД KNFtz = 50 Bт/Н; для стабилизирующего трастера – KNFst = 25 Bт/Н.
В целях обеспечения возможности продольного движения экипажа весом 88 кН при его полном вывешивании выбрали траст FT = 90 кН (обосновано в , ). Во всех расчетных реализациях взлета рост траста с нуля до 90 кН происходит за 5 секунд.
3.2. Расчетные действия
Для мелких серийных графиков с отсутствующими размерностями по осям (на рис. 4 ÷ 8) установили следующие размерности величин: для сил Fr, Fwx, Fax, FTx, FTz, Fwz, FzSum, Fst, FT – Н; для мощностей NFr, NFwx, NFax, NFTx, NFTz, NFwz, NFzSum, NFst, NxzmSum – Вт; для энергозатрат AFr, AFwx, AFax, AFTx, AFTz, AFwz, AFzSum, AFst, AxzmSum – Дж. Ось времени – в с. При обсуждении результатов расчетов конкретика размерностей может меняться. NxzmSum и AxzmSum – суммарные мощность и энергозатраты (скалярные суммы компонентных показателей).
Расчетные действия начали с построения графиков изменения вертикальной координаты pz взлета ПОТ 1-Box и Davis при FT = 90 кН и различных углах наклона вектора траста β – рис. 3. На этом рисунке для угла β = 77,9° показаны значения времени подъема экипажей t10м и t25м на высоты Hlf2 = 10 м и Hlf3 = 25 м, соответственно.
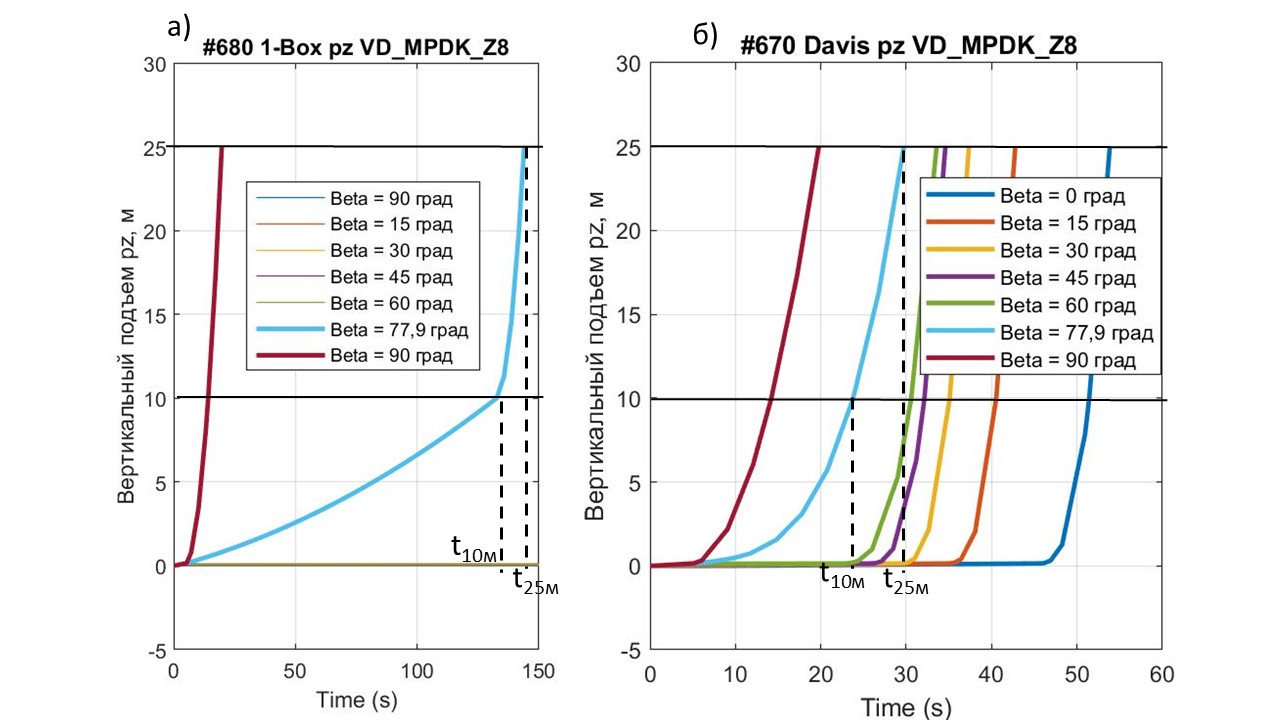
Рисунок 3 - Графики изменения координаты pz взлета ПОТ при FT = 90 кН и различных углах наклона вектора траста β:
а - 1-Box; б - Davis
Затем рассмотрели в деталях (реализация сил, мощностей и энергозатрат) лифт до высоты Hlf3 = 25 м с приложением к ПОТ вертикально направленного траста, без горизонтального движения экипажа (FT = 90 кН, β = 90°) – рис. 4.
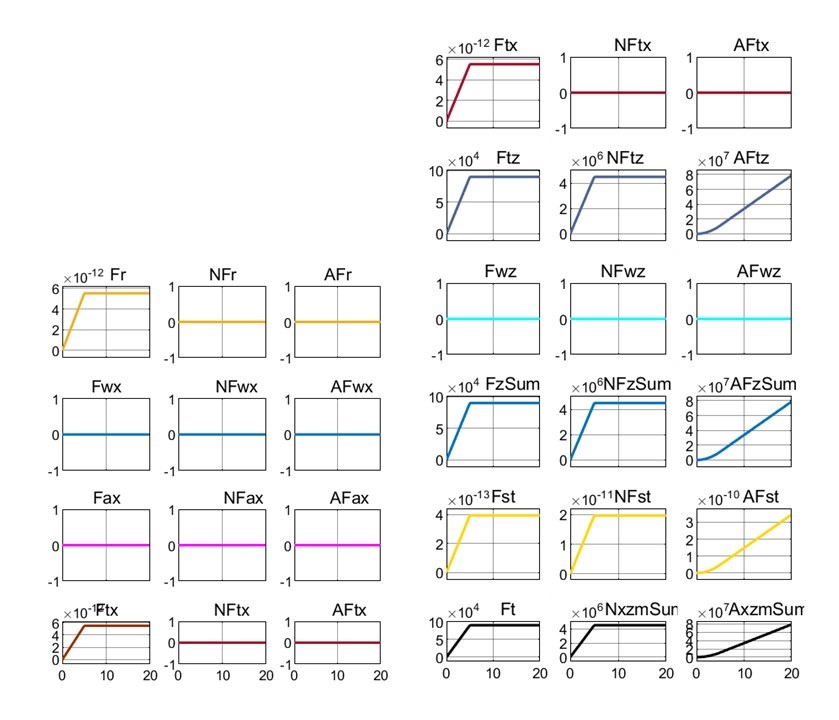
Рисунок 4 - Реализация сил, мощностей и энергозатрат при взлете модели 1-Box под воздействием траста FT = 90 кН и β = 90° до высоты Hlf3 = 25 м
На рис. 5 отображена реализация сил, мощностей и энергозатрат при взлете модели 1-Box под воздействием траста FT = 90 кН и β = 77,9° до высоты Hlf3 = 25 м.
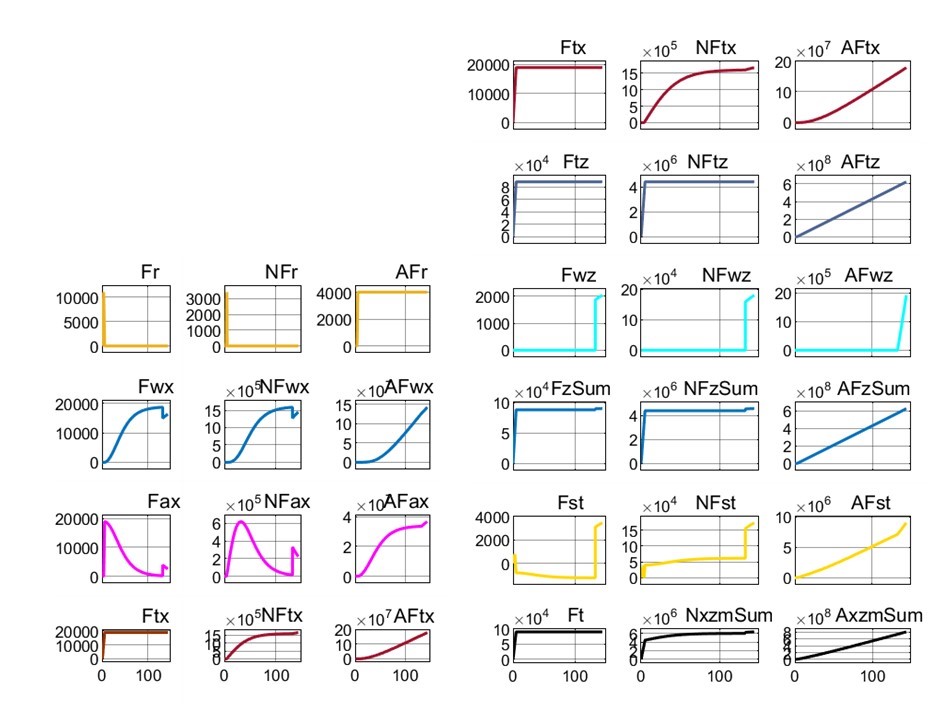
Рисунок 5 - Реализация сил, мощностей и энергозатрат при взлете модели 1-Box под воздействием траста FT = 90 кН и β = 77,9° до высоты Hlf3 = 25 м
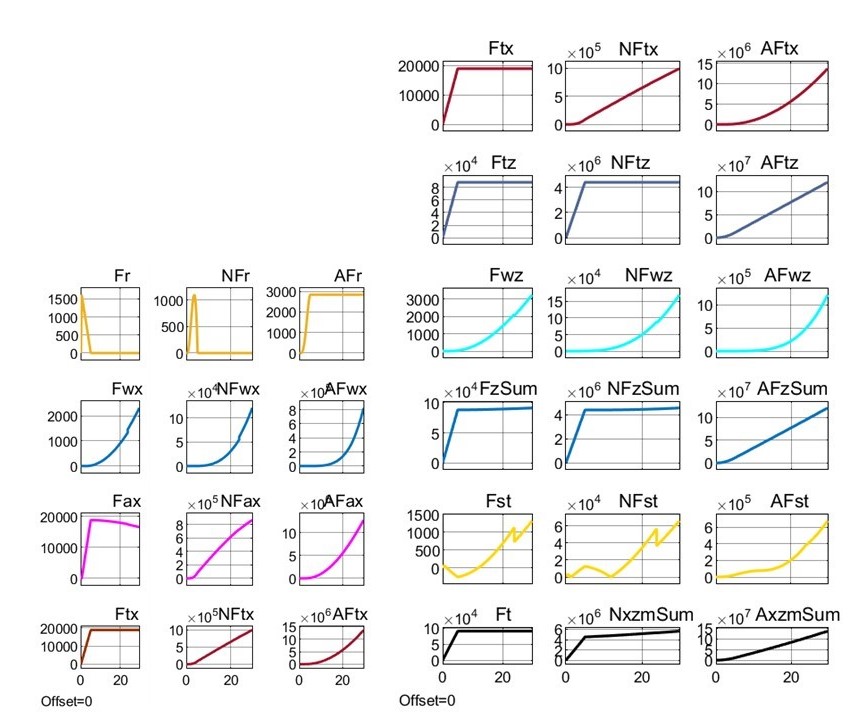
Рисунок 6 - Реализация сил, мощностей и энергозатрат при взлете модели Davis под воздействием траста FT = 90 кН и β = 77,9° до высоты Hlf3 = 25 м
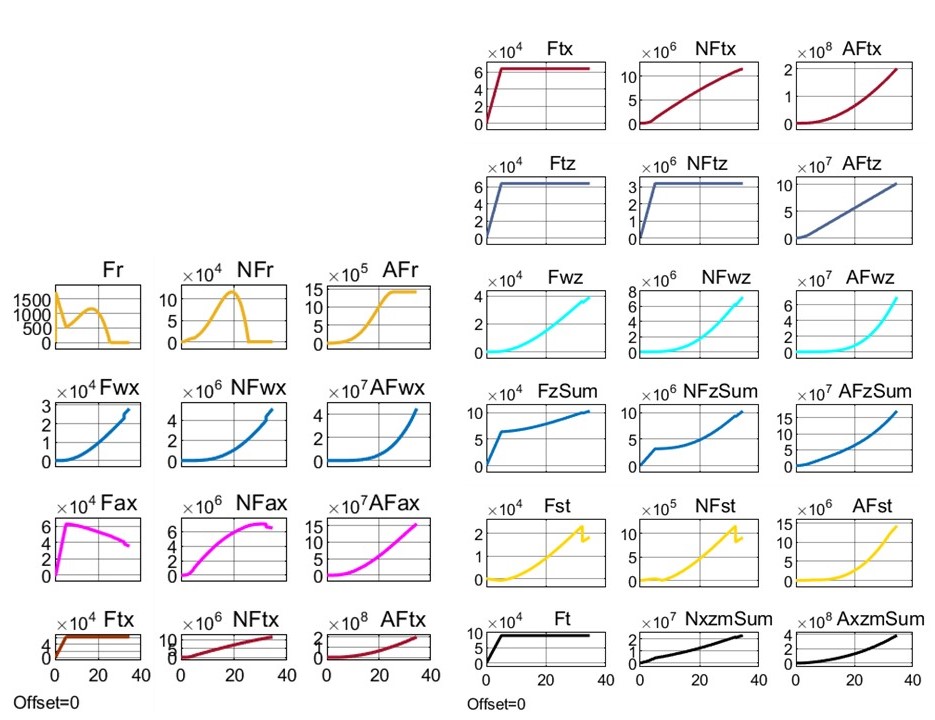
Рисунок 7 - Реализация сил, мощностей и энергозатрат при взлете модели Davis под воздействием траста FT = 90 кН и β = 45° до высоты Hlf3 = 25 м
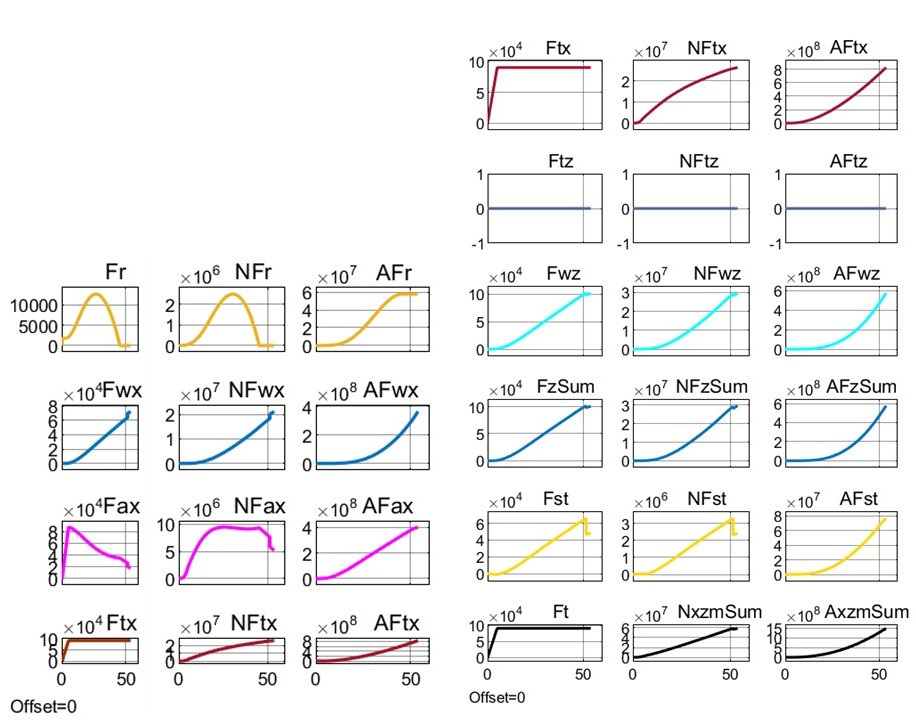
Рисунок 8 - Реализация сил, мощностей и энергозатрат при взлете модели Davis под воздействием траста FT = 90 кН и β = 0° до высоты Hlf3 = 25 м
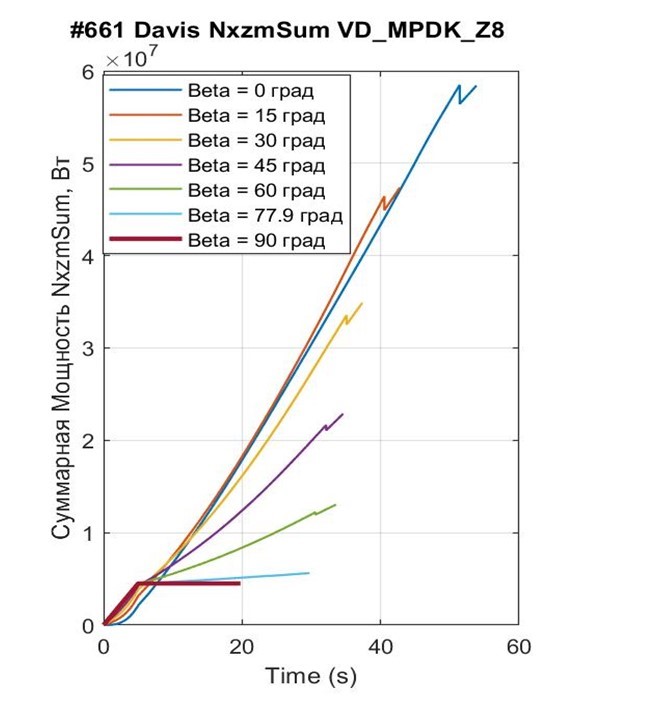
Рисунок 9 - Реализация суммарной мощности NxzmSum при взлете модели Davis под воздействием траста FT = 90 кН и β = 0° ÷ 90° до высоты Hlf3 = 25 м
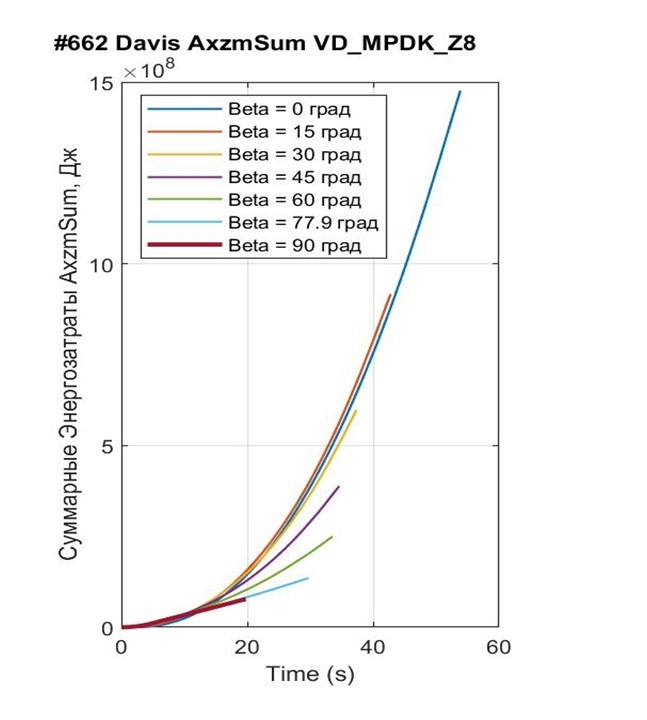
Рисунок 10 - Реализация суммарных энергозатрат AxzmSum при взлете модели Davis под воздействием траста FT = 90 кН и β = 0° ÷ 90° до высоты Hlf3 = 25 м
4. Обсуждение результатов расчетов
4.1. Сравнение энергозатрат 1-Box и Davis
Анализ графиков изменения координаты pz взлета ПОТ 1-Box и Davis на рис. 3 показал существенную разницу между этими крайними по профилю и нагруженности вариантами ПОТ. Отсутствие АПС Fwz у ПОТ 1-Box (при cl = 0) и всего лишь двухпроцентный запас тяги траста FT над весом экипажа Gq (90 кН против 88 кН) обусловили возможность отрыва колес этого экипажа от ОП лишь при углах β = 77,9° ÷90° (см. рис. 3.а). Более эффективные подъемы с расширением диапазона значений угла β, естественно, будут происходить при тяге траста FT > 90 кН. Однако ограничились в данном исследовании FT = 90 кН – достаточной величиной траста для выявления отличий энергозатрат сравниваемых вариантов движения частично вывешенного квантомобиля.
Как отмечалось, при β = 90° темп подъема сравниваемых ПОТ мало чем отличается (t25 = 19,94 для 1-Box и t25 = 19,90 для Davis) – это объясняется отсутствием АПС при vx ≈ 0 также и у Davis; и весьма малым влиянием разницы конфигураций экипажей в плане (Spl и cdv) при малых вертикальных скоростях vz. При вертикальном взлете, естественно, NFTx= 0, AFtx= 0 (см. рис 4); NFst = 0, AFst = 0 (поскольку силы Gq, FTz приложены в ЦТ, а FTx = 0). Реализуемая суммарная мощность NxzmSum = NFzSum = 4500 кВт, а энергозатраты на подъем до высоты 25 м (зависящие в данном случае только от ЭЦВТ) AxzmSum = AFzSum = 78 588 кДж (у 1-Box), 78 482 кДж – у Davis.
Таблица 2 - Показатели сил, мощности и энергозатрат ПОТ 1-Box и Davis на финишный момент взлета t25 на высоту 25 м под воздействием траста Ft = 90 кН при различных углах его наклона β
Динамика и энергетика взлета при β = 77,9° для сравниваемых ПОТ уже значительно отличается – см. рис. 3; варианты 2 и 4 в табл. 2; сравни также рис. 5 и 6. Время взлета для 1-Box t25 = 144 c, а для Davis t25=29,7 с.
Сравнивая, например, для β = 77,9° рис. 5 (1-Box) и рис.6 (Davis), можно отметить следующее:
1) при одинаковой и постоянной горизонтальной силе тяги FTx=18,86 кН характер изменения мгновенной мощности NFTx и реализуемые её значения существенно отличаются;
2) значения совершенной этой силой работы AFTx до выхода на высоту 25 м отличаются на порядок: 178 450 кДж у 1-Box и 13 647 кДж у Davis.
Проведем анализ отличий компонентных сил, мощностей и энергозатрат ПОТ 1-Box и Davis при взлете на высоту 25 м под воздействием траста Ft = 90 кН при угле его наклона β = 77,9° (см. рис. 5 и 6, также варианты 2 и 4 в табл. 2).
Сила сопротивления качению колес Fr = 0 почти на всей дистанции разгона для обоих ПОТ (экипаж вывешен вместе с колесами), за исключением силового пика и энергозатрат на реализацию силы страгивания экипажа с места (см. AFr = 4 кДж и AFr = 2,8 кДж в табл. 2).
Характер изменения сил фронтального сопротивления воздуха Fwx существенно отличается (см. рис. 5 и 6) и к тому же на разных дистанциях разгона для ПОТ приводят к значительной разнице энергозатрат (AFwx = 141 838 кДж и AFwx = 836,2 кДж в табл. 2).
Энергозатраты на преодоление сил инерции прямо связаны с конечной скоростью ускоренного разбега (см. vx= 88,6 и 52,4 м/с в табл. 2), и зафиксированы на уровне AFax = 36 608 кДж и AFax = 12 818 кДж.
В результате при FTx = Fr + Fwx + Fax = 18.86 кН для обоих ПОТ, энергозатраты AFtx на горизонтальное перемещение при взлете до 25 м: для 1-Box 178 450 кДж, для Davis 13 647 кДж.
Энергозатраты на висение экипажа при силе вывешивания экипажа (ТПС) FTz =
88кН и обеспечивающей её мощности NFTz = 4 400 кВт (при KNFtz = 50 Вт/Н) напрямую зависят от времени висения (t25 за минусом времени от начала разбега до отрыва колес). Эти затраты равны 632 342 кДж и 119 815 кДж.
Энергозатраты на обеспечение АПС Fwz равны 1 927 кДж и 1 215 кДж, причем для 1-Box эти затраты связаны только со вторым («лётным») профилем (на высотах от 10 до 25 м).
В величине FzSum = FTz + Fwz в данных примерах (при Gq = 88 кН и Ft=90 кН) составляющая FTz определяет в основном динамику вывешивания экипажа до отрыва колес от ОП, а Fwz – динамику дальнейшего взлета (см. ). Энергозатраты зависят от времени висения t25.
Противоположно направленные силы Fst (см. рис. 1), непрерывно меняющие свою величину (компенсируя динамический питч-момент) и этим обеспечивающие постоянную стабилизацию экипажа в процессе взлета (см. рис. 5 и 6), требуют энергозатрат на динамическую реализацию этой пары сил (при KNFst = 25 Вт/Н) 8 993 кДж и 677 кДж (см. табл. 2).
В итоге суммарные энергозатраты на взлет (AFxzmSum = AFTx + AFzSum + AFst) при β = 77,9 ° до 25 м ПОТ 1-Box составили 811 712 кДж, а на взлет Davis – 135 354 кДж, т.е. с шестикратной разницей
4.2. Оценка энергозатрат Davis для различных стратегий взлета
Оценим энергозатраты взлета ПОТ Davis на высоту 25 м под воздействием траста FT = 90 кН при нескольких постоянных углах его наклона β – привлекаем данные табл. 2, варианты 3 ÷ 6.
Видим, что с уменьшением угла наклона β (90° – 77, 9° – 45° – 0°) время взлета t25 увеличивается (19,9 – 29,7 – 34,6 – 53,8), финишная продольная скорость vx увеличивается (0 – 52,4 – 182 – 293), горизонтальный путь sx увеличивается (0 – 725 – 3178 – 9169), что естественно. Как следствие, энергозатраты на преодоление горизонтальных сил сопротивления FTx увеличиваются (0 – 13647 – 201831 – 824404 кДж), функция энергозатрат на вывешивание и поддержку висения ТПС FTz имеет выпуклый характер (78482 – 119815 – 102098 – 0 кДж), энергозатраты на АПС Fwz увеличиваются (0 – 1215 – 69715 – 575441 кДж), энергозатраты на стабилизацию экипажа Fst увеличиваются (0 – 677 – 14370 – 76389 кДж), суммарные энергозатраты на взлет FxzmSum увеличиваются (78 482 – 135 534 – 388 014 – 1 476 235 кДж).
Факт того, что сценарии управления вектором траста FT с более пологим углом наклона β приводят к более длительному времени взлета t25, но при этом, однако, одновременно обеспечивают более продвинутое курсовое перемещение экипажа sx, приводит к постановке простейшей оптимизационной задачи: рассмотреть варианты достижения определенной точки траектории движения экипажа (pz, sx) с привлечением в качестве критерия эффективности t25 , либо vx, либо суммарные энергозатраты FxzmSum.
В качестве примера, рассмотрим движение к опорной точке (pz, sx) = (25 м, 725 м) (см. вариант 4, β = 77,9° в табл. 2) под действием того же траста FT = 90 кН, но, однако, с реализацией комбинированного временнóго сценария изменения угла β: {t = 0, 5, 19, 20, 21, 40; β = 90, 90, 76, 73, 70.15, 70.15}. Несмотря на кусочно-линейный характер изменения этого задающего вектора управления FT, траектория движения экипажа – довольно гладкая (см. рис. 11).
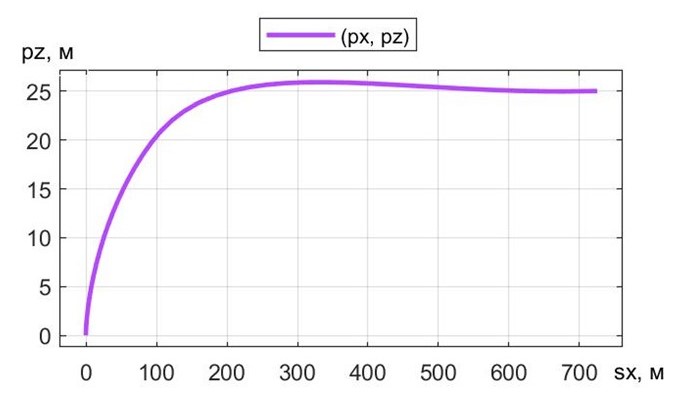
Рисунок 11 - Траектория движения ПОТ Davis к точке pz = 25 м, sx = 725 м с реализацией комбинированного сценария изменения угла β
5. Заключение
Разработанная в среде авторской Simulink-модели приземного движения квантомобиля (МПДК) Подсистема расчета энергозатрат (ПРЭ) Energetics позволяет проводить расчетное исследование энергозатрат: как на преодоление продольных сил сопротивления движению, так и на вертикальное вывешивание экипажа с обеспечением его устойчивости в плоскости тангажа.
Эта модель, по мнению автора, должна стать, во-первых, базой для оптимизационных расчетов взлета квантомобиля во многообразии его конфигураций и условий движения по ОП и рельефу местности, а во-вторых, – составной частью алгоритмов расчета динамических и траекторных показателей произвольного движения квантомобиля.
На базе проведенных посредством МПДК с ПРЭ расчетов и их анализа преодолена познавательная сложность компонентного представления энергозатрат при взлете квантомобиля в плоскости тангажа.
Проведенное исследование позволило утвердиться в гипотезе: при исследовании энергозатрат на взлет квантомобиля возможно расщепленное представление этих затрат по видам продольных и вертикальных составляющих траста и сил воздействия среды движения на экипаж – со сведением компонентных энергозатрат в их скалярную сумму.
Дальнейшие исследования должны быть направлены на рассмотрение возможности применения развиваемого подхода к оптимизации траекторий движения квантомобилей, возможно, главным образом, беспилотных. Для этого понадобится, в первую очередь, привлечение комбинирования величинами и углами траста c использованием оптимизационных методов.
