INCREASE OF ACCURACY OF POSITIONING OF MOBILE STATIONS IN CELLULAR SYSTEMS BASED ON WAVE EQUATIONS

Зотов К. Н.¹, Кузнецов И. В.², Жданов Р.Р.³, Гумерова И. И.⁴

¹Кандидат технических наук, ²Доктор технических наук, ³Кандидат технических наук, ⁴студ. спец. Инфокоммуникационные технологии и системы связи

ПОВЫШЕНИЕ ТОЧНОСТИ ПОЗИЦИОНИРОВАНИЯ МОБИЛЬНЫХ СТАНЦИЙ В СИСТЕМАХ СОТОВОЙ СВЯЗИ НА ОСНОВЕ ВОЛНОВЫХ УРАВНЕНИЙ

Аннотация

Рассматривается возможность применения волновых уравнений для повышения точности позиционирования мобильных станций в системах оператора сотовой связи, позволяющей учесть задержку распространения радиосигнала  в условиях городской застройки.

Ключевые слова: волновые уравнения; уравнения Гельмгольца; функция управления; позиционирование мобильных станций.

Zotov K. N.¹, Kuznetsov I. V.², Zhdanov R.R.³, Gumerova I. I.⁴

¹Candidate of Technical Sciences, ²Doctor of Technical Sciences, ³Candidate of Technical Sciences, ⁴student

INCREASE OF ACCURACY OF POSITIONING OF MOBILE STATIONS IN CELLULAR SYSTEMS BASED ON WAVE EQUATIONS

Abstract

The possibility observed here is about application of wave equation to increase the accuracy of positioning of mobile stations in cellular system that gives the opportunity to control delay in radio signal propagation within the urban area.

Keywords: wave equation; Helmholtz equation; control function; positioning of mobile stations.

The positioning of mobile stations is important part of mobile systems operation.[1] There are disadvantages of positioning ways of mobile stations inside the system: wave nature of radio signal propagation is not taken into consideration, delays in time, change in permittivity of environment, multipath propagation of signal, noise in radio channels [2].

It is possible to use static models of radio waves propagation [3] in the internal (ground borne) ways to increase the positioning accuracy. However the signal delay which is not considered by static models is an important factor that influences the accuracy of positioning. Thus it is supposed to apply wave equations.

Solution to Helmholtz equation is given in [4, 5] as follows:

   (1)

A₁ and A₂  –amplitudes of electromagnetic waves (picture 1), ω – frequency of a radio signal with ‘+’or ‘-‘,  τ –  spatial coordinate presented as τ(m, r) (m – direction, r – desired distance),  c – signal propagation velocity, ӄ– value that characterizes rate of decrease of wave amplitude in direction of propagation called the absorption index (should be distinguished from absorption coefficient k^//=𝟂ӄ/c), n = с/v is the value called refractive index.

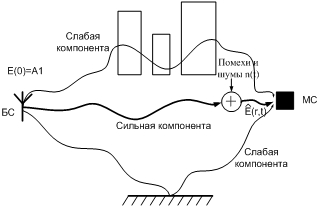Fig. 1 - Representation of the model link

 

According to the supposed model of channel (picture 1) it is necessary to consider noise in channel i.e. . Let white Gaussian additive noise n(t) with spectral density N₀ be there in channel. Mathematically contribution function of this noise will correspond to the formula:

  (2)

where . Hence the input of the receiver is fed:    (3)

Next step is to determine the distance r along the strongest component of the signal propagation. The positioning task is to find r that satisfies terms of salvation for single-beam propagation of signal [6].

The algorithm enumerates all the possible values of r along the propagation of the ray chooses:

   (4)

Figure 2 shows diagram of optimal receiver for current way.  Value of quantity r is to be selected to minimize the signal distortion.

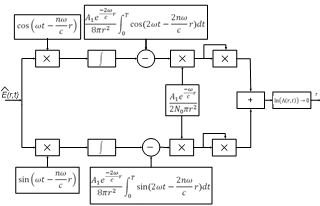
Fig. 2 - The scheme of the optimal receiver

 

The E, r obtained will be the salvation of the task.

The way described above considers criteria of propagation environment such as turbulence of environment, multi-beam rays [7], wave character of propagation in space, being a complex mathematical model in space [8].The solution of equation describing this model requires strong computing resources and understanding of complex physical processes that complicates the implementation of this way. One more advantage of current positioning way is compatibility with existing schemes of correlation detection of a signal.

References

1. A. Soshnikov, N. P. Vorob’ev, T. E. Titov “Control of electromagnetic environment at sites with sources of electromagnetic radiation” (in Russian), in Polzunovski vestnik, no. 4, pp. 64-68, 2012.
2. V. Khokhlow and S. A. Akhmanov, Problems of nonlinear optics (electromagnetic waves in nonlinear dispersive media), (in Russian). Moscow: AN SSSR, 1964.
3. N. Zotov, Efficiency cellular systems based clustering relevant location of mobile stations, (in Russian). Ufa: UGATU, 2014.
4. U. Aranovskiy, Radio system, (in Russian). Moscow: Vysshaya shkola, 1979.
5. Gra­werd, I. Lib, and V. Fisher, Differential and integral calculus, (in Russian). Moscow: Mir, 1971.
6. Sklyar, Digital communication, (in Russian). Moscow: Vil’yams, 2003.
7. N. Zotov and I. V. Kyznetsov, “The development of an algorithm to improve the positioning accuracy of mobile stations based on the calculation of the statistical parameters of the electromagnetic field in an inhomogeneous medium,” (in Russian), in Vestnik UGATU, vol. 17, no. 2 (55), pp. 14-19, 2013.
8. N. Zotov and I. V. Kyznetsov, “Improving the accuracy of positioning mobile stations based on the calculation of the statistical parameters of the electromagnetic field using Maxwell’s equations,” (in Russian), in Elektrotekhnicheskie I informatsionnye kompleksy I sistemy, vol. 9, no. 1, pp. 89-92, 2013.