MODELLING THE TRAJECTORY OF A SCOOP CHAIN IN THE BOTTOM-HOLE AREA DURING DREDGE WORK OF ALLUVIAL DEPOSITS

Дражный метод – один из основных способов разработки россыпных месторождений. 27,9% (82,84 т.) добытого в России золота в 2021 году получено многочерпаковыми драгами

Для наиболее полного извлечения запасов из месторождений, а также для оптимизации дражных работ необходимо иметь наиболее полную картину процессов, происходящих при разработке россыпных месторождений

Целью исследования является разработка модели для определения координат контура черпаковой цепи, составляющих основу формирования контура поверхности эфельных отвалов в призабойной зоне с целью определения величины разубоживания хвостами эфельных отвалов драги.

Для достижения поставленной цели были поставлены следующие задачи: построение физической модели черпаковой цепи; получение математических уравнений, описывающих координаты черпаковой цепи, при этом учитывающих такие переменные как: угол наклона черпаковой рамы и длину черпаковой цепи.

В ходе исследования была рассмотрена проблема, сопутствующая дражному способу – разубоживание песков эфельными частицами в призабойной части дражного разреза. Данная проблема возникает по причине того, что хвосты эфельных отвалов достигают призабойной части дражного разреза, что влечет за собой зачерпывание фракций, слагающих эфельный отвал, впоследствии ухудшая процесс обогащения, а также приводит к падению производительности драги

При исследовании величины разубоживания песков хвостами эфельных отвалов в зоне забоя драги наибольшую важность представляет та часть цепи, которая с большой вероятностью принимает участи в процессе выемки грунтовых частиц эфельного отвала. Данная работа направлена на определение пространственного положения контура холостого хода черпаковой цепи. Черпаковая цепь представляет собой шарнирно-соединенные между собой черпаки. Соединение между черпаками осуществляется пальцами. Для определения контура сконструирован макет черпаковой рамы с черпаковыми барабанами в соответствии с линейными размерами известных драг. За прототип была принята модель наиболее распространенной драги 250Д. Модель выполнена в масштабе 1:50. Вращение черпаковой цепи вокруг верхнего черпакового барабана (с координатами [0,0]) позволил получить графически контур холостой части цепи при любом угле наклона.

Контура черпаковой цепи получены с различными переменными, такими как угол наклона черпаковой цепи (от 15 до 45 град.), длина цепи (от 81 до 85 черпаков). Полученные координаты контура цепи, ограниченные продольной осью верхнего и нижнего черпакового барабана, точки A3 и A1 соответственно. Положение черпаковой цепи представлено на рисунке 1. Координаты точек A1 и A3 описываются следующими уравнениями:

(1)

(2)

(3)

(4)

где и – радиус нижнего черпакового барабана и верхнего черпакового барабана, соответственно, м; – длина черпаковой рамы, м; – угол наклона черпаковой рамы, град.

Координаты контура черпаковой цепи описываются следующим уравнением:

(5)

где и – эмпирические коэффициенты, которые зависят от длины черпаковой цепи и угла наклона черпаковой рамы, доли. ед.; – значения по оси абсцисс, м.

Эмпирические коэффициенты и представлены в таблицах 1–3.

Для всех условий, представленных в таблицах 1–3 и используя уравнение (5) определяем координаты экстремума дуги контура цепи (). Координаты точки представлены в таблице 4.

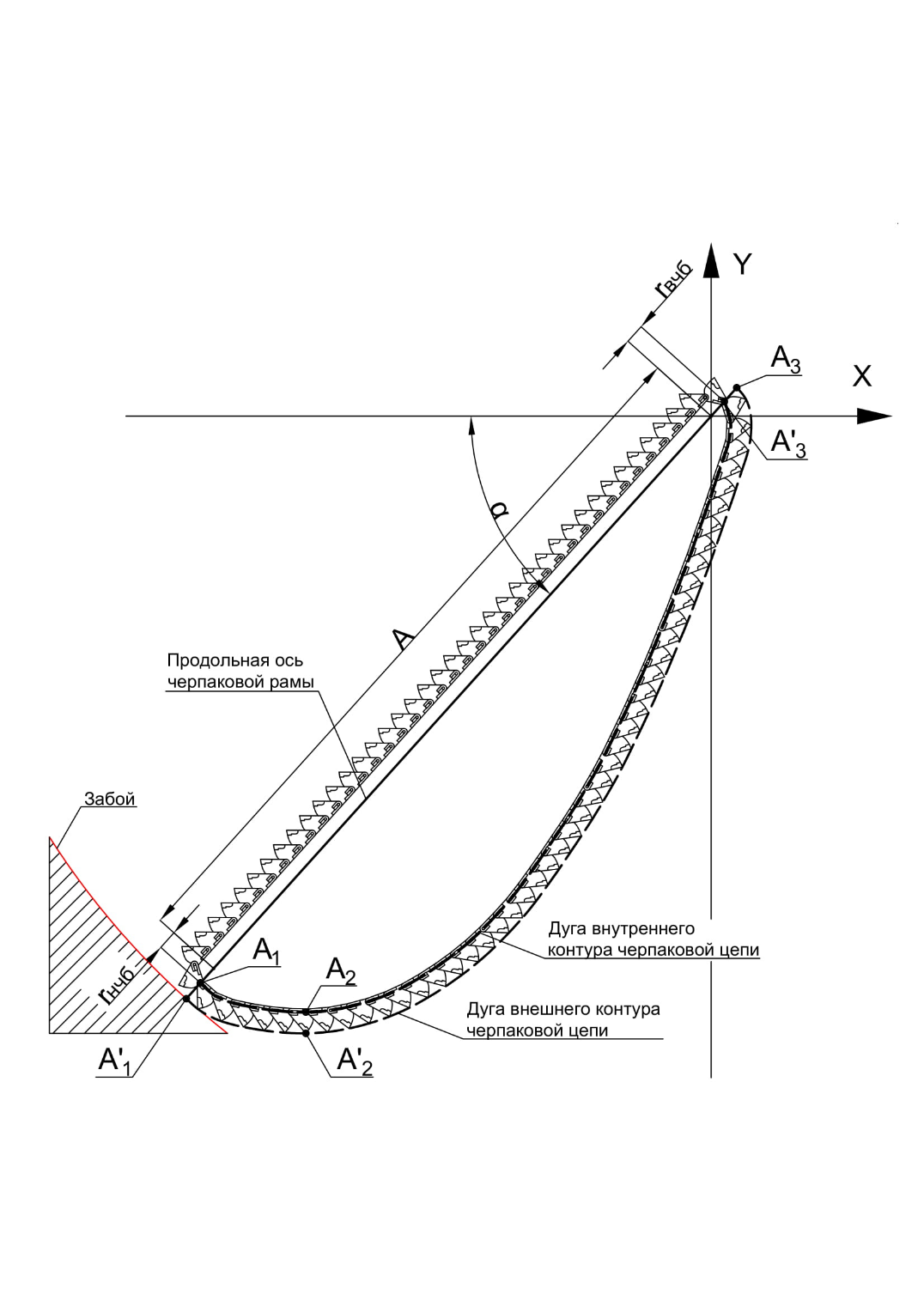
Рисунок 1 - Положение черпаковой цепи в дражном забое

DOI:10.23670/IRJ.2024.140.1.4

Вышеприведенная методика позволяет определить координаты точек внутреннего контура черпаковой цепи. Для определения координат внешнего контура, используя метод интерполяции, определим координаты точек внешнего контура. Высота черпака составляет 1057 мм, таким образом, используя уравнения 1–4, с тем учетом, что к радиусам верхнего и нижнего черпаковых барабанов необходимо прибавить высоту черпака, можно получить уравнение координат внешнего контура цепи.

Далее необходимо определить эмпирические коэффициенты для полученных уравнений координат внешнего контура и точки экстремума. Коэффициенты и координаты представлены в таблицах 5–8.

Используя полученные значения, представленные в таблицах 5–7 и 9, возможно вычислить координаты точек внешнего контура цепи. Модель учитывает длину черпаковой цепи и угол наклона цепи.

Координаты точек на дуге внешнего контура цепи определяются следующим уравнением:

(6)

где и – коэффициенты, которые зависят от длины черпаковой цепи и угла наклона черпаковой рамы.

(7)

где и – коэффициенты, которые зависят от длины черпаковой цепи по внутреннему контуру:

(8)

где – длина черпаковой цепи по внутреннему контуру, м; ,  и  – константы (табл. 9).

Пример расчета координат точек на внешнем и внутреннем контуре

Исходные данные: x=-15 м; A=31,7 м; ; n=82; ; .; м; ; ; .

Координаты точек на внутреннем контуре:

(9)

(10)

(11)

(12)

(13)

Координаты точек на внешнем контуре:

(14)

В результате данной работы разработана математическая модель расчета координат внешнего и внутреннего контуров черпаковой цепи. Данная модель учитывает такие переменные, как: угол наклона черпаковой рамы, а также длину черпаковой цепи. Модель получена для драги 250Д, но также возможно ее применение для других стандартных типоразмеров драг. Таких как 80Д, 150Д и других, так как имеют такое же отношение длины цепи к черпаковой раме. Зная координаты контура черпаковой цепи, появляется возможность для построения модели, которая может стать основой для определения объемов разубоживания хвостами эфельных отвалов в призабойной зоне дражного разреза.