OPTIMAL AUTOPILOT DESIGN ON THE BASIS OF GENETIC ALGORITHM
Нгуен М.Х.
Кандидат технических наук автоматического управления,
Вьетнамский государственный технический университет имени Ле Куй Дона, г. Ханой, Вьетнам
ПРОЕКТИРОВАНИЕ ОПТИМАЛЬНОГО АВТОПИЛОТНОГО БЛОКА НА ОСНОВЕ ГЕНЕТИЧЕСКИХ АЛГОРИТМОВ
Аннотация
Автопилотный блок играет ключевую роль в контуре управления. Сможет ли ракета входить в траекторию? Это зависит от качества автопилотного блока, поскольку он обеспечивает, чтобы ракета соблюдала упраленческие команды, полученные от навигационной системы. В данной статье предложен метод расчета коэффициентов автопилотного блока для самонаводящихся ракет на основе генетических алгоритмов, в которых критериием оценки оптимальности автопилотного блока считаются параметры качества автопилотного блока. В статье также проводится моделирование с целью сравнения и выделения оптимальности коэффициентов автопилотного блока, полученных из предложенного метода расчета коэффициентов, и из обычного метода.
Ключевые слова: автопилотный блок, генетический алгоритм, система управления полетом, автопилот.
Nguyen M.H.
Nguyen Minh Hong – PhD in Automatic Control,
Le quy don technical university, Hanoi, social republic of Vietnam
OPTIMAL AUTOPILOT DESIGN ON THE BASIS OF GENETIC ALGORITHM
Abstract
Autopilot plays a key role in the control loop. Whether or not the missile enters the trajectory depends on the quality of the autopilot because it is responsible for ensuring that the missile follows the commands received from the guiding system. A method for designing autopilot’s coefficients for homing missile on the basis of genetic algorithm, in which the criteria for evaluating the optimality of obtained autopilot are the characteristic quality parameters of the autopilot, will be proposed in this article. Simulations are conducted for the purpose of comparing and highlighting the optimality of autopilot’s coefficients obtained from the proposed design method and from the conventional design method.
Keywords: Autopilot plays, genetic algorithm, flight control system, autopilot.
Introduction
The flight control system is one element in the missile homing loop with four basic elements: autopilot, actuator, airfame dynamics and inertial measurement unit (IMU) [1], in which the autopilot is the most important element which is responsible for ensuring that the missile follows guiding commands. Therefore, the autopilot must be able to respond quickly to the mobility of the target and to ensure the stability of the system when facing impacts from random factors. Mathematically, the autopilot is a set of equations receiving guiding commands and response signals from IMU which will be calculated according to the equations to determine the control task command [1]. Typically, the design of a autopilot is a process of determining autopilot’s coefficients. In order to determine the autopilot’s coefficients, the flight control system has been analyzed in both frequency and time domains to find the constraints between the autopilot’s coefficients and the open loop cutoffs, time constants and attenuation coefficients of the flight control system in document [2], thence the set of equations has been solved to determine the autopilot’s coefficients. Therefore, the obtained quality of the autopilot is not as accurate as the original expectation. In addition, according to document [3], the guiding system must operate under frequent influences of random factors which may increase the frequency and lead to system instability.
Since it is difficult to accurately determine the quality of autopilot on the basis of cutting frequency, it is necessary to find a method to determine the autopilot’s coefficients based on its basic task which is following guiding command. A method for designing optimal autopilot’s coefficients based on genetic algorithm (GA) with the objective function is the function of two parameters that demonstrate clearly the quality of autopilot: set time and undershoot will be proposed in this article. The set time indicates the system’s rapid response, while the undershoot represents the “non-minimum phase” effect which is typical for homing missile with control task located at the tail. The non-minimum phase effect is interpreted as the response of the system at the initial stage of the reverse control process to the desired response, which not only causes some difficulties in controlling process but also reduces the system’s rapid response. As for the method for designing autopilot’s coefficients proposed in document [2], the author did not solve this problem. However, by applying the undershoot parameter to the objective function when performing GA, the autopilot’s coefficients will be optimized to reduce the influences of this effect on the controlling process.
The obtained autopilot from the proposed design method will be verified through simulations in both frequency and time domains in order to clearly identify the advantages of this method over the design method used in document [2].
Flight control system model
A three-loop autopilot for homing missile with control task located at the tail, as shown in figure 1, will be used in this article.

Fig. 1 – Homing missile with control task located at the tail
During the design process, the autopilot will be considered in connection with other elements of flight control system. Then, the input of the flight control system will be the missile normal acceleration command and the output will be the received missile normal acceleration . The diagram of flight control system with autopilot is shown in figure 2 [2, 8].
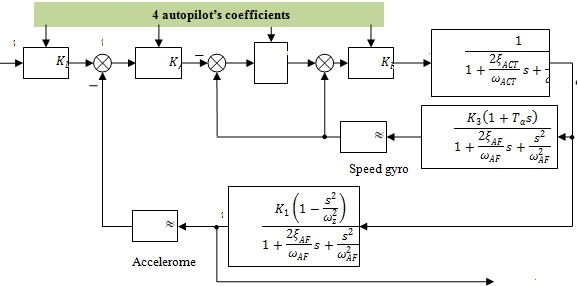
Fig. 2 – Structure diagram of the flight control system
In which:
- ![]() are four autopilot’s coefficients. The values of these coefficients depend on each method of autopilot design.
are four autopilot’s coefficients. The values of these coefficients depend on each method of autopilot design.
- ![]() and are damping coefficient and free oscillation frequency of autopilot.
and are damping coefficient and free oscillation frequency of autopilot.
- ψ is the declination of missile longitudinal axis.
- ![]() are the deviations of control tasks.
are the deviations of control tasks.
- Speed gyro and accelerometer are elements of autopilot and their dynamics are approximated 1.
- ![]() and are damping coefficient and free oscillation frequency of missile, these two parameters depend on different flight conditions according to the following expression [2]:
and are damping coefficient and free oscillation frequency of missile, these two parameters depend on different flight conditions according to the following expression [2]:
![]() (1)
(1)
- ![]() are amplification coefficients of the missile by angle channel and normal acceleration channel, they are defined as follows [2]:
are amplification coefficients of the missile by angle channel and normal acceleration channel, they are defined as follows [2]:
![]() (2)
(2)
- ωz is determined by expression (3) [2]:
![]() (3)
(3)
- Tα is determined by expression (4) [2]:
![]() (4)
(4)
In expressions (1), (2), (3) and (4), VM is missile speed, ![]() are aerodynamic coefficients depending on different flight conditions of missile.
are aerodynamic coefficients depending on different flight conditions of missile.
It can be seen from figure 2 that Raytheon autopilot has three feedback loops: speed feedback loop, stability feedback loop and normal acceleration feedback loop and the normal feedback loop. Corresponding to those three feedback loops are three autopilot’s coefficients: ![]() coefficient is responsible for ensuring that the set value of missile normal acceleration is equal to the input normal acceleration command value of flight control system, thus KDC will be calculated by
coefficient is responsible for ensuring that the set value of missile normal acceleration is equal to the input normal acceleration command value of flight control system, thus KDC will be calculated by ![]() . Then, the design of autopilot is actually the determination of three autopilot’s coefficients:
. Then, the design of autopilot is actually the determination of three autopilot’s coefficients: ![]() . In the next part of the article, the method for determining these three autopilot’s coefficients based on GA will be presented.
. In the next part of the article, the method for determining these three autopilot’s coefficients based on GA will be presented.
Optimization of autopilot by genetic algorithm
Before optimizing two autopilot’s coefficients, the closed-loop transmission function of the flight control system will be defined in this article. For this purpose, the flight control system is represented as an open loop in figure 3.
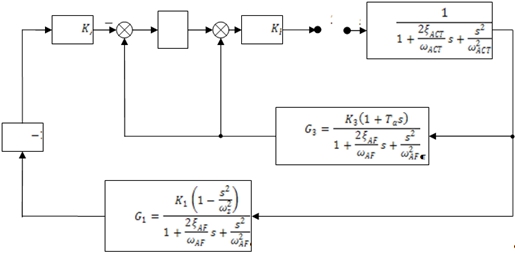
Fig. 3 – Open structure diagram of the flight control system
From figure 3, after the algebraic transformations, we have the shortened open-loop transmission function of the flight control system as follows:
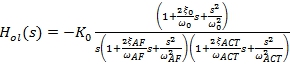 (5)
(5)
with
![]() (6)
(6)
in which KDC is determined according to [2] to ensure that the response value of the flight control system is 1. Accordingly:
![]() (8)
(8)
The idea of applying the principles of evolution in nature to the artificial intelligence system was mentioned about 4 decades ago. GA was only officially introduced by John Holland after 1970. Nowadays, GA is used to solve complex problems in various areas: optimization, automatic programming, machine learning, economics, evolution research, etc. The following advantages have contributed to the success of GA: good searching capability, capability to work in large and unknown searching space despite the lack of information; capability to work on the basis of random elements rather than rules, capability to solve problems that have many partial roots or are affected by noise; capability to simultaneously find many solutions for one problem [4]; etc.
GA has several different versions such as: binary GA, denary GA or real-coded GA. Real-coded GA will be used in this article to determine autopilot’s coefficients because it allows direct coding of parameters to be optimized, which creates the shortest chromosome length. Therefore, in general, the time to implement real-coded GA is the fastest among the three above GA versions. The implementation structure of genetic algorithm is shown below in figure 4 [5]:
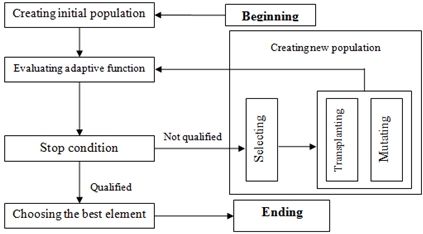
Fig. 4 – Flowchart for implementation of GA
- Creating initial population: the initial population was randomly created with a population size of N = 50, each individual in the population contains a chromosome with three genes corresponding to three autopilot’s coefficients ![]() .
.
- Adaptive function: adaptive function is the function of set time ts and lower mutation Mu. Adaptive function ![]() is as follows:
is as follows:
![]() (9)
(9)
in which k1 and k2 are the two weights that determine the role of ts and Mu during GA optimization process.
- Stop condition: GA implementation process will stop at 100 generations or after 30 generations whose adaptive function changes do not exceed 10-6.
- Genetic operations: Linear ranking selection; ![]() transplantation with transplantation probability pc= 0.8; non-identical mutation with the parameter b= 5 and mutation probability pm= 01.
transplantation with transplantation probability pc= 0.8; non-identical mutation with the parameter b= 5 and mutation probability pm= 01.
Survey results
For the purpose of comparing the proposed design method with the design method in document [2], simulations will be conducted under the same flight conditions as in [2]. Specifically, the response of the flight control system at two amplitude values of 0 m and 15240 m, ![]() will be surveyed in this article. Then, at each amplitude value, the following airfame dynamics parameters are obtained:
will be surveyed in this article. Then, at each amplitude value, the following airfame dynamics parameters are obtained:
Table 1 – Values of airfame dynamics parameters at different amplitudes
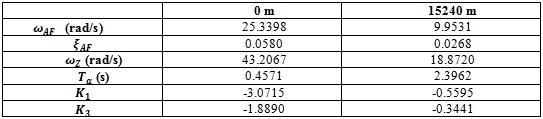
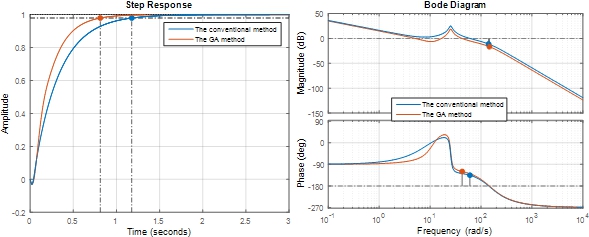 Fig. 5 – Response function of flight control system Fig. 6 – Bode diagram of flight control system
Fig. 5 – Response function of flight control system Fig. 6 – Bode diagram of flight control system
Table 2 – Values of characteristic parameters of flight control system quality at amplitude of 0 m

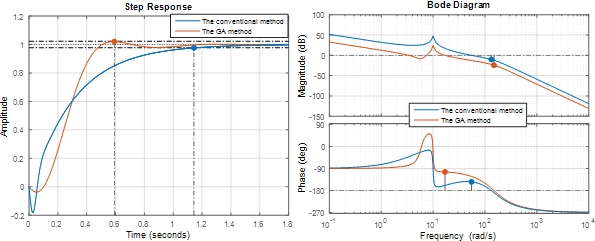 Fig. 7 – Response function of flight control system Fig. 8 – Bode diagram of flight control system
Fig. 7 – Response function of flight control system Fig. 8 – Bode diagram of flight control system
Table 3 – I Values of characteristic parameters of flight control system quality at amplitude of 15420 m

It can be observed from figure 5 and figure 7 that when the flight amplitude increases, the non-minimum phase effect increases. However, as for the autopilot obtained by the proposed method, the increase of this effect is insignificant (from 2.8% at 0 m to 3.7% at 15240 m) while as for the one obtained by conventional method, the increase of this effect is significant (from 2.9% at 0 m to 18.2% at 15240 m) [6]. Moreover, the rapid response of the autopilot obtained by GA optimization method is much better than that of the autopilot obtained by the method proposed in [2].
Although the process of designing autopilot by GA method is only performed in time domain, when surveying the autopilot obtained in frequency domain, the magnitude and phase values are all higher than those of autopilot by conventional method. This is clearly shown in figure 6, figure 8, table 2 and table 3. Furthermore, the frequency value of the flight control system by proposed method is lower than that of flight control system by conventional method. All these advantages increase the stability of the flight control system [7].
Conclusion
The proposed method for designing autopilot’s coefficients has increased the rapid response, the magnitude and phase as well as reduced the frequency of the flight control system in comparison with those of the flight control system by proposed design method in [2]. This has increased the stability of the system under influences of random factors. In addition, by incorporating the percent of overshoot parameter into the adaptive function, the influences of the non-minimum phase effect on the quality of the flight control system [8,9,10], which were not solved in document [2], have been reduced.
Список литературы / References
- Paul B. J. Overview of Missile Flight Control Systems / B. J. Paul, Johns Hopkins // APL Technical Digest. – 2010. - Vol. 29. - № 1. – P. 9-24.
- Zarchan P. Tactical and strategic missile guidance / P. Zarchan, Reston V.A. // American Institute of Aeronautics and Astronautics. - 2002. - 889 p.
- Nesline F. W. Why modern controllers can go unstable in practice / F. W. Nesline, P. Zarchan // J. Guid Control Dyn. – 1984. - № 7(4). – P. 495–500.
- Huynh T. H. Smart control system / T. H. Huynh // Vietnam National University: Ho Chi Minh City. – Publisher. - 2014. – P. 115–217.
- Nguyen D. T. Artificial Intelligence: Evolutionary programming - Data structure + Genetic algorithm = Evolutionary program / D. T. Nguyen // Education Publishing House. - 2008. – P. 46-58.
- White B.A. Missile autopilot design using quasi-LPV polynomial eigenstructure assignment / B.A. White, L. Bruyere, A. Tsourdos // IEEE Transaction on Aerospace and Electronic. – 2007. - Vol. 43. - № 4. - P. 1470–1483.
- Tsourdos A. Adaptive flight control design for nonlinear missile / A. Tsourdos, B.A.White // Control Engineering Practice. – 2005. - Vol. 13. - No. 3. - P. 373–382.
- Nichols R.A. Gain scheduling for H∞ controllers: a flight control example / R.A. Nichols, R.T. Reichert, W.J. Rugh // IEEE Transactions on Control Systems Technology. – 1993. - Vol. 1. - № 1. - P. 69–79.
- Rajabioun R. Cuckoo optimization algorithm / R. Rajabioun // Applied Soft Computing Journal. – 2011. - Vol. 11. - № 8. - P. 5508–5518.
- Siouris G.M. Missile Guidance and Control Systems / G.M. Siouris // Springer Science & Business Media. - New York. - 2004. - 684 p.
