USE OF SYNERGETIC APPROACH IN SIMULATION AND MODERNIZATION OF INFORMATION NETWORKS
Алексеев А.П.1, Абрамов Г. В. 2, Булгакова И.Н. 3
1Аспирант, 2доктор технических наук, профессор, 3кандидат экономических наук,
Воронежский Государственный Университет
ИСПОЛЬЗОВАНИЕ СИНЕРГЕТИЧЕСКОГО ПОДХОДА ПРИ МОДЕЛИРОВАНИИ И МОДЕРНИЗАЦИИ ИНФОРМАЦИОННЫХ СЕТЕЙ
Аннотация
При проектировании компьютерных сетей решают задачу выбора состава технических и программных средств при ограниченных ресурсах. При этом важно рассматривать сеть как систему из взаимодействующих друг с другом элементов, где может проявляться синергетический эффект. Основной характеристикой использования ресурсов сети является пропускная способность участка сети или всей сети. Это максимальный объем трафика, который может быть пропущен сетью, поэтому для оператора связи пропускная способность — это базовый показатель. В статье рассматривается задача нахождения максимальной пропускной способности компьютерной сети и оптимального маршрута, обеспечивающего эту пропускную способность, а также расширения этой сети при максимально эффективном использовании ее мощностей. При решении учитываются взаимосвязи между элементами сети, а в качестве параметров используются оценки типа трудность достижения цели.
Ключевые слова: компьютерные сети, максимальный поток, синергия, пропускная способность, трудность достижения цели.
Alekseev A.P.1, Abramov G.V.2, Bulgakova I.N.3
1Postgraduate student, 2PhD in Engineering, Professor, 3PhD in Economy,
Voronezh State University
USE OF SYNERGETIC APPROACH IN SIMULATION AND MODERNIZATION OF INFORMATION NETWORKS
Abstract
When designing computer networks, one solves the problem of selecting the composition of hardware and software with limited resources. It is very important to consider the network as a system of interacting elements, where a synergistic effect can be manifested. The main characteristic of using network resources is the bandwidth of the network or the entire network. This is the maximum amount of traffic that can be transmitted via the network, so for a telecom operator, the bandwidth is the basic rate. The paper considers the problem of finding the maximum throughput of a computer network and the optimal route, providing this capacity, as well as expanding this network with the most effective use of its capacities. The decision takes into account the interrelations between the elements of the network, and the estimates such as the difficulty in achieving a goal are used as parameters use.
Keywords: computer networks, maximum flow, synergy, throughput, difficulty in achieving goal.
Круг задач, решаемых с использованием компьютерных сетей, достаточно широк [1], и каждая из этих задач предъявляет свои специфичные требования к качеству обслуживания, обеспечиваемого сетью, что должно учитываться на этапе её проектирования. При проектировании информационных систем с той или иной степенью точности решают задачу выбора состава технических и программных средств при ограниченных ресурсах [2], которые должны быть использованы максимально эффективно.
Принцип максимально эффективного использования ресурсов сетей подразумевает возможность качественной и количественной адаптации, наиболее полное использование всех ресурсов и сервисов, надежность, доступность, безопасность [3]. Необходимо учитывать взаимодействие различных элементов и узлов сети между собой. Основной характеристикой использования ресурсов сетей, которая в различной форме учитывается при расчете и проектировании сетевых структур, является пропускная способность участка сети или всей сети. Пропускная способность — это интенсивность нагрузки, которая может быть пропущена участком сети или всей телекоммуникационной сетью с заданным качеством обслуживания. С точки зрения оператора связи пропускная способность сети связи — это максимальный объем трафика, который может быть пропущен сетью при условии соблюдения требований по качеству обслуживания, для него это базовый показатель, позволяющий прогнозировать доходы [3].
Пропускная способность не является пользовательской характеристикой, так как она говорит о скорости выполнения внутренних операций сети - передачи пакетов данных между узлами сети через различные коммуникационные устройства [4]. Зато она непосредственно характеризует качество выполнения основной функции сети, т.е. транспортировки сообщений, и во многом зависит от функционирования сети в целом как системы, поэтому чаще используется при анализе производительности сети, чем другие характеристики.
Пропускная способность измеряется либо в битах в секунду, либо в пакетах в секунду. Чаще всего при проектировании, настройке и оптимизации сети используются такие показатели, как средняя и максимальная пропускные способности [5].
Средняя пропускная способность вычисляется путем деления общего объема переданных данных на время их передачи, причем выбирается достаточно длительный промежуток времени - час, день или неделя.
Максимальная пропускная способность - это наибольшая мгновенная пропускная способность, зафиксированная в течение периода наблюдения [4].
Отметим, что большинство задач построения компьютерной сети связано более с техническими характеристиками вычислительно-коммутационных устройств [1], чем с эффективностью их использования для решения определенной задачи. Кроме того, зачастую стоит задача оптимального расширения уже существующей сети.
При решении задачи эффективного использования имеющихся ресурсов для модернизации сети важно учитывать возможность возникновения синергетических эффектов, так как узлы и каналы сети не являются изолированными и непосредственно влияют на функционирование друг друга.
В данной статье нами предлагается вариант решения задачи модернизации сети передачи данных с помощью численной модели, предназначенной для нахождения максимальной пропускной способности сети и оптимального маршрута, обеспечивающего эту пропускную способность, а также расширения этой сети с минимальными трудностями с учетом максимально эффективного использования возможностей сети. Поскольку любую сеть произвольной топологии можно представить в качестве ориентированного графа, то поставленная задача сводится к поиску максимального потока в сети с ее последующим расширением, и решается методами линейного программирования.
Рассмотрим задачу определения максимального потока между двумя выделенными узлами связной сети. Каждая дуга обладает пропускными способностями в обоих направлениях, которые определяют максимальный поток, проходящий по данной дуге. Ориентированная (односторонняя) дуга соответствует нулевой пропускной способности.
Задачу о максимальном потоке можно свести к задаче линейного программирования [6].
Пусть - поток из источника 1 в сток n. Обозначив поток в дуге (i, j) через xij получим следующую модель.
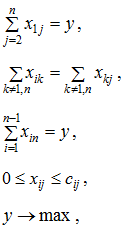
где cij пропускная способность дуги (i, j). Параметры cij сети можно представиться в матричной форме.
Алгоритм решения подобных задач подробно представлен в [6]. Решение, полученное с использованием данного алгоритма, необязательно задействует все имеющиеся пропускные способности сети, оставляя часть каналов недонасыщенными, поэтому полученный поток будем считать почти насыщенным или квазинасыщенным.
Поток можно считать максимальным тогда, когда используются все мощности сети. Для этого необходимо заполнить ненасыщенные дуги и, как следствие, расширить некоторые уже насыщенные дуги.
Для поиска ненасыщенных дуг проведём покомпонентное вычитание из матрицы пропускных способностей (исходной С) матрицу оптимального потока (X). Кроме того, приравняем нулю дуги, обратные к тем, что уже используются квазинасыщенным потоком. Таким образом получим матрицу ΔХ. На величину полученных разностей потоки по дугам должны быть увеличены для того, чтобы исходный граф обеспечивал максимальный возможный поток.
Для оценки сложности расширения различных дуг сети воспользуемся оценками трудности достижения максимального потока.
Понятие «трудность» исходит из соображений о том, что получить результат определенного качества тем труднее, чем ниже качество ресурсов, подаваемых на входе, и выше требования к качеству результат на выходе, при прочих равных условиях [7].
Если есть система, на входе которой подается набор ресурсов, необходимых для достижения результата, то величиной ![]() обозначим оценку качества ресурса i, заданную в полуинтервале
обозначим оценку качества ресурса i, заданную в полуинтервале ![]() [8]. Так как не все значения качества ресурсов достижимы, имеет смысл ввести минимальное требование к качеству ресурса
[8]. Так как не все значения качества ресурсов достижимы, имеет смысл ввести минимальное требование к качеству ресурса ![]() , так же заданное в полуинтервале
, так же заданное в полуинтервале ![]() . Невыполнение минимального требования к качеству автоматически ведет к невыполнению требований качества результата, поэтому
. Невыполнение минимального требования к качеству автоматически ведет к невыполнению требований качества результата, поэтому ![]() .
.
Для оценки качества дуги в сети возьмем отношение пропускной способности этой дуги по отношению к максимально возможной, а для оценки требования к качеству – минимальную ненулевую способность в той же сети, т.е.:
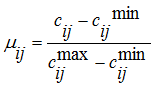 |
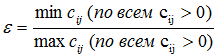 |
Формула трудности расширения дуги на единицу принимает вид [9]:
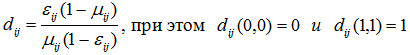
Поскольку каждая дуга в сети обладает своей трудностью расширения, логично построить матрицу трудностей D, причем ее элементы находятся по формуле [2]:
![]()
где параметр ![]() обозначает весовой коэффициент важности конкретной дуги в сети. Эти параметры находятся в диапазоне
обозначает весовой коэффициент важности конкретной дуги в сети. Эти параметры находятся в диапазоне ![]() .
.
Для определения дуг, которые необходимо расширить, воспользуемся следующим алгоритмом:
Шаг 1. Определяются весовые коэффициенты ![]() (по умолчанию 0,1) и на основе исходной матрицы С строится матрица трудностей
(по умолчанию 0,1) и на основе исходной матрицы С строится матрица трудностей ![]() .
.
Шаг 2. Выбирается ненасыщенная дуга из матрицы ![]() .
.
Можно выбирать различные исходные дуги, однако, хорошим выбором (вначале и на каждой итерации) будет минимальная безальтернативная дуга (т.е. не имеющая ненулевой обратной дуги в матрице ![]() ). Такая дуга должна быть насыщена в любом случае.
). Такая дуга должна быть насыщена в любом случае.
Значение для этой дуги из матрицы ![]() обозначим как
обозначим как ![]() .
.
Шаг 3. Определяется цепь, соединяющая s с t, и включающая в себя выбранную на предыдущем шаге дугу.
Предпочтение отдается цепи, включающей в себя другие ненасыщенные дуги, т.к. они будут насыщены при следующей итерации. Кроме того, при построении цепи необходимо избегать циклов.
Шаг 4. Насыщенные дуги, входящие в выбранную цепь, необходимо расширить на ![]() единиц, при этом трудность такого расширения оценивается как
единиц, при этом трудность такого расширения оценивается как ![]() .
.
Шаги 3-4 повторяются до тех пор, пока не будет найдена цепь с минимальной трудностью. После этого нужно перейти к шагу 5.
Шаг 5. Цепь с минимальной трудностью расширения насыщенных дуг найдена, поэтому матрица ![]() изменяется – показатель
изменяется – показатель ![]() вычитается из показателей всех дуг, задействованных в выбранной цепи, при этом показатель исходной ненасыщенной дуги становится равным нулю, а показатели насыщенных дуг становятся отрицательными (т.е. нуждаются в увеличении пропускных способностей).
вычитается из показателей всех дуг, задействованных в выбранной цепи, при этом показатель исходной ненасыщенной дуги становится равным нулю, а показатели насыщенных дуг становятся отрицательными (т.е. нуждаются в увеличении пропускных способностей).
Кроме того, если в матрице ![]() были дуги, обратные к только что насыщенным, их показатели приравниваются к нулю.
были дуги, обратные к только что насыщенным, их показатели приравниваются к нулю.
Шаг 6. Если в матрице остались положительные элементы, то нужно перейти к шагу 2. В противном случае выписывается окончательная матрица ![]() . Отрицательные элементы матрицы показывают дуги, которые необходимо расширить.
. Отрицательные элементы матрицы показывают дуги, которые необходимо расширить.
Интегральная трудность расширения находится по формуле [10]:
![]() , для всех (i,j), для которых справедливо неравенство
, для всех (i,j), для которых справедливо неравенство ![]() .
.
Исходная матрица С заменяется расширенной ![]() .
.
При этом приращение потока равно сумме всех ![]() , а максимальный поток равен сумме величины квазинасыщенного потока и этого приращения.
, а максимальный поток равен сумме величины квазинасыщенного потока и этого приращения.
Необходимо отметить, что все цепи, найденные на шаге 5, являются оптимальными решениями подзадачи поиска пути с минимальной трудностью и максимальным использованием недонасыщенных дуг. Таким образом, конечное решение, составленное из этих цепей, также будет оптимальным по данным показателям. Однако для проверки оптимальности полученного решения имеет смысл сравнить его с лучшим из вариантов, не учитывающих заполнение недонасыщенных дуг.
Если решение, учитывающее заполнение недонасыщенных дуг, дает лучший эффект, чем варианты, его не учитывающие, то есть смысл говорить о синергетическом эффекте, проявляющимся во взаимном влиянии недонасыщенных дуг сети друг на друга.
Рассмотрим предложенный подход на примере. Исходная сеть, с заданными пропускными способностями имеет вид (рис. 1).
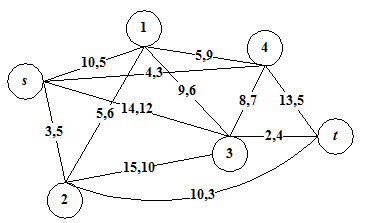
Рис. 1 – Исходная сеть, с заданными пропускными способностями
Соответствующая матрица пропускных способностей имеет вид:
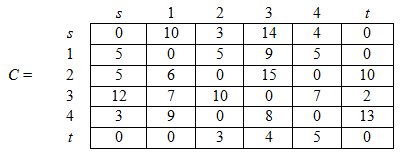
Применив алгоритм [6], получим квазинасыщенный поток (рис. 2).
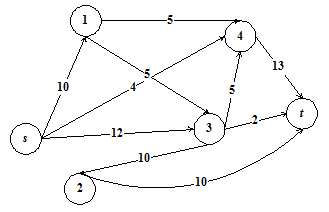
Рис 2 – Квазинасыщенный поток
Матрица полученного потока:
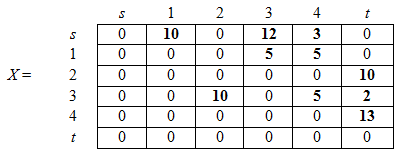
Из матрицы видно, что ![]() , это и есть величина квазинасыщенного потока.
, это и есть величина квазинасыщенного потока.
Матрица ненасыщенных дуг выглядит следующим образом:
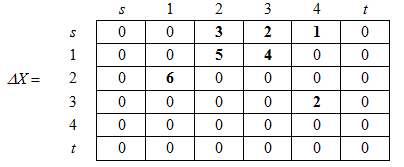
Примем все весовые коэффициенты равными 0,1:
![]()
Матрица трудностей с учетом этих коэффициентов имеет вид:
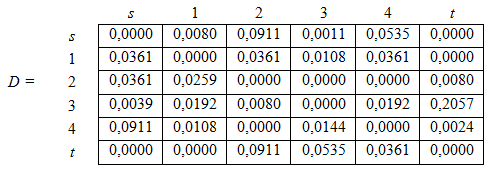
В качестве первой дуги выбираем ![]() ,
,
Единственная цепь, включающая эту дугу, это ![]() , поэтому мы можем пометить дугу
, поэтому мы можем пометить дугу ![]() на расширение и изменить матрицу, вычтя 1 из ячеек (s,4) и (4,t).
на расширение и изменить матрицу, вычтя 1 из ячеек (s,4) и (4,t).
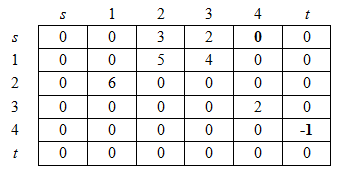
В качестве следующей дуги можно принять ![]() .
Эта дуга входит в несколько цепей, а именно
.
Эта дуга входит в несколько цепей, а именно ![]() и
и ![]() .
.
Заметим, что дуга ![]() тоже недонасыщена на 2 единицы. Поскольку обратная дуга (
тоже недонасыщена на 2 единицы. Поскольку обратная дуга (![]() ) отсутствует в матрице, мы в любом случае попытаемся насытить эту дугу в одной из следующих итераций, поэтому можно сразу выбирать цепь
) отсутствует в матрице, мы в любом случае попытаемся насытить эту дугу в одной из следующих итераций, поэтому можно сразу выбирать цепь ![]() .
.
Вычитаем число 2 из ячеек (s,3), (3,4) и (4,t).
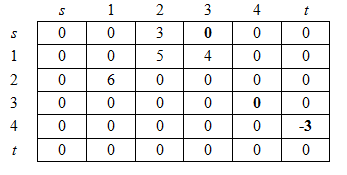
Следующая минимальная дуга это ![]() . Она входит в цепь
. Она входит в цепь ![]() и несколько цепей
и несколько цепей ![]()
Заметим, что поскольку дуги ![]() также ненасыщенные, то создается впечатление, что оптимальный путь пролегает через эти них, однако существует обратная дуга
также ненасыщенные, то создается впечатление, что оптимальный путь пролегает через эти них, однако существует обратная дуга ![]() , поэтому насыщение
, поэтому насыщение ![]() не является безальтернативным.
не является безальтернативным.
Интегральная трудность цепи ![]() меньше, чем у цепей
меньше, чем у цепей ![]() (0,0159 против 0,205 и 0,0215 соответственно), но она содержит цикл
(0,0159 против 0,205 и 0,0215 соответственно), но она содержит цикл ![]() , что недопустимо. Цепь
, что недопустимо. Цепь ![]() имеет еще меньшую трудность 0,008, поэтому именно ее следует выбрать в качестве оптимальной.
имеет еще меньшую трудность 0,008, поэтому именно ее следует выбрать в качестве оптимальной.
Матрица принимает вид:
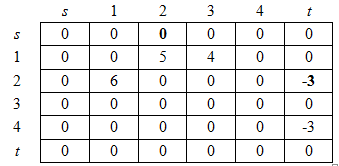
Предыдущая итерация показала, что цепи, включающие дугу ![]() , имеют большую трудность насыщения, чем цепи с дугой
, имеют большую трудность насыщения, чем цепи с дугой ![]() . Поэтому следующей выберем дугу
. Поэтому следующей выберем дугу ![]() , при этом обратная дуга станет равна нулю.
, при этом обратная дуга станет равна нулю.
Она входит только в одну цепь ![]() , поэтому матрица изменяется соответственно:
, поэтому матрица изменяется соответственно:
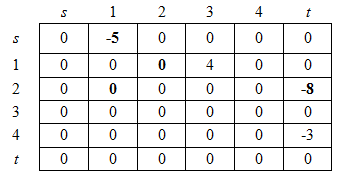
Осталась только дуга ![]() . Поскольку мы уже вычислили, что цепь
. Поскольку мы уже вычислили, что цепь ![]() лучше альтернатив, проходящих через узлы 3 и 4, то оптимальной становится цепь
лучше альтернатив, проходящих через узлы 3 и 4, то оптимальной становится цепь ![]() .
.
После преобразования получаем конечную матрицу ![]() :
:
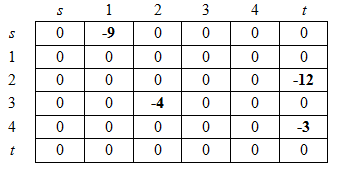
Интегральная трудность насыщения сети равна:
![]()
Графическое решение представлено на рисунке 3:
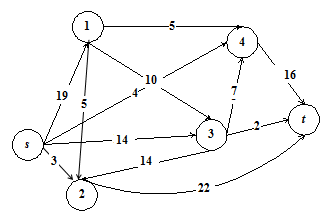
Рис. 3 – Графические решение
Вычислим новую матрицу С*:
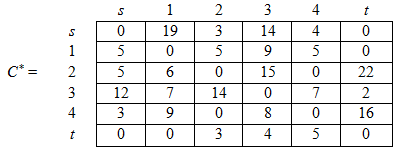
Наконец, найдем приращение квазинасыщенного потока:
![]()
Для проверки оптимальности найдем лучшее решение задачи расширения без оглядки на ненасыщенные дуги. Для этого необходимо найти цепь с минимальной трудностью расширения и увеличить все ее каналы так, чтобы по этой цепи могло пройти приращение потока ![]() .
.
В нашем примере это цепь ![]() , дуги
, дуги ![]() и необходимо расширить на 15, дугу
и необходимо расширить на 15, дугу ![]() - на 13 (т.к. она недонасыщена на 2). Интегральная трудность насыщения будет равна:
- на 13 (т.к. она недонасыщена на 2). Интегральная трудность насыщения будет равна:
![]()
Сравнив этот результат с полученным ранее, можно сделать вывод, что найденное нами решение является наименее трудоемким вариантом расширения сети с использованием всех недонасыщенных каналов.
Таким образом, полученная нами модель отражает синергетический подход к решению задачи модернизации информационной сети с целью увеличения ее пропускной способности. Учет недонасыщенных каналов связи и их влияния друг на друга позволяет найти более оптимальный вариант расширения, нежели простое увеличение наиболее удобных для этого потоков.
Представление квазинасыщенной сети в виде системы взаимосвязанных элементов позволяет говорить о получении синергетического эффекта, который обеспечивает максимальный достижимый при ограниченных ресурсах поток наименее трудоемким способом.
Список литературы / References
- Катаев М.Ю., Крупский А.С. Оценка пропускной способности на основе модели однородной сети / М.Ю. Катаев, А.С. Крупский // Доклады ТУСУРа. - № 2 (36). - июнь 2015.
- Таненбаум Э. Компьютерные сети / Э. Таненбаум . – СПб.: Питер, 2008. – 992 с.
- Степанова И. В., Булатов С. В. Методы повышения пропускной способности уровня абонентского доступа / И. В. Степанова, С. В. Булатов // Журнал T-Comm - Телекоммуникации и Транспорт. - № 2 - 2009.
- Куделькина Н.Н. Системы передачи данных. Курс лекций для специальности 210407 «Эксплуатация средств связи» / Н.Н. Куделькина. Томский техникум железнодорожного транспорта. – Томск. - 2010.
- Втюрин В.А. Автоматизированные системы управления технологическими процессами. Основы АСУТП: Учебное пособие для студентов специальности 220301 "Автоматизация технологических процессов и производств" / В.А. Втюрин. - СПб: СПбГЛТА. - 2006.
- Таха Х.А. Введение в исследование операций. 6-е издание / Х.А. Таха. : Пер. с англ. – М. : Издательский дом «Вильямс», - 2001.
- Булгакова И.Н., Саликов Ю.А. Совершенствование модели развития социально-экономических систем / И.Н. Булгакова, Ю.А. Саликов // Современная экономика: проблемы и решения. – Воронеж, - 2010 - №2(2) – С. 146-154.
- Алексеев А.П. Использование модели Р. Стоуна для оценки синергетического эффекта процесса интеграции предприятий / А.П. Алексеев // Наука и образование в жизни современного общества. - 2014. - №11. - С. 10-11.
- Руссман И.Б. Интегральные оценки качества в организационных системах / И.Б. Руссман // Сборник "Структурная адаптация сложных систем управления", - Изд. ВПИ, Воронеж. – 1977. - с. 90-92.
- Алексеев А.П. Использование трудности достижения цели для оценки синергетического эффекта при создании интегрированных структур / А.П. Алексеев, Г.В. Абрамов, И.Н. Булгакова // Международный научно-исследовательский журнал. - 2015. - №10-2 (41). - С.6-10.
Список литературы на английском языке / References in English
- Kataev M.J., Krupskij A.S. Ocenka propusknoj sposobnosti na osnove modeli odnorodnoj seti [The estimation of network capacity based on the model of homogenous network] / M.J. Kataev, A.S. Krupskij // Doklady TUSURa [Reports of TUSUR]. - № 2 (36). - June 2015. [In Russian]
- Tanenbaum A. Computer Networks / A. Tanenbaum. - Prentice Hall, 2002.
- Stepanova I. V., Bulatov S. V. Metody povyshenija propusknoj sposobnosti urovnja abonentskogo dostupa [Methods for increasing of network capacity on the level of local loop] / I. V. Stepanova, S. V. Bulatov // Zhurnal T-Comm - Telekommunikacii i Transport [Journal T-Comm – Telecommunications and transport]. - № 2. - 2009. [In Russian]
- Kudel'kina N.N. Sistemy peredachi dannyh. Kurs lekcij dlja special'nosti 210407 «Jekspluatacija sredstv svjazi» [The systems of data transfer. Lectures for specialization 210407 “Exploitation of communications facilities”] / N.N. Kudel'kina // Tomskij tehnikum zheleznodorozhnogo transporta. – Tomsk. - 2010. [In Russian]
- Vtjurin V.A. Avtomatizirovannye sistemy upravlenija tehnologicheskimi processami. Osnovy ASUTP: Uchebnoe posobie dlja studentov special'nosti 220301 "Avtomatizacija tehnologicheskih processov i proizvodstv" [Automatic control systems for technological process. Basics of ACSTP: Textbook for students of specialization 220301 “Automatization of technical processes and manufactures”] / V.A. Vtjurin. - SPb: SPbGLTA. - 2006. [In Russian]
- Taha H. A. Operations research: an introduction / H. A. Taha. - Prentice Hall, 1996.
- Bulgakova I.N., Salikov J.A. Sovershenstvovanie modeli razvitija social'no-jekonomicheskih sistem [Improving of the model of evolution of social-economic systems] / I.N. Bulgakova, J.A. Salikov // Sovremennaja jekonomika: problemy i reshenija [Modern economics: Problems and solutions]. – Voronezh, 2010. - №2 (2). – P. 146-154. [In Russian]
- Alekseev A.P. Ispol'zovanie modeli R. Stouna dlja ocenki sinergeticheskogo jeffekta processa integracii predprijatij [The using of model of R. Stone for evaluation of synergistic effect of companies integration process] / A.P. Alekseev // Nauka i obrazovanie v zhizni sovremennogo obshhestva [Science and education in life of modern society]. - 2014. - №11. - P. 10-11. [In Russian]
- Russman I.B. Integral'nye ocenki kachestva v organizacionnyh sistemah [Structure adaptation of complex control systems] / I.B. Russman // Sbornik "Strukturnaja adaptacija slozhnyh sistem upravlenija" [Collection “Structural adaptation of complex control systems”]. - Izd. VPI, Voronezh, - 1977, - P. 90-92. [In Russian]
- Alekseev A.P. Ispol'zovanie trudnosti dostizhenija celi dlja ocenki sinergeticheskogo jeffekta pri sozdanii integrirovannyh struktur [Using of the difficulty of achieving the goal for evaluation of synergetic effect in the creation of integrated structures] / A.P. Alekseev, G.V. Abramov, I.N. Bulgakova // Mezhdunarodnyj nauchno-issledovatel'skij zhurnal [International Research Journal]. - 2015. - №10-2 (41). - P. 6-10. [In Russian]
