EFFICIENCY OF BLOCK DESIGNS IN FUNCTIONAL MAGNETIC RESONANCE IMAGING
Машарипов Р.С.1, Киреев М.В.2, Коротков А.Д.3, Медведев С.В.4
1ORCID: 0000-0003-4162-3725, аспирант, 2ORCID: 0000-0003-3409-6293, кандидат биологических наук, 3ORCID: 0000-0003-3527-7205, кандидат биологических наук, 4ORCID: 0000-0003-2503-9131, академик Российской академии наук, доктор биологических наук,
Институт мозга человека имени Н.П. Бехтеревой Российской академии наук
ЭФФЕКТИВНОСТЬ БЛОКОВЫХ ДИЗАЙНОВ В ФУНКЦИОНАЛЬНЫХ МАГНИТНО-РЕЗОНАНСНЫХ ТОМОГРАФИЧЕСКИХ ИССЛЕДОВАНИЯХ
Аннотация
Настоящая работа посвящена оценке эффективности блокового дизайна функционального магнитно-резонансного томографического (фМРТ) исследования в зависимости от длительности блоков, в которых испытуемый находится в состоянии оперативного покоя. Показано, что длительность блоков «покоя» равная длительности блоков экспериментальных условий при наличии нескольких условий и/или относительной большой длительности блоков «условий» снижает эффективность блокового дизайна в обнаружении различий, связанных с повышением нейрональной активности в экспериментальных условиях по сравнению с состоянием оперативного покоя. Расчет оптимальной длительности блока «покоя» не только помогает повысить эффективность блокового дизайна, но и позволяет сократить общую длительность фМРТ-исследования, что особенно важно для диагностических исследований.
Ключевые слова: эффективность дизайна, блоковый дизайн, функциональная магнитно-резонансная томография.
Masharipov R.S.1, Kireev M.V.2, Korotkov A.D.3, Medvedev S.V.4
1ORCID: 0000-0003-4162-3725, Postgraduate student, 2ORCID: 0000-0003-3409-6293, PhD in Biology, 3ORCID: 0000-0003-3527-7205, PhD in Biology, 4ORCID: 0000-0003-2503-9131, Dr.Sci. in Biology,
N.P. Bechtereva Institute of the Human Brain.
EFFICIENCY OF BLOCK DESIGNS IN FUNCTIONAL MAGNETIC RESONANCE IMAGING
Abstract
In this paper we estimate the efficiency of block designs in functional magnetic resonance imaging (fMRI) depending on the duration of the rest blocks. It is shown that the equality of rest block and task block duration can reduces the efficiency of block design in detecting difference of neural activity between rest and task conditions. Estimation of the optimal rest block duration not only allows to improve the efficiency of block design, but also reduces the overall duration of fMRI study, which is especially important for clinical studies.
Keywords: design efficiency, block design, functional magnetic resonance imaging.
Блоковые дизайны широко применяются при функциональных магнитно-резонансных томографических (фМРТ) исследованиях. Применение блокового дизайна предполагает предъявление испытуемому однотипных стимулов с минимальным промежутком или выполнение испытуемым определенной деятельности в течение определенного интервала времени (обычно от 15 до 50 секунд) [1]. В структурах мозга, нейрональная активность которых связана с определенным экспериментальным условием, МР-сигнал, зависящий от уровня оксигенации крови (BOLD-сигнал), повышается и выходит на плато до окончания блока экспериментального условия (далее – блока «условия»). Зачастую в фМРТ-исследованиях требуется определить повышение нейрональной активности в экспериментальном условии по сравнению с состоянием оперативного покоя. Для этого блоки с «условиями» разделяют паузами, во время которых испытуемый находится в состоянии оперативного покоя (далее данные промежутки времени будут называться блоками «покоя»).
Важным аспектом создания блоковых фМРТ-дизайнов для психофизиологических исследований является минимизация общей длительности исследования, т.к. испытуемые не могут долго находится в магнитно-резонансном томографе из-за громкого звука, вызываемого механической вибрацией градиентных катушек МР-томографа (чем выше скорость регистрации данных, тем громче звук) [2], [3], из-за стимуляции периферических нервов быстрым изменением магнитного поля, приводящей к непроизвольному сокращению мышц, из-за стресса от нахождения в непривычном замкнутом пространстве, из-за затекания головы и шеи при их длительной фиксации и других факторов [4], [5]. Особую важность эта проблема приобретает при диагностических исследованиях, например, при определении речевых или моторных областей перед проведением нейрохирургической операции, т.к. пациенты еще более чувствительны к условиям сканирования в МР-томографе [6], [7].
Однако, при сокращении общей длительности исследования уменьшение количества регистрируемых данных приводит к снижению отношения сигнал-шум и, соответственно, к снижению вероятности обнаружения различий, связанных с экспериментальными условиями при статистическом анализе данных. Иными словами, снижается эффективность данного фМРТ-дизайна. В литературе уже рассматривался вопрос о зависимости эффективности блоковых дизайнов от длительности блоков «условия» (оптимальная длительность 15 с, максимальная до 50 с) [8], от порядка предъявления блоков, от периода между началом двух проб в блоке (Stimulus-onset asynchrony, SOA – чем меньше, тем лучше) [9] и других параметров. Согласно стандартной рекомендации, встречаемой в литературе посвященной эффективности блоковых дизайнов, длительность блока «покоя» должна равняться длительности блока «условия» [8]. Но на практике встречаются ситуации, когда длительность блока «условия» невозможно сократить до оптимальных 15 секунд, а также необходимо сравнение более двух экспериментальных условий. В таком случае блоки «покоя» значительно увеличивают общую длительность исследования и возникает вопрос о возможности сокращения длительности блоков «покоя» при минимальной потери эффективности дизайна. Настоящая работа была посвящена оценке эффективности блоковых дизайнов в зависимости от длительности блоков «покоя».
Для статистического анализа локальной нейрональной активности возможно использование общих линейных моделей (ОЛМ) вида [10]:
![]() (1)
(1)
Согласно ОЛМ регистрируемый сигнал Yk(t) в каждом вокселе k зависит от нескольких факторов Xkn(t), например, от экспериментальных условий, индивидуальных особенностей испытуемого, движений головы во время сканирования и др., а оставшаяся часть сигнала Ek(t) считается необъяснимой случайной ошибкой. В рамках ОЛМ предполагается, что случайная ошибка Ek(t) имеет нормальное распределение со средним значением равным нулю и выборочной (обозначено *) дисперсией σk2* (![]() ), а также предполагается, что случайная ошибка в одном вокселе не зависит от ошибки в другом вокселе. Величина параметров βn указывает на вклад того или иного фактора Xkn(t) в регистрируемый сигнал. Расчет данных параметров происходит при помощи метода наименьших квадратов, чтобы оставшаяся необъяснимая часть сигнала Ek(t) принимала минимальные значения. Таким образом, каждому вокселю фМРТ-изображения будет соответствовать свой набор параметров βn, максимально объясняющих сигнал в этом вокселе: для всего объема головного мозга строятся статистические параметрические карты (анг. «Statistical Parametric Mapping», SPM) [10].
), а также предполагается, что случайная ошибка в одном вокселе не зависит от ошибки в другом вокселе. Величина параметров βn указывает на вклад того или иного фактора Xkn(t) в регистрируемый сигнал. Расчет данных параметров происходит при помощи метода наименьших квадратов, чтобы оставшаяся необъяснимая часть сигнала Ek(t) принимала минимальные значения. Таким образом, каждому вокселю фМРТ-изображения будет соответствовать свой набор параметров βn, максимально объясняющих сигнал в этом вокселе: для всего объема головного мозга строятся статистические параметрические карты (анг. «Statistical Parametric Mapping», SPM) [10].
Систему всех ОЛМ для одного воксела, можно представить в матричном виде:
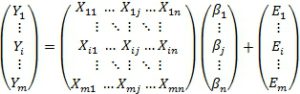 (2)
(2)
![]() (3)
(3)
Вектор-столбец Ymx1 содержит значения BOLD-сигнала в динамических сканах от 1 до m, вектор-столбец Emx1 содержит значения случайной ошибки в сканах от 1 до m (![]() ) вектор-столбец βnx1 cодержит значения параметров, определяющих вклад регрессоров от 1 до n в регистрируемый сигнал. Матрица Хmxn содержит значения всех n регрессоров для всех m сканов, её также называют матрицей дизайна исследования. Регрессоры, связанные с экспериментальными условиями, свертывают с функцией гемодинамического ответа для того, чтобы смоделировать ожидаемый BOLD-сигнал. Кроме этого к правой и левой части уравнения применятся фильтр высоких частот (ФВЧ) для того, чтобы устранить низкочастотные колебания сигнала, связанные с дрифтом магнитного поля и другими низкочастотными шумами МР-томографа. В качестве примера рассмотрим блоковый дизайн с 4 условиями, предъявляемых последовательно («условие1, «покой», «условие2», «покой», «условие3», «покой», «условие4», «покой» и т.д.), длительностью блока «условия» 20 с и длительностью блока «покоя» 20 с, а также используем стандартный для фМРТ-исследований ФВЧ [8], отсеивающий колебания с периодом более 128 с. В данном случае матрица Х будет состоять из 4 регрессоров, моделирующих амплитуду сигналов, связанных с 4 экспериментальными условиями (см. рис. 1А).
) вектор-столбец βnx1 cодержит значения параметров, определяющих вклад регрессоров от 1 до n в регистрируемый сигнал. Матрица Хmxn содержит значения всех n регрессоров для всех m сканов, её также называют матрицей дизайна исследования. Регрессоры, связанные с экспериментальными условиями, свертывают с функцией гемодинамического ответа для того, чтобы смоделировать ожидаемый BOLD-сигнал. Кроме этого к правой и левой части уравнения применятся фильтр высоких частот (ФВЧ) для того, чтобы устранить низкочастотные колебания сигнала, связанные с дрифтом магнитного поля и другими низкочастотными шумами МР-томографа. В качестве примера рассмотрим блоковый дизайн с 4 условиями, предъявляемых последовательно («условие1, «покой», «условие2», «покой», «условие3», «покой», «условие4», «покой» и т.д.), длительностью блока «условия» 20 с и длительностью блока «покоя» 20 с, а также используем стандартный для фМРТ-исследований ФВЧ [8], отсеивающий колебания с периодом более 128 с. В данном случае матрица Х будет состоять из 4 регрессоров, моделирующих амплитуду сигналов, связанных с 4 экспериментальными условиями (см. рис. 1А).
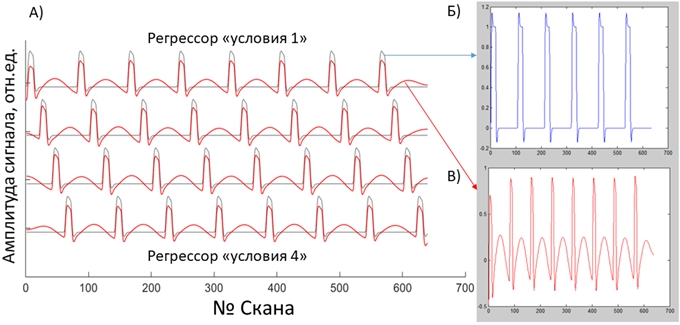
Рис. 1 – А) Относительные значения регрессоров 4 условий, определяемые матрицей дизайна Х. Б) Модель сигнала, связанного с «условием 1» до применения ФВЧ и В) после применения ФВЧ с порогом 128 с
Оценка параметров β и их выборочной дисперсии в рамках метода наименьших квадратов происходит при помощи решении систем уравнений:
![]() (4)
(4)
![]() (5)
(5)
Для определения различий, связанных с повышением сигнала в «условии1» по сравнению с покоем (т.н. контраст «условие1>покой» рассчитывается значение t-критерия Стьюдента для параметра, описывающего «условие1»:
![]() (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
где С – вектор-строка, определяющий контраст сравнения, в рассматриваемом случае для определения различия «условие1>покой» используется вектор C = [1 0 0 0], а, например, для определения различия «условие1>условие2» используется вектор С = [1 -1 0 0] и т.д.).
Согласно нулевой гипотезе H0: ![]() . Если значение t-критерия превышает критическое значение, при котором вероятность его обнаружения становится меньше выбранного исследователем порога (например, p<0.05), то различие, связанное с контрастом С
. Если значение t-критерия превышает критическое значение, при котором вероятность его обнаружения становится меньше выбранного исследователем порога (например, p<0.05), то различие, связанное с контрастом С![]() , считается статистически значимым. Для того, чтобы t-критерий достиг превысил критическое значение необходимо увеличение разности параметров С
, считается статистически значимым. Для того, чтобы t-критерий достиг превысил критическое значение необходимо увеличение разности параметров С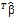 , стоящей в числителе уравнения (8), а также уменьшение числителя
, стоящей в числителе уравнения (8), а также уменьшение числителя ![]() . Как уже говорилось ранее, σ2* – это выборочная дисперсия связная с необъяснимой частью сигнала (неизвестным «шумом»). Повлиять напрямую на значение σ2* исследователь повлиять не может, однако он напрямую влияет на произведение
. Как уже говорилось ранее, σ2* – это выборочная дисперсия связная с необъяснимой частью сигнала (неизвестным «шумом»). Повлиять напрямую на значение σ2* исследователь повлиять не может, однако он напрямую влияет на произведение ![]() , называемое «дисперсией дизайна», изменяя дизайн исследования, т.к. это произведение зависит от выбранного контраста С и матрицы дизайна исследования X. Минимизируя дисперсию, связанную с дизайном, исследователь повышает эффективность дизайна в обнаружении различия, определяемого контрастом С:
, называемое «дисперсией дизайна», изменяя дизайн исследования, т.к. это произведение зависит от выбранного контраста С и матрицы дизайна исследования X. Минимизируя дисперсию, связанную с дизайном, исследователь повышает эффективность дизайна в обнаружении различия, определяемого контрастом С:
![]() (9)
(9)
Эффективность дизайна определяет способность точной оценки параметров β при заданной матрице дизайна Х. Она не имеет размерности, т.е. является относительной величиной. Если значение эффективности одного дизайна в два раза больше, чем у другого, то нельзя сказать, что этот дизайн в два раза эффективнее другого, можно только сказать, что он эффективнее.
Применение ФВС к рассматриваемому блоковому дизайну приводит к искажению моделей сигналов, связанных с условиями (см. рис. 1Б и рис. 1В), что в свою очередь приводит к увеличению «дисперсии дизайна» и снижению эффективности дизайна. Это происходит потому, что дизайн включает в себя 4 экспериментальных условия при относительно большой длительности блоков «условия» (durусл) и блоков «покоя» (durпокоя) – изменения сигнала, связанного с условиями, происходит медленно с периодом: ![]() = (20+20)×4 = 160 секунд. Часть полезного сигнала отсеивается стандартным фильтром высоких частот (см. рис. 2), который убирает низкочастотные колебания с периодом более 128 секунд (частотой ~ 0.0078 Гц).
= (20+20)×4 = 160 секунд. Часть полезного сигнала отсеивается стандартным фильтром высоких частот (см. рис. 2), который убирает низкочастотные колебания с периодом более 128 секунд (частотой ~ 0.0078 Гц).
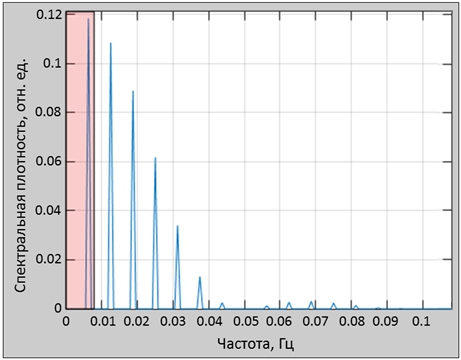
Рис. 2 – График спектральной плотности модели сигнала, связанного с «условием1», полученный при помощи быстрого преобразования Фурье. ФВЧ с порогом 128 с (~ 0.0078 Гц) отсеивает часть полезного сигнала (обозначен розовым цветом)
Расчет эффективности дизайна в зависимости от длительности блока «покоя» для контраста «условие1>покой» до применения ФВЧ показал ожидаемое увеличение эффективности при увеличении длительности блока «покоя». После применения ФВЧ с порогом 128 с эффективность дизайна увеличивается до определенной длины блока «покоя», а затем падает из-за того, что фильтр начинает отсеивать полезный сигнал (см. рис. 3). Оптимальная длительность блока «покоя» для рассматриваемого дизайна равна 11 секунд.
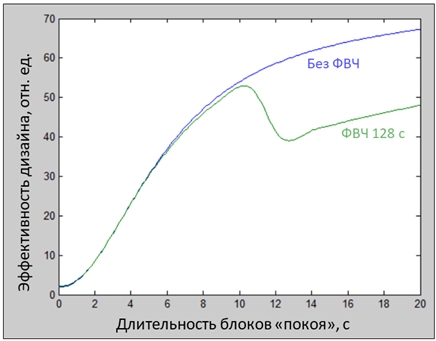
Рис.3 – Зависимость эффективности дизайна для контраста «условие1>покой» от длительности блоков «покоя». Синим – эффективность дизайна до применения ФВЧ. Зеленым – после ФВЧ с порогом 128 с
Эффективность блокового дизайна после применения ФВЧ при длительности блока «покоя» 20 с равна 48.01, а при длительности блока 11 с равна 50.47. При этом общая длительность продолжительность исследования сокращается на 22,5%. Таким образом длительность блока «покоя» равная длительности блока «условия» не является оптимальной при наличии более двух экспериментальных условий и относительно большое длительности блоков «условия». Расчет оптимальной длительности блока «покоя» позволяет дубится максимальной эффективности дизайна, сокращая при этом общую длительность исследования, что особенно важно для пациентов, испытывающих стресс от длительного нахождения в МР-томографе.
Дополняя вышесказанное необходимо отметить следующее:
1) Для блокового дизайна с последовательным предъявлением блоков «условий» (без рандомизации или контрбалансировки) оптимальную длительность блока «покоя» можно получить не только с помощью расчета зависимости эффективности блока, но и с помощью неравенства:
![]() (10)
(10)
2) Для дизайнов с длительностью блоков «покоя» равными длительности блоков «условия» при последовательном предъявлении блоков и при использовании стандартного ФВЧ 128с максимальная длительность блоков при которой не происходит снижение эффективности составляет: для 1 условия – 63 с, 2 условий – 31 с, 3 условий – 21 с, 4 условий – 15 с.
3) В случае, если блоки идут в непоследовательном порядке (с применением рандомизации или контрбалансировки порядка предъявления блоко), или при варьировании длительности блоков использование неравенства (10) становится не возможным.
4) Также использование неравенства (10) не позволяет определить оптимальную длительность блока «покоя», при такой длительности блока «условия», при которой любое изменение длительности блока «покоя» не позволит сократить период колебания полезного сигнала ниже порога 128 с, который отсекает стандартный фильтр ФВЧ. Для 2 условий – это происходит при приближении длительности блока к 63 с, для 3 условий при 42 с, для 4 условий при 31 с.
5) В ситуации (3) и (4) определение оптимальной длительности блока «покоя» возможно при помощи уравнения (9) и построения графика зависимости эффективности от длительности блока «покоя» (рис. 3).
6) Альтернативный способ повышения эффективности дизайна в ситуациях (3) и (4) – применение менее строго порога ФВС, чем общепринятый [8] порог 128 с. Однако, для этого необходимо знать какие низкочастотные шумы возникают у конкретного МР-томографа, на котором будут регистрируются данные. Перед использованием менее строго порога исследователь должен убедиться, отсеивает ли такой фильтр низкочастотные шумы МР-томографа.
Список литературы / References
- Petersen S.E. The mixed block/event-related design / S.E. Petersen, J.W. Dubis // Neuroimage. –2012. – Vol.62, №2. – P. 1177–1184.
- Moelker A., Pattynama P.M. Acoustic noise concerns in functional magnetic resonance imaging / A. Moelker, P.M. Pattynama // Human Brain Mapping. – 2003. – Vol.20, №3. – P. 123–141.
- McJury M., Shellock F.G. Auditory noise associated with MR procedures: A Review / M. McJury, F.G. Shellock // Journal of Magnetic Resonance Imaging. – 2000. – Vol.12. – P. 37–45.
- Cooke R. The neuroimaging research process from the participants' perspective / R. Cooke [et al.] // International Journal of Psychophysiology. – 2007. Vol.63. – P. 152–158.
- MacKenzie R. Patients' perceptions of magnetic resonance imaging. / R. MacKenzie [et al.] // Clinical Radiology. – 1995. – Vol.50, №3. – P. 137–143.
- Szameitat A.J. The functional magnetic resonance imaging (fMRI) procedure as experienced by healthy participants and stroke patients – A pilot study / A.J. Szameitat, S. Shen, A. Sterr // BioMed Central Medical Imaging. – 2009. – Vol.9, №14. – P. 1–11.
- Grey S.J. Reduction of anxiety during MR imaging: a controlled trial / S.J. Grey, G. Price, A. Mathews // Magnetic Resonance Imaging. –2000. – Vol.18. – P. 351 – 355.
- Henson R. Efficient experimental design for fMRI / R. Henson // Statistical Parametric Mapping: The analysis of functional brain imaging data. – Academic Press, 2006. –P. 193–210.
- Maus B. Optimization of blocked designs in fMRI studies / B. Maus [et al.] // Psychometrika. – 2010. – Vol.75, №2. – P. 373–390.
- Holmes A.P. Characterizing brain images with the general linear model. / A.P. Holmes, J.B. Poline, and K.J. Friston // Human Brain Function. – Academic Press, 1997. – P. 59–84.
