APPLICATION OF THE ITERATIVE METHODS OF SYSTEMS OF LINEAR ALGEBRAIC EQUATIONS SOLUTIONS FOR MULTI-CHANNEL INFORMATION SYSTEMS ANALYSIS

Пакляченко М.Ю.

Адъюнкт кафедры информационной безопасности, Воронежский институт МВД России

ПРИМЕНЕНИЕ ИТЕРАЦИОННЫХ МЕТОДОВ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ ДЛЯ АНАЛИЗА МНОГОКАНАЛЬНЫХ СИСТЕМ ОБРАБОТКИ ИНФОРМАЦИИ

Аннотация

В статье проводится обзор итерационных методов решения систем линейных алгебраических уравнений. Приводятся необходимые и достаточные условия сходимости методов. Обосновывается выбор оптимального метода решения с учетом определенных требований. Предложенный анализ представляет интерес для  математического моделирования многоканальных систем.

Ключевые слова: метод простых итераций, сходимость, устойчивость, система линейных алгебраических уравнений.

Paclyachenko M.Y.

Post-graduate cadet of the Information Security chair, Voronezh Institute of the Ministry of the Interior of Russia.

APPLICATION OF THE ITERATIVE METHODS OF SYSTEMS OF LINEAR ALGEBRAIC EQUATIONS SOLUTIONS FOR MULTI-CHANNEL INFORMATION SYSTEMS ANALYSIS

Abstract

The article reviews iterative methods of solution systems of linear algebraic equations is spent. The required  and adequate conditions for the convergence of methods are resulted. The choice of the optimal method of solution with specified requirements is proved. The suggested analysis is significant to the mathematical modeling of multi-channel systems.

Key words: iteration, method of simple iterations, convergence, constancy, system of linear algebraic equations, matrix.

Для решения задач обработки информации в случае изменяющейся во времени интенсивности потоков данных P(t), в особенности наличия пиковых выбросов, применяют многоканальные системы с резервированием. При обработке информации в многоканальных системах c параллельным включением каналов важными характеристиками системы является быстродействие (скорость перераспределения информации между каналами) и устойчивость к динамическим перегрузкам.

Математическое моделирование информационных систем такого рода может осуществится на основе систем линейных алгебраических уравнений (СЛАУ), в матрице коэффициентов которой элементы главной диагонали отражают свойство изоморфности канала, а остальные элементы - взаимосвязи между каналами, определяющие быстродействие подсистемы распределения информации между каналами (диспетчеризация) и устойчивость к динамическим нагрузкам.

Скорость сходимости решения СЛАУ может характеризовать быстродействие многоканальной системы, а устойчивость сходимости - реакцию системы на динамические перегрузки. Дополнительным достоинством СЛАУ как прототипа математической модели многоканальной системы являются возможность учета неоднородностей каналов и взаимосвязей между ними в значениях соответствующих коэффициентов.

В связи с этим итерационные методы (ИМ) решения СЛАУ представляют интерес для анализа многоканальных систем, поскольку пошаговое воспроизведение процедур с получением промежуточных решений может отождествляться с динамической реакцией системы.

Итерационные методы решения характеризуются тем, что при их реализации точное решение системы представляется как предел некоторой бесконечной последовательности векторов (приближений). Простота вычислительных схем и однообразие производимых операций делают эти методы удобными при использовании вычислительной техники для решения СЛАУ, описывающих некоторые информационные процессы (например, обработка или передача информационных потоков) в информационных системах.

Одно из значимых свойств таких методов решения – самоисправляемость [3]. При их использовании отдельный сбой в вычислениях не приведет к ошибкам в окончательном результате, он может лишь увеличить число проводимых итераций. Так же преимущество итерационных методов перед точными состоит в том, что они позволяют достичь решения с заданной точность гораздо быстрее. Кроме того, они применимы для решения СЛАУ больших размерностей (порядка 10⁷).

В зависимости от применяемого подхода ИМ могут быть основанными на расщеплении, вариационного типа, проекционного типа. Примером итерационных методов, основанных на расщеплении, могут служить метод простых итераций (МПИ), метод Якоби, метод Зейделя и др. К классу вариационных ИМ относят метод минимальных невязок, метод скорейшего спуска и т.д.

Существенными характеристиками ИМ являются сходимость и устойчивость. ИМ будет сходящимся, если для любого начального приближения можно построить последовательность, сходящуюся к точному решению уравнения. Таким образом, сходимость определяется близостью получаемого численного решения задачи к истинному решению. Устойчивость представляется как особенность вычислительного процесса, заключающаяся в росте промежуточных значений и в накоплении ошибок округления. При устойчивом методе малое приращение исходных данных приводит к малому изменению искомых.

Метод простой итерации

Практически вычислять простые итерации СЛАУ вида 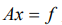можно двумя способами.

1) по формуле:

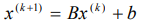,                                                                                                                               (1)

компоненты последующего приближения находятся суммой матрицы перехода, представленной разностью единичной и исходной  матриц, умноженных на начальное приближение, и столбца свободных членов. Начальное приближение можно выбирать произвольно (обычно в качестве 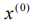 выбирают столбец свободных членов b). Здесь каждое найденное приближение рассматривается как исходное. Это придает МПИ самоисправляющийся характер, но недостатком этого может быть больше количество проводимых итераций.

2) по формуле:

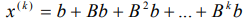.                                                                                                   (2)

Такая организация удобна своим единообразием процесса, и тем, что каждое слагаемое этой суммы является лишь поправкой к найденному приближению. Но при этом самоисправляемость теряется, возникает чувствительность к случайным ошибкам, накопление ошибок при округлении от возрастания числа слагаемых.

Судить о сходимости метода можно при помощи достаточных признаков, связанных непосредственно с самой матрицей перехода и ее элементами.

Теорема 1: для того, чтобы МПИ сходился при любом начальном приближении, необходимо и достаточно, чтобы все собственные значения матрицы перехода были по модулю меньше единицы.

Теорема 2: для того, чтобы МПИ сходился, достаточно, чтобы какая-либо норма матрицы  была меньше единицы (фактически это следствие теоремы 1).

Теорема 3: для того, чтобы МПИ сходился, достаточно, чтобы матрица системы обладала преобладанием диагональных элементов [1].

Скорость сходимости  определяют оценки погрешности метода. Сравнить точность двух последовательных приближений можно по формуле:

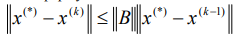.                                                                                                     (3)

Касательно вычислительной неустойчивости, можно отметить, что метод является устойчивым, при соблюдении достаточного условия сходимости. В этом случае, он так же будет самоисправляющимся, т.е отдельная ошибка в вычислении новых приближений не отразится на результате, т.к ошибочное приближение всегда можно рассматривать за начальное.

Метод Якоби

Данный метод является модификацией МПИ, работающей на матрице перехода, приведенной к специальному виду путем деления уравнений на диагональные элементы матрицы системы.

Так как метод Якоби представляет собой модифицированный МПИ, с априорным выполнением требования теоремы 3 то для осуществления сходимости требуется выполнение условий теоремы 1 или теоремы 2.

Скорость сходимости, исходя из определения точности, будет зависеть от нормы матрицы перехода.

Метод Некрасова

Этот метод является модификацией рассмотренного выше метода, которая заключается в определенном преобразовании матрицы системы. Производится ее разложении на диагональную и треугольные матрицы, в одной из которых элементы, стоящие выше главной диагонали и на ней равны 0, а остальные численно равны соответствующим элементам матрицы системы, в другой треугольной матрице – наоборот: элементы ниже главной диагонали и стоящие на ней – нули, а стоящие выше численно равны элементам а_ij.

Для того, чтобы метод Некрасова сходился при любом начальном приближении необходимо и достаточно, чтобы все собственные значения матрицы перехода были по модулю меньше единицы. Т.о характер сходимости и ее скорость рассматриваемого метода аналогичны рассматриваемым характеристикам  порождающего метода.

Метод Зейделя

Данный метод - модификация МПИ, в итерационном процессе которого,  при вычислении последующих координат вектора x^(k+1) используются уже найденные компоненты этого вектора.

При реализации данного ИМ производится расщепление на диагональные матрицы не матрицы системы (как в методе Некрасова), а матрицы перехода, причем первая из расщепляющих треугольных матриц (элементы, стоящие выше главной диагонали и на ней, которой равны нулю) коммутирует с найденными компонентами искомого вектора.

Области сходимости метода Зейделя и МПИ различны. Для того, чтобы метод Зейделя сходился необходимо, чтобы норма произведения матрицы расщепления и второй треугольной матрицы  была меньше 1. Проверка этого условия затруднительна. Для ускорения сходимости метода Зейделя применяют ускоряющие коэффициенты, определяющие иной ИМ - метод релаксации [2].

Метод релаксации

Метод релаксаций  содержит свободный параметр, изменяя который можно получать различную скорость сходимости итерационного процесса.

Согласно методу Зейделя компоненты вектора х^(k+1) вычисляются в строго определенном порядке, определенном порядком следования компонент. Так как все компоненты вектора равноправны, то можно начинать вычисления с любой компоненты, при этом порядок нахождения компонент можно подчинить какому-нибудь разумному принципу. Например, в первую очередь можно исправлять ту компоненту решения, которая хуже найдена, чтобы при нахождении других компонент участвовало уже улучшенное ее значение. Эта идея ослабления влияния «плохой» компоненты может быть осуществлена по-разному.

О точности приближенного значения можно судить по величине вектора ошибки, однако, этот вектор невозможно вычислить, не зная точного решения. Поэтому иногда прибегают к вектору, который отражает разность между приближением на определенном шаге и предшествующем ему приближением, вычисляемым по формуле:

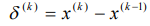.                                                                                                                              (4)

Тогда при нахождении вектора 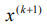 вычисляют его компоненты в порядке убывания модулей компонент вектора 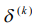, т.е первой находится та компонента вектора 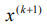, номер которой совпадает с номером максимальной по модулю компоненты вектора .

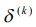О точности релаксационного метода можно судить по вектору ошибки или вектору невязки. Условие сходимости определяется так: если в процессе релаксации для системы с положительно определенной матрицей выполнены условия такие что, последовательность ведущих индексов 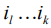 имеет интервал повторяемости и множители релаксации  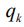удовлетворяют условию формулы:

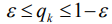.                                                                                                                                                       (5)

Учитывая вышесказанное, можно сделать следующие выводы. Итерационные методы позволяют построить последовательность приближенных решений СЛАУ. Их значащими характеристиками являются сходимость, скорость сходимости и устойчивость.

В основе построения всех ИМ лежит принцип перехода от системы к ее эквивалентному виду. Отличие конкретного итерационного метода заключается в выборе матрицы перехода.

Общее условие сходимости матричной прогрессии в методах состоит в том требовании, чтобы все собственные значения матрицы были по модулю меньше единицы. Однако в каждом методе к этому требованию могут присоединяться  дополнительные (обусловленные, например, матрицами перехода и расщепления).Скорость сходимости метода будет зависеть от максимального значения собственного числа матрицы перехода. Чем меньше норма матрицы – тем быстрее сходимость метода. Кроме того, о ней можно судить и по оценкам погрешности.

Базисным можно считать МПИ. Его модификациями являются методы Якоби и Зейделя, метод Некрасова является модификацией метода Якоби, и соответственно МПИ. Релаксационный метод – фактически улучшенный и модифицированные метод Зейделя, и соответственно так же является модификацией МПИ.

Из рассмотренных методов оптимальным с точки зазрения минимизации ошибки и улучшения скорости сходимости является метод релаксации, однако он требует затрат на определение вектора невязки и порядка изменения компонент искомого вектора для решения. В методах Зейделя и Некрасова при определении скорости сходимости может возникнуть проблема нахождения собственных значений. Метод Якоби эффективен в случае диагонального преобладания элементов системы, однако он, так же как и методы Зейделя, Некрасова, Релаксации требует расщепления исходной матрицы, что влечет за собой затрату ресурсов и вычислительного времени на воспроизведение данных действий. По сложности методы, предложенные Якоби и Зейделем, одинаковы, однако если итерационный процесс может проводиться как в виде итераций Якоби, так и в виде итераций Зейделя, то последний в этом случае предпочтительней по причине улучшения сходимости.

Метод простой итерации уступает другим в точки зрения скорости сходимости, однако он не требует преобразований матрицы системы, имеет простые, в смысле реализации, требования к сходимости итерационного процесса. Кроме того, в случае, если важна наглядность процесса решения, он является наиболее удобным для реализации программным способом пошагового воспроизведения результатов текущей итерации. Реализация данного метода предпочтительна с точки зрения возможности проведения исследований в зависимости от параметров задачи (размерности матриц) касающихся устойчивости и сходимости метода, влияния повышения точности решения и числа необходимых итераций, влияния начального приближения, изменения коэффициентов матрицы перехода.