DETERMINING THE COMPRESSION RATE AND QUALITY OF RESTORED IMAGES BASED ON PREDEFINED PARAMETERS

В настоящее время задача передачи изображений по каналам связи является актуальной. При этом существуют классы задач, в которых точное сохранение визуальной составляющей не обязательно, допустимы некоторые отклонения от исходного качества, не влияющие на общее восприятие изображения. Однако в подобных задачах более весомы такие критерии как затраты времени работы и памяти вычислительных устройств на передачу изображения, нагрузка на канал связи, объём передаваемой информации.

Разработано множество методов сокращения информационной избыточности неподвижных изображений

– ортогональные преобразования, основанные на системах непрерывных функций (синусоидальных или вейвлет-функций), дающие характерные эффекты при обработке дискретных сигналов;

– вычисления с плавающей точкой, накладывающие дополнительные ограничения на архитектуру и аппаратные требования к вычислительным системам передачи изображений;

– методы энтропийного кодирования, эффективно реализующие сокращение избыточности данных, заранее подготовленных на предыдущих этапах, однако требующие создания, а также хранения или передачи дополнительной информации в виде словарей, без которых невозможно кодирование и декодирование данных.

Эти и другие подходы к разработке алгоритмов сжатия существенно усложняют процесс передачи изображений в системах с аппаратными и энергетическими ограничениями на передающее оборудование

Авторам и были предложены алгоритмы сжатия и протоколы передачи данных, основанные на применении теории дискретных сигналов, определённых на конечных интервалах

Для известных и стандартизированных алгоритмов существуют критерии, изменение которых позволяет получить предсказуемый результат в смысле некоторых характеристик, например, качества или степени сжатия. Так, качество восстановленного изображения в алгоритме JPEG задаётся выбором соответствующих таблиц квантования

В работе предполагается, что изображение представлено матрицей яркостей пикселей I, размер матрицы N*N, N = 2n, n – натуральное число. Значение яркости пикселя находится в диапазоне от 0 до 255, где 0 соответствует чёрному цвету, 255 – белому.

В исследуемых алгоритмах основной является идея перехода к квазидвумерному спектральному пространству, которое может быть представлено как (1):

(1)

где B – матрица квазидвумерного спектра изображения, W – матрица функций Уолша, упорядоченная по Уолшу. При работе с функциями Уолша применяются термины обобщённой частоты или частости (секвенты) в качестве указания отличия их от частот, получаемых в результате преобразования Фурье и других преобразований, основанных на синусоидальных функциях

В описанных раннее алгоритмах исключение «высокочастотных» составляющих квазидвумерных спектров изображения задавалось пороговым значением k.

Задание значения исключения составляющих одним числом имело ряд неудобств. Во-первых, число k приходилось подбирать многократно отдельно для каждого изображения для получения данных с фиксацией результатов по другим критериям, таким как степень сжатия или качество изображения. Во-вторых, значение k – это значение уровня составляющих, все элементы спектра, по модулю меньшие k, исключаются, то есть становятся равными 0 (2).

(2)

Подобное число имеет смысл в исследуемой области, однако для пользователей алгоритма более понятными могут являться иные критерии, например, процент исключённых составляющих.

Новый подход к исключению составляющих учитывает указанные замечания и заключается в реализации следующих шагов:

1. Задаётся пороговое значение k, имеющее заранее довольно высокое значение (при исключении составляющих по данному порогу будет устранено около 90% спектра).

2. Задаётся процент исключённых составляющих p, который будет означать предельную долю возможных исключённых элементов спектра.

3. Исключение составляющих по заданному порогу начинается с области высоких частот и продолжается до тех пор, пока не будет достигнут заданный процент p или (если процент недостижим в принципе) не будут исключены все составляющие ниже порога.

Пусть количество спектральных составляющих, которые надо исключить для достижения процента p равно , а текущее количество исключённых составляющих равно q. Тогда исключение составляющих спектра, обеспечивающее заданную степень сжатия, может быть выражено как (3):

(3)

При этом . Такой порядок обхода матрицы позволит начать исключение компонентов спектра с области концентрации компонентов высокой частости при упорядочении матрицы преобразования по Уолшу, что позволит обеспечить более высокую степень сжатия по сравнению с обходом с области низких частостей.

Предложенный подход позволит применять более наглядный критерий исключения составляющих, при этом процент исключённых составляющих будет отражать примерную степень сжатия.

Одним из критериев оценки качества восстановленного после сжатия изображения является среднеквадратическое отклонение (СКО, англ. Root-mean-square error, RMSE) восстановленного изображения от исходного (4):

(4)

где I* – матрица восстановленного после сжатия изображения.

Для попытки оценить качество восстановленного изображения после исключения составляющих квазидвумерного спектра рассмотрим, как связано СКО изображений и их квазидвумерных спектров.

СКО квазидвумерных спектров можно представить как (5)

(5)

Так как разницу между спектрами составляют только исключённые значения, то выражение (4) можно переписать как (5)

(6)

где  – матрица исключённых составляющих. Тогда выражение (4) можно представить в виде (7):

(7)

где  – матрица разностей яркостей пикселей исходного и восстановленного изображений.

Исходя из равенства Парсеваля для квазидвумерных спектров

(8)

 можно получить следующее выражение (9):

(9)

Учитывая (6), получим (10):

(10)

Таким образом, чтобы добиться заданного качества восстановленного изображения, предлагается задать достаточно высокий порог k (по тому же принципу, что и в предыдущем критерии) и RMSEI, и исключать из спектра его компоненты до тех пор, пока сумма квадратов значений этих компонентов не достигнет заданной суммы, рассчитанной с помощью (10).

Пусть а текущая сумма квадратов исключённых элементов равно D. Тогда исключение составляющих спектра, обеспечивающее заданное СКО, может быть выражено как (11):

(11)

При этом  

Исходя из (10), можно предположить, что значения D и S могут занимать более 8 десятичных разрядов, и квадрат каждого исключаемого компонента, близкого по модулю к k будет вносить большой вклад в результирующее СКО. Исходя из этого предлагается ввести некоторую окрестность , в пределах которой будет производиться расчёт суммы квадратов (12).

(12)

Представленный подход позволит более точно получить требуемое качество изображения по сравнению с исключением составляющих только по порогу k (2).

Экспериментальная проверка предложенных критериев проводилась на наборе ландшафтных изображений, имеющих различную тематику: лесная местность, сельская местность, городская застройка.

На рисунке 1 изображены графики степени сжатия изображений при использовании предложенных критериев прореживания.

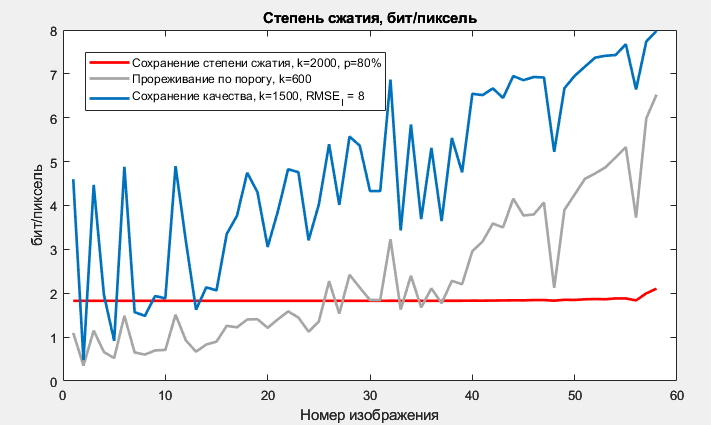
Рисунок 1 - Степень сжатия изображения при использовании предложенных критериев прореживания

DOI:10.60797/IRJ.2024.150.80.1

Красным цветом изображён график способа прореживания, при котором получены результаты, отличающиеся наименьшей дисперсией степени сжатия Dbpp (13) (таблица 1), а значит, предсказуемостью результатов в смысле степени сжатия.

(13)

где K – количество проведённых экспериментов, X – вектор полученных степеней сжатия,  – среднее значение степени сжатия в K экспериментах.

На рисунке 2 изображены графики качества восстановленных изображений при использовании предложенных критериев прореживания.

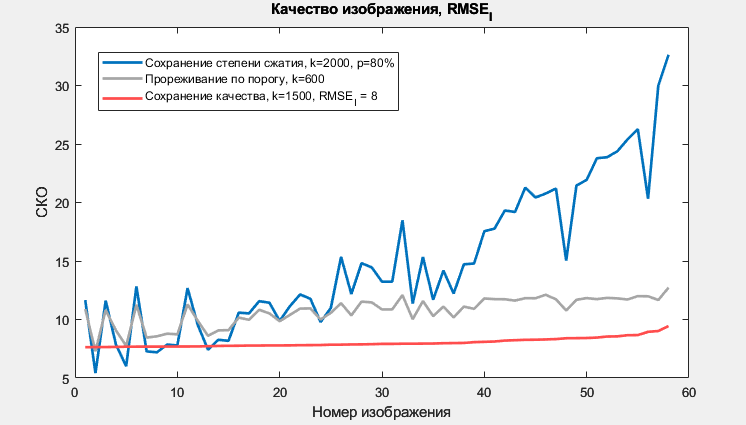
Рисунок 2 - СКО изображений при использовании предложенных критериев прореживания

DOI:10.60797/IRJ.2024.150.80.3

Красным цветом изображён график способа прореживания, при котором получены результаты, отличающиеся наименьшей дисперсией DRMSE (таблица 2), а значит, предсказуемостью результатов в смысле качества восстановления. DRMSE была рассчитана аналогично Dbpp (13).

Пример сжатия изображения из исходного набора данных изображён на рисунке 3.

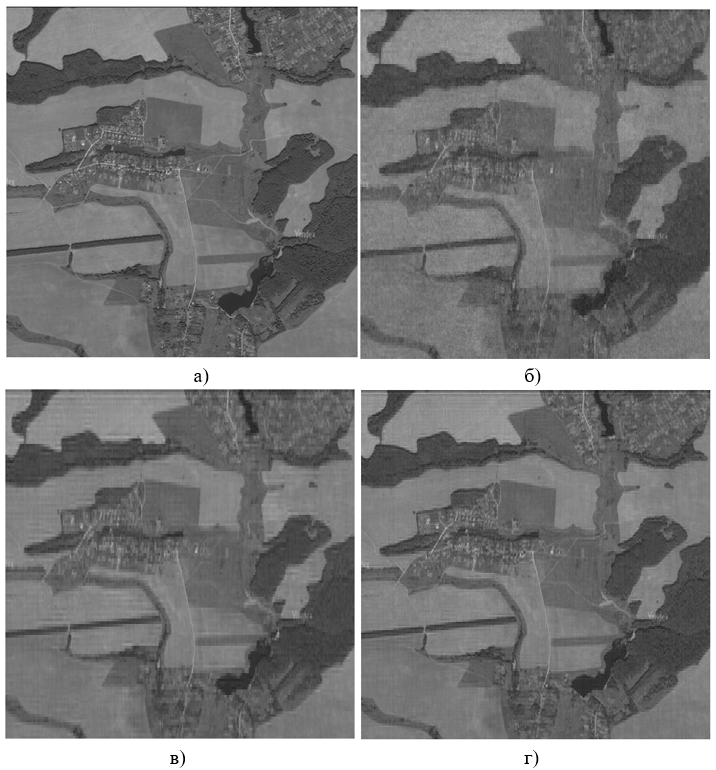
Рисунок 3 - Пример сжатия изображения: 

а - исходное изображение; б - прореживание по порогу, k=600; 1,1249 бит/пиксель; СКО = 10,0018; в - сохранение степени сжатия, k=2000; p=80%; 1,8277 бит/пиксель; СКО = 9,7841; г - сохранение качества, k=1500; = 8; 3,2 бит/пиксель; СКО = 7,8164

DOI:10.60797/IRJ.2024.150.80.5

Результат рисунка 3 в) показывает, что при p=80% произошло сжатие с 8 до 1,8277 бит/пиксель, на 77%. На рисунке 1 г) заданное СКО было равно 8, полученное после сжатия СКО равно 7,8164.

Таким образом, предложенные критерии способны обеспечивать заранее заданные степень сжатия и качество восстановленных изображений.

Для задачи сжатия изображений с использованием квазидвумерного спектрального представления в базисе функций Уолша выведены критерии прореживания, обеспечивающие заранее заданную степень сжатия и СКО.

В экспериментальной части демонстрируется работоспособность предложенных критериев при сжатии ландшафтных изображений.

Разработанные критерии исключения составляющих спектров могут быть обобщены для других видов ортогональных преобразований; критерий восстановления, обеспечивающий качество изображений, в дальнейшем может быть получен для других рассчитываемых метрик оценки качества изображений.

Областью применения разработанных критериев являются задачи сжатия и изображений в условиях ограничений на аппаратные характеристики оборудования обработки и передачи данных.