Parallelization of the ant-pollinator method for the survival analysis model building problem
Parallelization of the ant-pollinator method for the survival analysis model building problem
Abstract
Prognostic models play a key role in decision-making in various scientific and applied areas, allowing to predict the outcome of events based on the input parameters of the studied object. One of such areas is survival analysis – a set of statistical methods designed to estimate the probability of occurrence of terminal events. The paper addresses the problem of building predictive models based on a hybrid metaheuristic ant-pollination algorithm. The efficiency of parallelization of this algorithm is examined, which allows to reduce the computational time in training the models. The work demonstrates that the proposed survival analysis model building method can be effectively parallelized. Parallelization speeds up the model training process, which is especially important when intermediate models are repeatedly trained. Experiments show that the dependence of parallelization efficiency on the number of computational nodes is non-linear: increasing the number of nodes increases the speed of the algorithm, but with a certain limit. The results show that parallelization on a few computational nodes is the most effective in terms of reducing computation time.
1. Введение
Прогностические модели играют важную роль в принятии решений в различных прикладных научных областях. Прогностические модели позволяют предсказать исход некоторого события по входным параметрам исследуемого объекта. Одним из ключевых направлений среди таких моделей является анализ выживаемости. Это набор статистических методов, которые позволяют оценить вероятность наступления терминального события, после которого объект перестает подлежать наблюдению. Анализ выживаемости применяется для моделирования и исследования распределения времени до наступления терминальных событий
. Модели и методы анализа выживаемости используются в медицине , биотехнологии , а также в прикладных задачах экономики и социологии .Важной задачей является выбор и построение моделей по набору данных. Построение таких моделей возможно с помощью гибридных метаэвристических алгоритмов
, одним из которых является алгоритм муравьев-опылителей. Задача построения модели является затратной по времени и ресурсам, так как алгоритм требует обучения модели при каждом найденном решении. Цель работы – исследование эффективности распараллеливания алгоритма муравьев-опылителей. Параллельная реализация позволяет сократить время построения модели, что является актуальным с точки зрения практического приложения алгоритма.2. Методы и принципы исследования
2.1. Задача
Метод муравьев-опылителей позволяет строить функцию риска для модели анализа выживаемости по исходному набору данных.
Определим – как набор входных данных, используемых для обучения модели. Зададим множество признаков
.
– подмножество признаков:
.
Зададим произвольную функцию риска для модели с функциональным ядром
, обученной на наборе данных
и с множеством признаков
в виде:
Для оценки качества модели используется c-индекс
.Задача – распараллелить алгоритм , входными данными которого являются набор данных
и множество признаков
, а результатом работы – модель
:
Функция риска является обобщением функции риска модели Кокса. При функция риска становится идентичной функции риска регрессионной модели Кокса.
2.2. Метод муравьев-опылителей
Метод муравьев-опылителей основан на гибридном методе муравьиной колонии и способен решать задачу построения функции выживаемости моделей анализа выживаемости
. Особенность алгоритма заключается в преобразовании множества вершин графа, которые представляют признаки или их комбинации в модели. Он имитирует процесс опыления цветковых растений с помощью насекомых-опылителей. Алгоритм состоит из трех компонентов: муравьиного алгоритма, который используется для построения модели; генетического алгоритма, предназначенного для оптимизации работы муравьиного алгоритма; и алгоритма опыления, который применяется для выбора признаков или их сочетаний.Результатом работы алгоритма является расширенная модель Кокса, функцией риска которой является построенный полином :
,
где – множество всех битовых векторов, каждый элемент которого – индикатор вхождения
-го признака в
-е слагаемое полинома,
– маркер, указывающий вхождение
-го монома в
.
Ядро функции риска связано с полиномом следующим образом:
Идея алгоритма заключается в следующем. Каждый моном из представлен в алгоритме цветком. Множество цветов образует граф, путь по которому строят муравьи-опылители. Каждый муравей составляет множество цветов, сумма соответствующих мономов которых образует полином
.
Муравьиный этап алгоритма использует идею простого муравьиного алгоритма
, в котором переопределены правила откладывания феромона и выбора вершин в соответствии со спецификой задачи . Вторым этапом гибридного алгоритма является приложение генетического алгоритма, используемого для оптимизации параметров муравьиного этапа.Этап опыления основан на популяционной концепции и реализуется через применение четырех операторов к популяции цветков: селекции, кроссбридинга, лайнбридинга и старения. Каждый цветок имеет параметр – возраст. Оператор селекции выбирает цветы с наибольшей концентрацией феромонов. Оператор кроссбридинга с определенной вероятностью создает новые цветы, чьи мономы составлены из мономов цветов-предков. Оператор лайбридинга добавляет случайным образом в популяцию моном с единичным признаком, а оператора старения повышает возраст каждого из цветов. Если возраст цветка переступит некоторый порог, цветок погибает.
Алгоритм можно представить в виде шагов:
Начало
1. Определить параметры
2. Положить
3. Положить множество цветов:
4. Положить множество муравьев
5. Пока не достигнут критерий остановки:
5.1. Для каждого муравья :
5.1.1.
5.1.2.
5.1.3.
5.1.4. Пока :
5.1.4.1. Выбрать в соответствии с правилом выбора вершины
5.1.4.2.
5.1.4.3.
5.1.4.4.
5.1.4.5.
5.1.5. Если :
5.1.5.1.
5.1.5.2.
5.1.6. Для каждого вычислить
5.2. Применить оператор выбора
5.3. Применить оператор кроссинговера
5.4. Применить оператор мутации
5.5. Применить оператор селекции цветов
5.6. Применить оператор кроссбридинга
5.7. Применить оператор лайнбридинга
5.8. Применить оператор старения
6. Вернуть значения
Критерием остановки алгоритма может являться количество итераций или сходимость решений к одному значению.
2.3. Распараллеливание метода
Одним из преимуществ многих метаэвристических алгоритмов является возможность их распараллеливания. Существует несколько способов оценивания распараллеливания.
Параллельное ускорение – это отношение скорости выполнения программы на нескольких вычислительных узлах к скорости выполнения программы на одном вычислительном узле (1):
где – средняя скорость выполнения программы на p кластерах.
Также используется другой показатель, который позволяет получить оценку эффективности распараллеливания с учётом количества вычислительных узлов – параллельная эффективность (2):
Чем ближе к единице, тем эффективнее является распараллеливание
Известно, что муравьиные алгоритмы имеют параллельную реализацию
, так как поиск решения отдельного муравья одной итерации не зависит от результатов поиска других муравьев. Поэтому муравьиные алгоритмы эффективно распараллеливаются по данным. Однако рассматриваемый метод является гибридным, а значит, существует возможность появления новых зависимостей, не поддающихся распараллеливанию. Так как в рассматриваемом алгоритме наиболее затратным действием является обучение модели, оно положено за единицу вычисления для определения скорости выполнения программы вСхема распараллеливания алгоритма муравьев-опылителей представлена на рисунке 1.
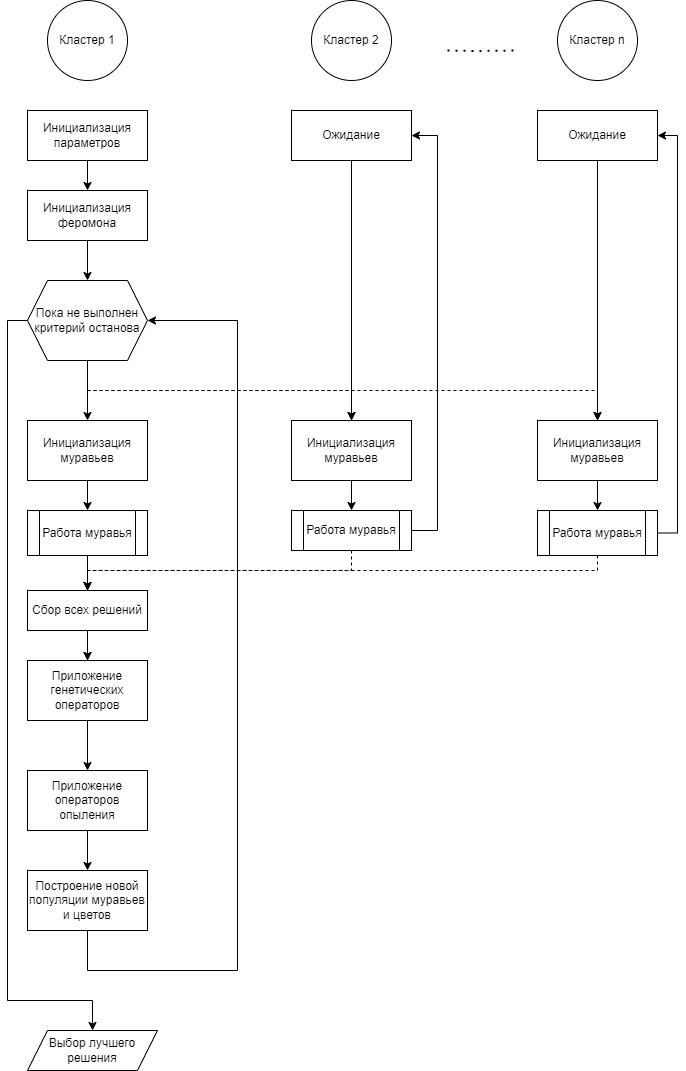
Рисунок 1 - Схема распараллеливания алгоритма муравьев-опылителей
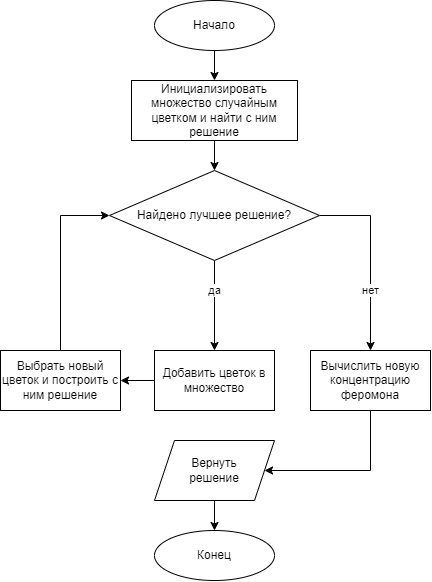
Рисунок 2 - Блок-схема операций, которые совершает муравей
3. Основные результаты
Распараллеливание осуществлялось с помощью MPI, стандартного интерфейса программирования для написания параллельных программ на кластерных компьютерах. Программа была запущена 50 раз при различных конфигурациях с разным количеством потоков.
В таблице 1 представлены результаты распараллеливания алгоритма муравьев-опылителей, в которой отражены время, скорость выполнения программы, а также оценочные характеристики.
Таблица 1 - Результаты распараллеливания алгоритма муравьев-опылителей на базе данных больных раком предстательной железы
Количество потоков | Среднее время выполнения алгоритма, с | Скорость выполнения программы | Параллельное ускорение | Параллельная эффективность |
1 | 38,254 | 3,673 | 1 | 1 |
2 | 28,560 | 5,225 | 1,423 | 0,711 |
3 | 26,219 | 6,149 | 1,674 | 0,558 |
4 | 21,300 | 6,970 | 1,898 | 0,474 |
6 | 21,018 | 7,273 | 1,980 | 0,330 |
12 | 19,279 | 8,099 | 2,205 | 0,184 |
Тестирование проводилось на базе данных больных раком предстательной железы, наблюдавшихся, либо получавших лечение в ФГБУ «РНЦРХТ им. ак. А.М. Гранова» Минздрава России в период с января 1996 по декабрь 2016 года
. В исследование включены обезличенные данные 5073 пациентов, у которых была доступна информация о степени распространенности опухолевого процесса.4. Обсуждение
Параллельное ускорение и параллельная эффективность в таблице 4 вычислены по формулам (2) и (3) соответственно. Из результатов распараллеливания видно, что дополнительные кластеры ускоряют работу выполнения программы, однако зависимость ускорения нелинейная. С увеличением количества кластеров уменьшается приток ускорения и снижается параллельная эффективность. Следовательно, алгоритм может быть распараллелен, однако вследствие того, что алгоритм имеет последовательную часть, рост параллельного ускорения с возрастанием количества кластеров снижается.
5. Заключение
Таким образом продемонстрировано, что предложенный метод построения моделей анализа выживаемости с выбором признаков может быть распараллелен. Распараллеливание является важной задачей, так как время обучения модели является затратным, а обучение промежуточных моделей происходит неоднократно.
Распараллеливание программы представлено нелинейной зависимостью как времени, так и скорости работы, от числа кластеров. С увеличением числа вычислительных узлов эффективность распараллеливания снижается. Запуск работы алгоритма на двух вычислительных узлах увеличил скорость работы алгоритма в 1,423 раза; на шести вычислительных узлах – в 1,98 раза; на двенадцати – в 2,205. Это показывает целесообразность распараллеливания алгоритма на сравнительно небольшом количестве вычислительных узлов.
