QUANTUM VEHICLE TAKE-OFF MODELLING
QUANTUM VEHICLE TAKE-OFF MODELLING
Abstract
The prospect of introduction of quantum cars, using the thrust of quantum engine-driver (QED), implemented in the pitch plane, leads to the need to consider the possibilities and features of take-off of these cars. The analogues can be aircraft vehicles (AV). In the absence of full-scale vehicles with QED, the study relies on software simulation modelling (SSM), flexible model and powerful software.
Two related problematic conflicts are addressed:
1) against the background of automotive and AV-analogues – the change in the structure and role of the lifting force in the implementation of the lift of the quantomobile;
2) providing a continuum of multiple take-off strategies, from aeroplane acceleration variant to helicopter vertical take-off.
The objectives of the development were: creation of a subsystem of take-off and diverted motion (TDM) in the author's Quantomobile Ground Motion Model (QGMM); elaboration of the interface of interaction with the model; conducting SSM on the basis of TDM with experiments covering a number of variants of vehicle take-off.
An algorithm for taking off and hovering of a quantum vehicle is developed. The algorithm is implemented in the Simulink-modelling environment. The formed model allows to trace trajectories of changes in dynamic parameters during SSM of the quantomobile take-off processes. Graphical capabilities of Matlab software were used.
In a series of calculations of acceleration and suspension of the quantomobile to the designated altitudes under different scenarios of changes in the magnitude and slope angles of the trust vector, air resistance and lift force, rolling resistance on the OP and other factors, the strategies and variants of the quantomobile take-off were evaluated, and a framework of reference take-off trajectories was formed.
The TDM subsystem developed in the QGMM environment allows to carry out a computational study of the vehicle motion in the pitch plane. On the basis of the calculations and their analyses carried out by means of TDM with QGMM the cognitive complexity of formation of trajectories of motion of a quantum car at the stage of its take-off in the interrelation of trust and aerodynamic lifting forces is overcome. The presence of trust lifting force of QDD is a unifying factor in the synthesis of CTOL, STOL and VTOL take-off methods covered by a single algorithm. The QGMM is regarded as a basis for further development of modelling of quantum vehicle motion under arbitrary conditions.
1. Введение
На базе идей извлечения энергии из физического вакуума (ФВ)
, , в современной физике рассматриваются концепции квантовых двигателей (КД), генерирующих направленный траст (тягу) за счет определенной деформации поля ФВ , . Примером могут быть разработки российского ученого Леонова В.С. , . Надежда на практическую реализацию названых идей и концепций становится все более существенной , .Реализация идеи КД приведет к появлению нового типа транспортных средств (ТС) – квантомобилей
, , . Станет возможным прикладывать траст КД к корпусу экипажа (в конструктивно обусловленной точке) непосредственно (без трансмиссии). Необходимость трансмиссии отпадет, колесам (при наземном движении) останется только опорная функция.При возможности шарнирного (сферического) обметания вектора траста
, появляются его вертикальная и боковая компоненты, которые можно будет использовать для вывешивания (лифта) и бокового движения квантомобиля. Горизонтальная компонента траста при этом используется для преодоления сил сопротивления продольному движению экипажа , , (здесь и везде далее используем слово «экипаж» в смысле «коляска», но не команда). КД, с реализацией таким образом функций движителя ТС, становится силовой установкой типа Квантовый двигатель-движитель (КДД). В этой статье, однако, ограничимся рассмотрением действий КДД и экипажа в целом только в продольной плоскости тангажа.Автор ранее рассматривал концепции механики ТС с КДД
, , , . Причем, концепции охватывали, с одной стороны, возможность моделирования всесредного мультимодального квантомобиля (ВМК) , , , а с другой стороны, – моделирование смежных мобильных ТС: портовых и карьерных транспортеров, поездов . В монографии предложено в широкое понимание термина квантомобиль включать весь набор мобильных ТС с КДД (не только производное средство от «автомобиль»).В рамках продольного движения квантомобиля в плоскости развёртывания угла тангажа β вектор траста FT раскладывается на две ортогональные компоненты FTx и FTz , :
В скалярной записи это:
Угловой диапазон обметания вектора траста в общем случае составляет от 0° до 360°; взлет экипажа описывается в квадранте I (от 0° до 90°).
Рассмотренные концепции находятся в основе развиваемой авторской Simulink-модели приземного движения квантомобиля (МПДК)
.В публикациях
, , на базе МПДК рассмотрена методика и даны примеры расчета тяговых сил квантомобилей для наземной среды движения ТС с возможным переходом в воздушную среду. Показывается, что расчетная методика, в связи с необходимостью учета лифта, отличается от традиционных алгоритмов расчета силового баланса автомобиля.В работах
, , автором рассматривались вопросы продольной устойчивости квантомобиля. В работе обосновывались требования к энергетической цене тяги КДД, которые позволят квантомобилю превосходить современные ТС по энергоэффективности. Эти аспекты несомненно потребуют их привлечения к формированию комплексных оценок эффективности передвижения средств квантомобильного транспорта.В данном исследовании, однако, сосредоточимся на механике неизведанного траекторного аспекта движения квантомобиля – его взлете. Решение задачи траекторного исследования допускает избежания рассмотрения устойчивости объекта и энергетики процесса, но вместе с тем способно обеспечить будущую оптимизацию в поле возможных траекторий взлета (уже с привлечением показателей устойчивости и критериев энергоэффективности) каркасом опорных траекторий и фиксированными операционными точками
.Взлёт объекта становится возможным только тогда, когда суммарная подъёмная сила (СПС), представляющая собой сумму аэродинамической и трастовой подъемных сил (АПС и ТПС), превосходит вес этого объекта. В мировой авиации наработан опыт взлета и посадки летательных аппаратов (ЛА), условно разделяющий множество вариантов взлета на три категории: обычный взлет с нефорсированным разбегом (Conventional Take-Off and Landing (CTOL)), форсированный взлет с коротким разбегом (Short Take-Off and Landing (STOL)), вертикальный взлет (Vertical Take-Off and Landing (VTOL))
, . В основе взлета CTOL находится АПС крыльев и фюзеляжа (для вертолета – еще и вертикальная ТПС винта) – возникающая и растущая со скоростью разбега ЛА. Для реализации STOL к АПС, как правило, подключаются силы вспомогательных средства создания дополнительной вертикальной тяги с выполнением специального сценария разгона и отрыва от ОП. Реализация взлета VTOL до достижения режима полного висения ЛА производится почти без участия АПС – за счет ТПС одного или нескольких трастеров (если не считать граунд-эффект близости земли , , , у вертолетов и экранопланов , а также некоторое сопротивление воздуха вертикальному движению ЛА).Как видим, универсальной схемы, алгоритма взлета существующих ЛА нет. В связи с этим возникает гипотеза: С внедрением в конструкцию ТС КДД моделирование взлета экипажа станет возможным по единому алгоритму, охватывающему все способы (варианты) взлета: CTOL, STOL и VTOL.
Кроме верификации этой гипотезы предстоит также оценить динамику процессов в совокупности вариантов взлета квантомобилей. Здесь учет упругих сил и демпфирования в подвеске экипажа является, несомненно, важным. При этом, в дополнение к каноническому моделированию колебательного процесса подвески автомобиля, требует рассмотрения и моделирования не столь изученный процесс отрыва колес от ОП; втягивание подвески в корпус из-под днища с выдвижением оперения; связанное с этим изменение конфигурации экипажа и др. Сконцентрировав внимание на этом технологическом аспекте и допустив, что колебание неподрессоренных масс у квантомобиля оказывает незначительное влияние на перемещение подрессоренных масс, колебательную систему подвески представим в МПДК в самом упрощенном виде: одномассовая колебательная система под нагрузкой с одной приведенной жесткостью (упругостью) cup подвески в целом и одним общим приведенным коэффициентом демпфирования амортизаторов kam, приложенным к общей массе экипажа m , .
2. Методы и принципы исследования
2.1. Цель и задачи исследования
Целью расчетного исследования явилось формирование модели взлета квантомобиля с обеспечением возможности количественной оценки динамики сопутствующих процессов.
Отсутствие признанных теоретических основ движения квантомобиля, натурных образцов исследуемых объектов и эмпирических данных по ним, вызывает необходимость использовать подход с опорой на программное имитационное моделирование (ПИМ).
Задачами по достижению цели являются:
1) формирование математической модели движения квантомобиля под поставленную цель;
2) разработка в авторской Simulink-модели приземного движения квантомобиля (МПДК) Подсистемы взлета и вывешенного движения (ПВВД) с реализацией последовательности этапов движения: I – лифт экипажа до высоты отрыва колес от ОП Hlf1; II – лифт до высоты убирания подвески и выпуска оперения Hlf2; III – лифт до нижней высоты безопасности полета Hlf3;
3) отработка интерфейса взаимодействия с моделью, задания сценариев взлета, контроль движения экипажа, многофакторного вывода результатов;
4) проведение ПИМ на базе Simulink-модели с экспериментами, охватывающими некоторое множество вариантов взлета ТС;
5) обсуждение и обобщение результатов расчетов;
6) формирование рекомендаций и выводов.
2.2. Идейная основа модели движения квантомобиля с учетом вывешивания
Исследование влияния прикладываемых к экипажу в плоскости тангажа горизонтальных и вертикальных сил на продольную устойчивость ТС в рамках 3-DOF моделирования (3 degrees of freedom
) автором осуществлялось в работах , , . В настоящем исследовании, однако, поскольку намерены исследовать в плоскости тангажа лишь траектории взлета, с отводом вопроса обеспечения продольной устойчивости ТС, достаточно модели с двумя степенями свободы (2DOF ). Это позволяет условно совместить в исследовании центр тяжести (ЦТ), центр давления (ЦД) и точку приложения траста (ТПТ) КД в срединной плоскости базы ТС. При этом будем помнить, что при учете реальных локаций ЦТ, ЦД и ТПТ траектории взлета будут отличаться от анонсируемых настоящим исследованием (из-за дополнительных энергозатрат на поддержание устойчивости экипажа).Взлет (в плоскости тангажа) представляется двумя компонентами движения: горизонтальной и вертикальной. Горизонтальная составляющая МПДК представлена в авторских работах
, , , ; здесь, однако, для целостного восприятия взаимодействия таковой с вертикальной компонентой ее кратко представим. Вертикальную же компоненту движения при взлете изложим изначально.Баланс горизонтальных сил, действующих на квантомобиль
, :где Fr – сила сопротивления качению опорных колес, Н;
Fwx – сила сопротивления воздуха продольному движению, Н;
Fax – продольная сила инерции экипажа, Н;
Gq' – сила давления экипажа на ОП с учетом частичного лифта, Н;
fk0 – коэффициент сопротивления качению колес при нулевой скорости;
fkv – скоростной коэффициент сопротивления качению колес, с2/м2;
Vq – скорость продольного движения квантомобиля, м/с;
cd – коэффициент продольного аэродинамического сопротивления;
ρw – плотность воздуха, Н ×с2/м4;
Sfr – фронтальная (лобовая) площадь экипажа, м2;
Gq – сила тяжести квантомобиля, Н;
g – ускорение свободного падения, м/с2;
ax – продольное ускорение экипажа, м/с2;
δwh – коэффициент инерции вращения опорных колес экипажа.
Сила Gq' = Gq – (FTz+Fwz) = Gq – FzSum, где FzSum – суть СПС. Для квантомобиля приведенная масса m’ = Gq(1+δwh)/g учитывает вращение только опорных колес (привод отсутствует).
Сформируем баланс вертикальных сил, действующих на квантомобиль.
Система вертикальных перемещений экипажа на этапе I с опорой на колеса в упрощенном виде (конфигурация 1): одномассовая система с одной степенью свободы, с учетом вертикальных сил сопротивления подвески, при этом с приведенными коэффициентами жесткости (упругости) подвески и демпфирования, без учета воздействия профиля ОП (ровное полотно, характеризуемое двумя коэффициентами: fk0 и fkv). Динамическая модель ТС охватывает также этап II движения вывешенного над ОП экипажа с висящей подвеской (все еще конфигурация 1), за ним этап III – с убранной подвеской и выдвинутым оперением (конфигурация 2).
Для исходного положения статического равновесия, когда СПС FzSum= 0 и на экипаж снизу действует лишь сила упругости Fup= Gq =m*g, примем z = 0.
При наличии силы 0 < FzSum < Gq (опять же для статики, но при промежуточном положении подвески z > 0) можно записать:
Gq = FzSum+Fup, т.е. сила упругости убывает на величину возникающей СПС FzSum.
При z = Gq /cup=Hlf1 (в момент, когда подвеска высвобождается и колеса отрываются от ОП) сила FzSum полностью замещает силу упругости Fup (в противодействии все той же силе тяжести Gq = const).
В динамике добавляются силы, зависящие от вертикальной скорости квантомобиля vz: сила сопротивления амортизаторов Fam = f(vz) и сила сопротивления воздуха вертикальному перемещению экипажа Fvpl = f(vz2); а также – инерционная сила, зависящая от вертикального ускорения az: Faz = f(az). Баланс сил теперь выглядит так:
С учетом того, что Fup(z) = Gq – z*cup, можно записать:
Обозначив z*cup = Fpz и заметив, что это – высвободившаяся часть силы упругости, перешедшая в потенциал лифта, можем записать для силы, остающейся на ускорение экипажа:
где Fvz = Fvpl(vz2) + Fам(vz) – совокупность сил, связанных со скоростью вертикального движения экипажа.
В форме ДУ это:
где: kam – приведенный коэффициент демпфирования амортизаторов подвески, Н*с/м;
kwv = cdv *(ρw/2)*Spl – фактор вертикальной обтекаемости экипажа, Нс2м-2;
cdv – аэродинамический коэффициент сопротивления вертикальному перемещению экипажа;
Spl – площадь в плане экипажа, м2.
При наличии двух (или более) конфигураций экипажа величѝны cdv и Spl будем индексировать, например, для исходной конфигурации 1 (для высот 0 ≤ z ≤ Hlf2) – cdv1 и Spl1, а для лётной конфигурации с высотой z > Hlf2 – cdv2 и Spl2.
В момент перехода с этапа I к этапу II сила Fpz = Gq – сила тяжести так и присутствует далее на взлете и в полете. Однако для амортизатора картина иная: происходит ступенчатый сброс силы сопротивления с некоего уровня до нуля. Пробные расчеты в МПДК показали возможность ударных импульсов при ступенчатом сбросе (физически при отсутствии специальных устройств) до нескольких десятков g.
Для устранения этого в МПДК внедрен Модуль формирования снижения сопротивления амортизатора вблизи конечной точки хода штока – посредством реализации Экспоненциального сигмоида
:При достижении значения pz = Gq/cup рессоры переходят в свободное состояние (вывешиваются, с отрывом колес от ОП). Поддерживающая сила Fpz = Gq. Этап I (с достижением высоты Hlf1) заканчивается.
Начинается этап II – подъем экипажа с висящей подвеской до высоты Hlf2 (например до 10 м). Здесь kam = 0, cup = 0, cdv = cdv1, Spl = Spl1.
На высоте Hlf2 начинается этап III. В его начале подвеска вбирается в корпус экипажа, одновременно выдвигается оперение: cdv = cdv2, Spl = Spl2. Подъем продолжается до высоты Hlf3 (например, до 25 м). Взлет заканчивается с фиксацией результатов.
Симуляция взлета и продолжения полета может быть продолжена при задействовании переключателя режима работы программы.
2.3. Программное обеспечение модели МПДК
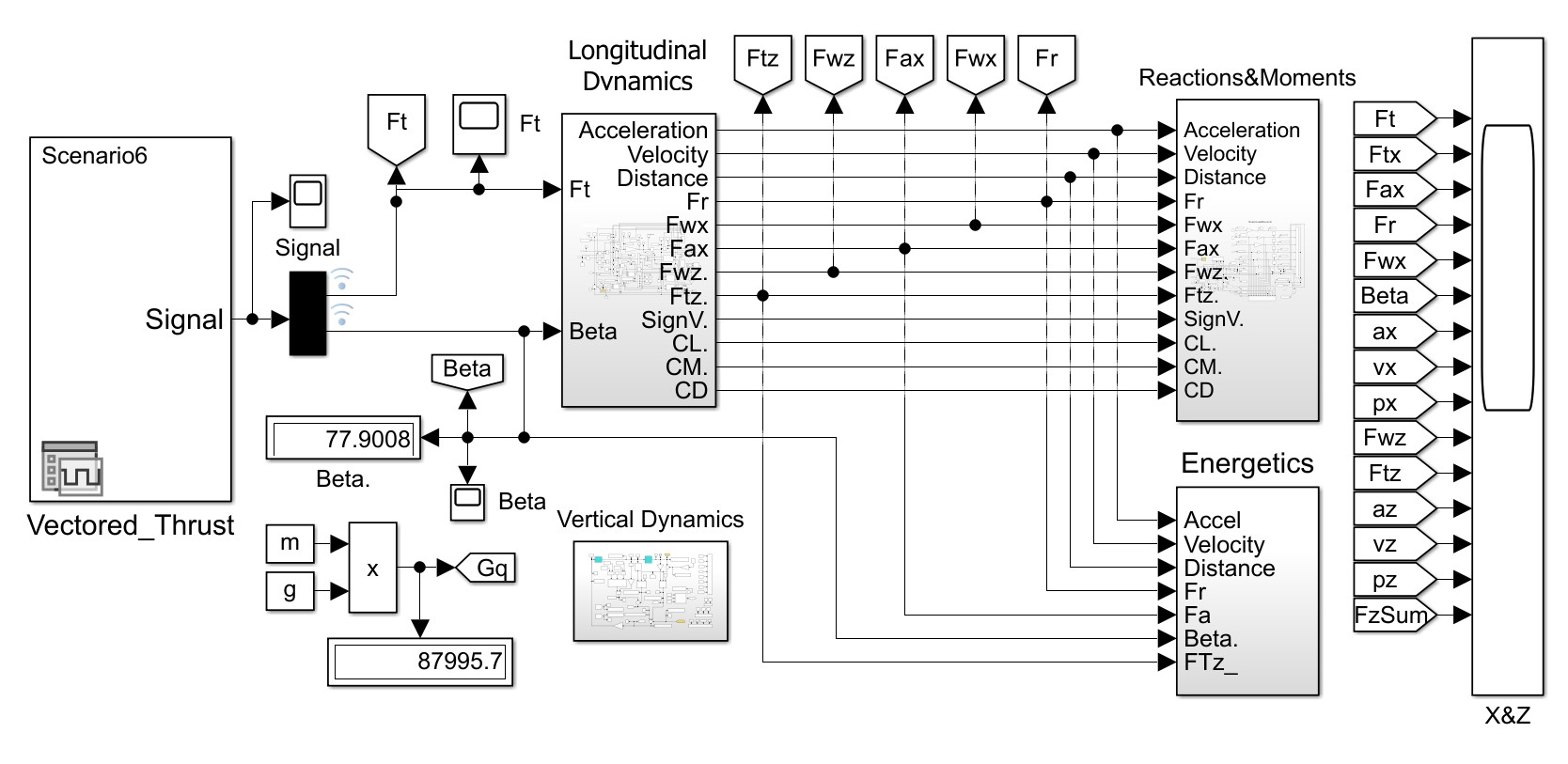
Рисунок 1 - Главный модуль S-модели МПДК
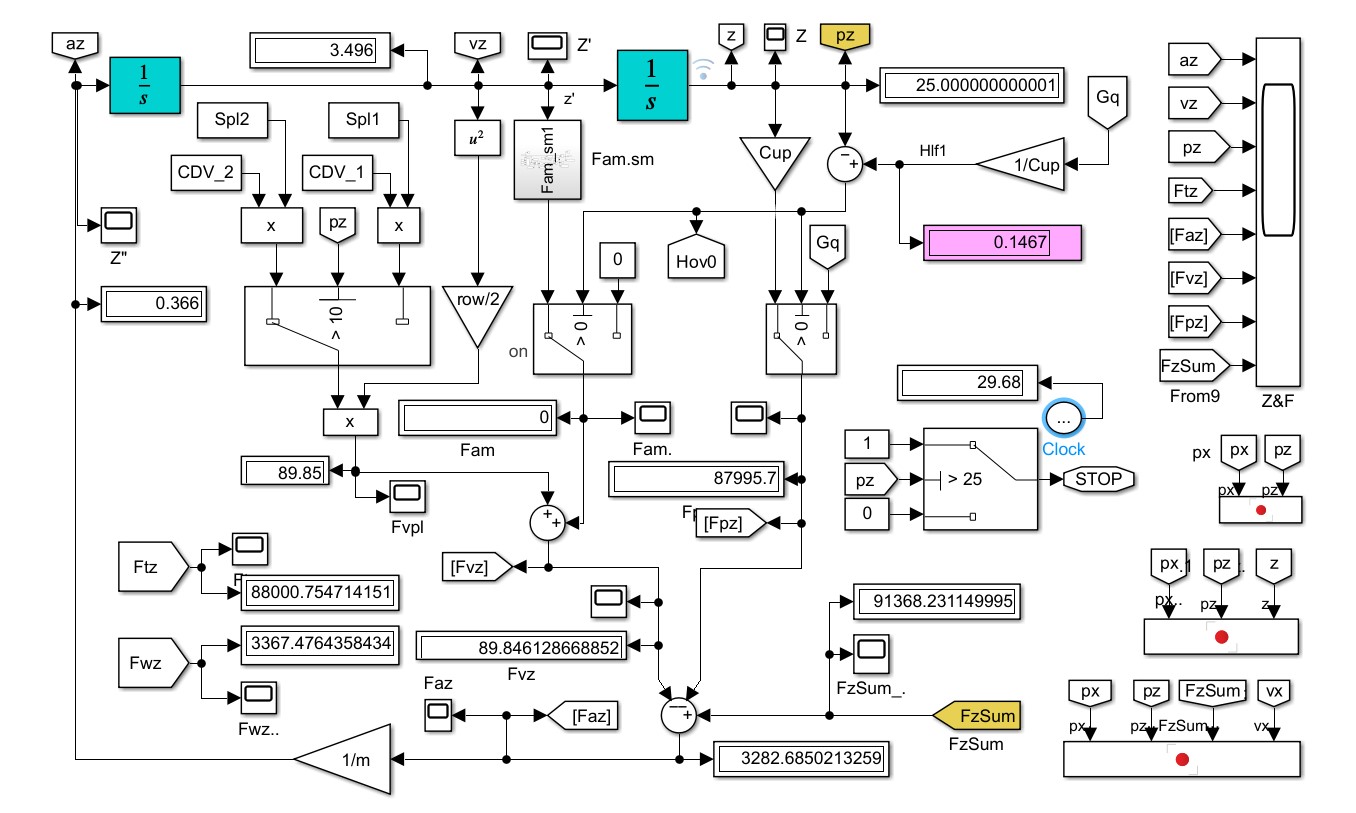
Рисунок 2 - Модуль вертикальной динамики квантомобиля Vertical Dynamics
Вверху на схеме рис. 2 действуют два интегратора (1/s), формирующие вертикальные скорость vz и позицию pz экипажа. Подсистема содержит блок остановки по достижении заказанного положения pz с фиксацией модельного времени (блок Clock). На рис. 2 виден замаскированный блок Fam.sm формирования сигмоидального сглаживания по формуле (9).
Имеется множество дисплеев и осциллографов для отслеживания значений показателей на временнóй шкале. Имеется также три блока Record (см. юго-восточный угол схемы) – для отображения показателей в зависимости от пространственного положения экипажа.
3. Результаты расчета показателей движения квантомобиля
3.1. Подготовка моделей квантомобилей
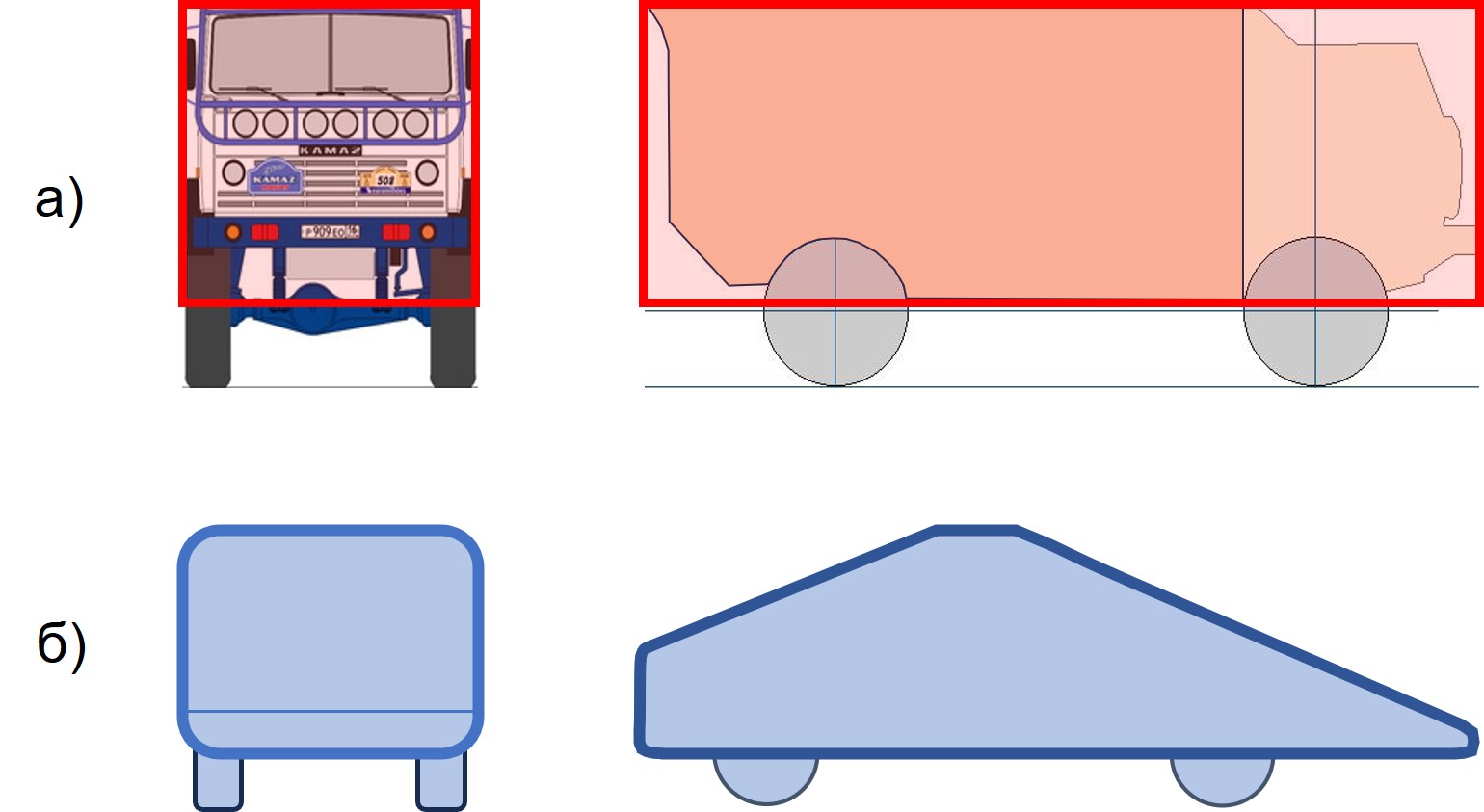
Рисунок 3 - Профили моделей ПОТ:
а - 1-Box; б - Davis
Таблица 1 - Основные данные по моделям 1-Box и Davis
Параметр | 1 | 2 |
1-Box | Davis | |
L, м | 7,3 | 7,3 |
W, м | 2,55 | 2,55 |
H, м | 3,3 | 1,87 |
Sfr1, м2 | 8,5 | 4,76 |
Sfr2, м2 | 7,5 | 5,5 |
Lwb, м | 4,25 | 4,87 |
L2, м | 2,125 | 2,435 |
Hg, м | 1,3 | 0,9 |
Hw, м | 1,46 | 1,0 |
rd, м | 0,5 | 0,5 |
m, кг | 8970 | 8970 |
Gq, Н | 87995,7 | 87995,7 |
FT, Н | 90000 | 90000 |
cd1 | 0,32 | 0,263 |
cd2 | 0,3 | 0,25 |
cl1 | 0 | 0,42 |
cl2 | 0,1 | 0,35 |
cm1 | 0 | –0,35 |
cm2 | 0,1 | –0,2 |
cdv1 | 0,8 | 0,6 |
cdv2 | 0,7 | 0,5 |
Spl1, м2 | 18 | 15 |
Spl2, м2 | 24 | 24 |
fk0 | 0,3 | 0,02 |
fkv, с2/м2 | 0,00037 | 0,00037 |
ЦТ обеих моделей расположили в их срединных плоскостях колесной базы (L2=Lwb/2, где Lwb – колесная база, а L2 – расстояние от ЦТ до вертикальной плоскости задней оси). Точку приложения траста расположили в ЦТ.
В целях возможности продольного движения экипажа весом 88 кН при его полном вывешивании выбрали траст FT = 90 кН (обосновано в
, ). Во всех расчетных реализациях взлета рост траста с нуля до 90 кН происходит за 5 секунд.3.2. Вертикальный лифт
Сначала рассмотрели только лифт до высоты Hlf3 = 25 м с приложением к ПОТ вертикально направленного траста, без горизонтального движения экипажа (FT = 90 кН, β=90°).
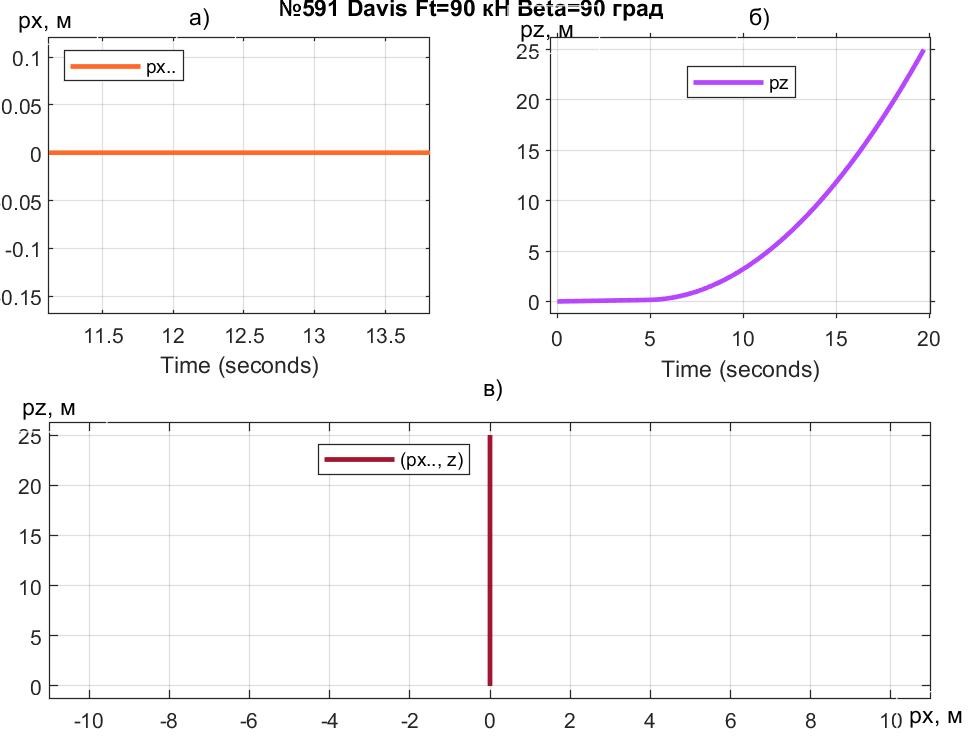
Рисунок 4 - Перемещение модели Davis под воздействием траста FT = 90 кН и β = 90°
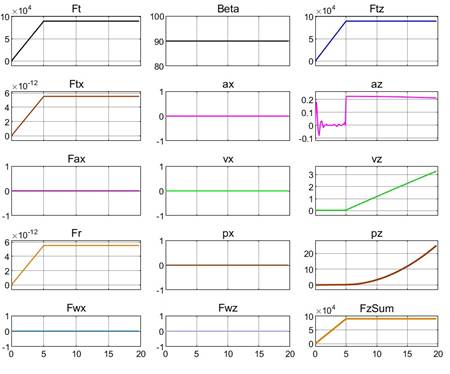
Рисунок 5 - Совокупность показателей процесса вертикального лифта ПОТ 1-Box до высоты Hlf3=25 м
Примечание: FT = 90 кН, β = 90°
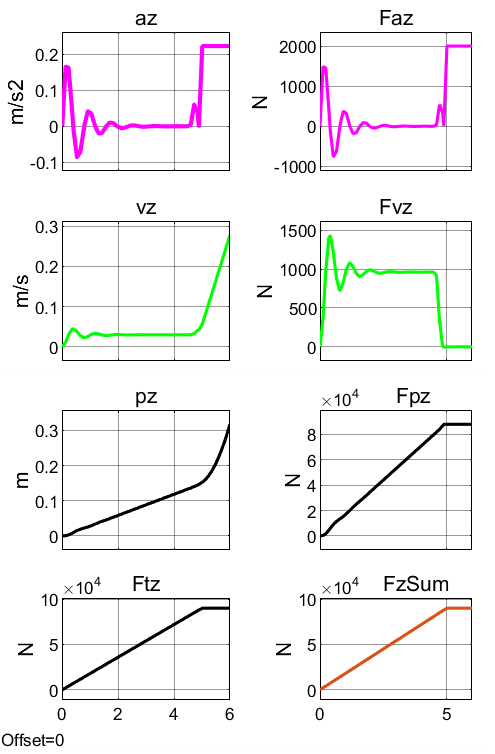
Рисунок 6 - Процессы изменения показателей вертикального движения квантомобилей в первые 6 секунд лифта
Примечание: и 1-Box, и Davis
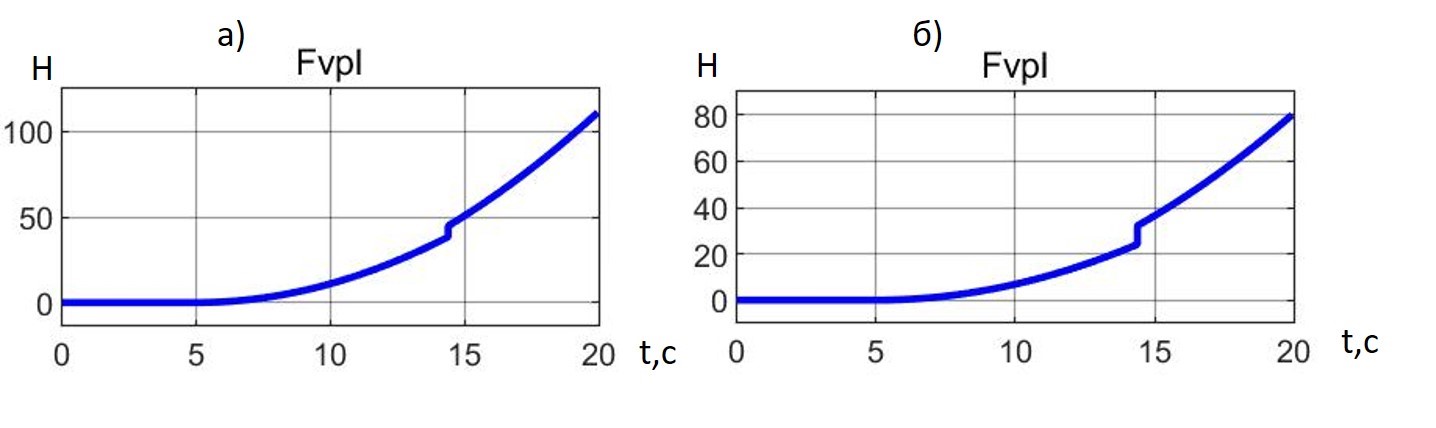
Рисунок 7 - Сила аэродинамического сопротивления вертикальному движению экипажа Fvpl:
а - 1-Box; б - Davis
Траст FT = 90 кН, в отсутствие АПС, может обеспечить вывешивание экипажа весом Gq = 88 кН с отрывом колес от ОП в пределах изменения угла β = 90 ÷ 77,9°, когда FTz ≥ Gq.
Далее для обеих машин рассмотрели их движение при угле наклона траста β = 77,9°. При угле β = 77,9° FTx = 18,87 кН. Тяговая сила FTx, идущая в этом случае только на преодоление сопротивления воздуха и сил инерции, позволяет разогнать экипаж в вывешенном состоянии до существенной скорости
.Вместе с тем при начальном росте величины FT (и одновременно FTx) приходится преодолевать меняющуюся силу сопротивления качению колес Fr, да еще с учетом сопротивления страгивания колес (см.
).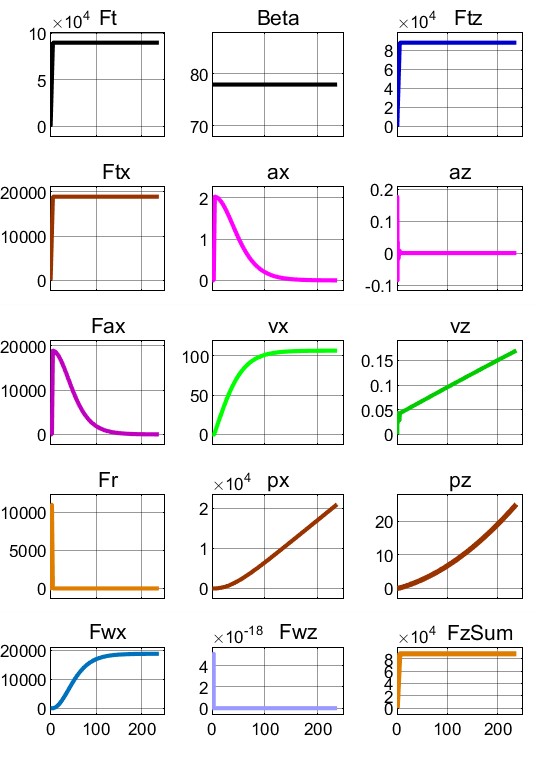
Рисунок 8 - Показатели лифта 1-Box до pz = 25 при β = 77,9° во времени t
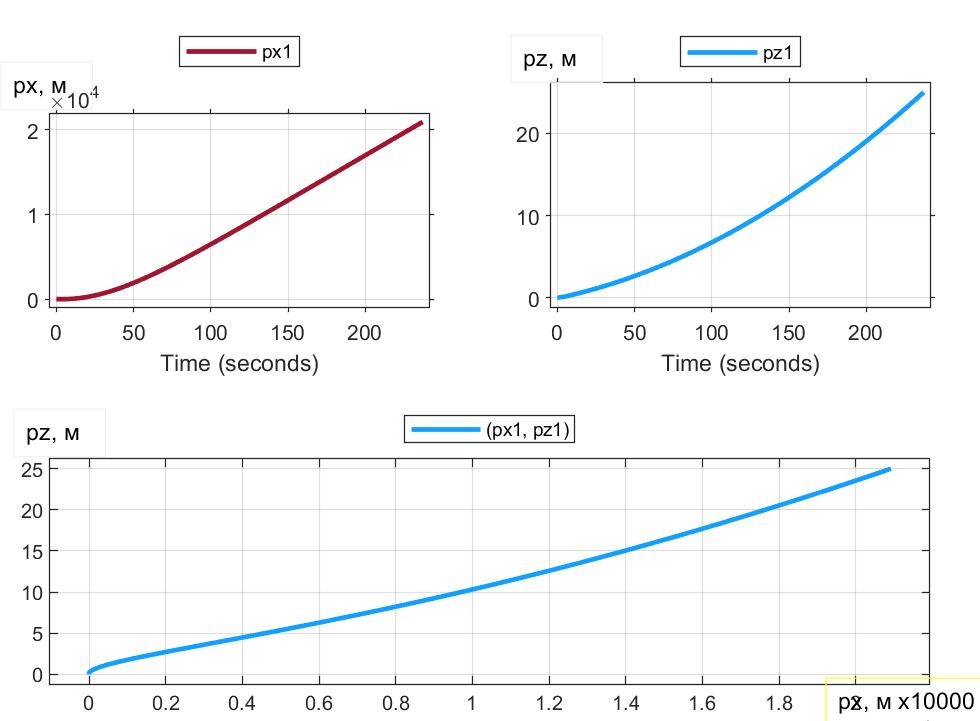
Рисунок 9 - Перемещение ПОТ 1-Box под воздействием траста FT = 90 кН и β = 77,9°
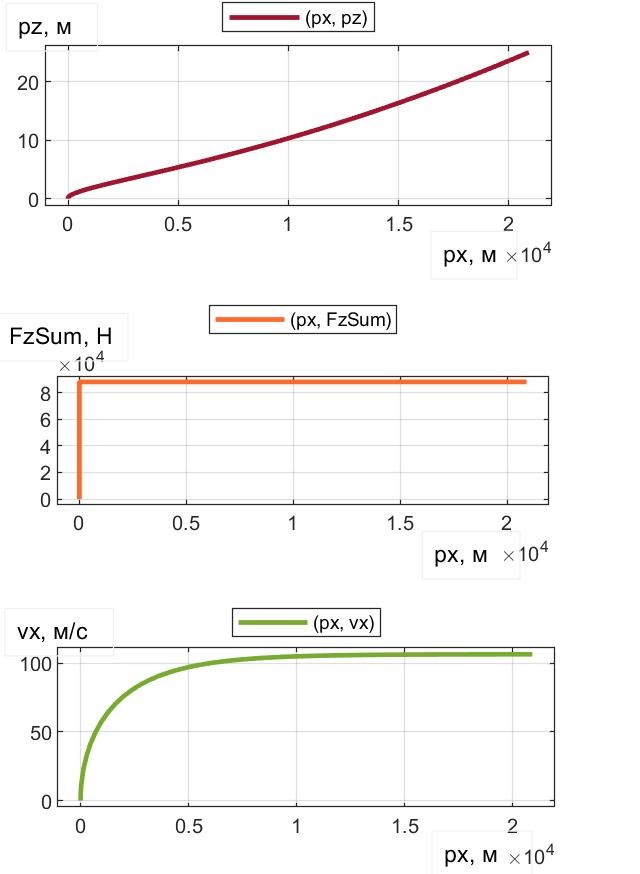
Рисунок 10 - Зависимость лифта, СПС и продольной скорости ПОТ 1-Box от пути при FT = 90 кН и β = 77,9°
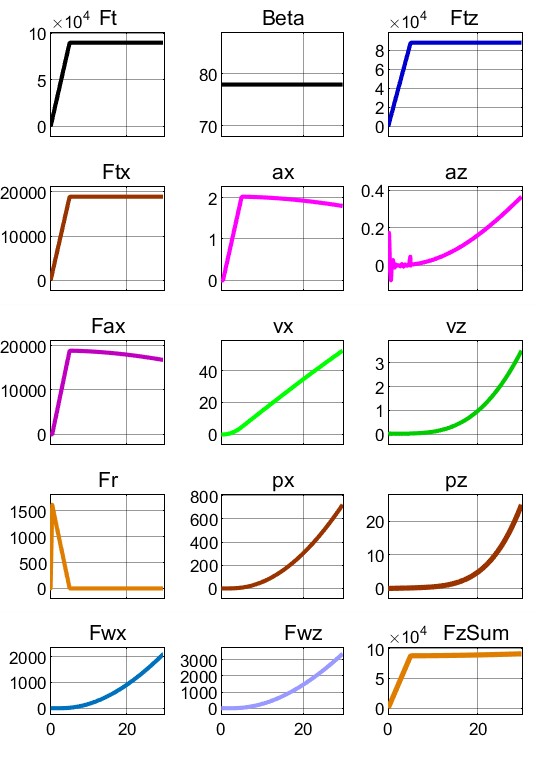
Рисунок 11 - Показатели лифта ПОТ Davis до pz = 25 м при β = 77,9° во времени t
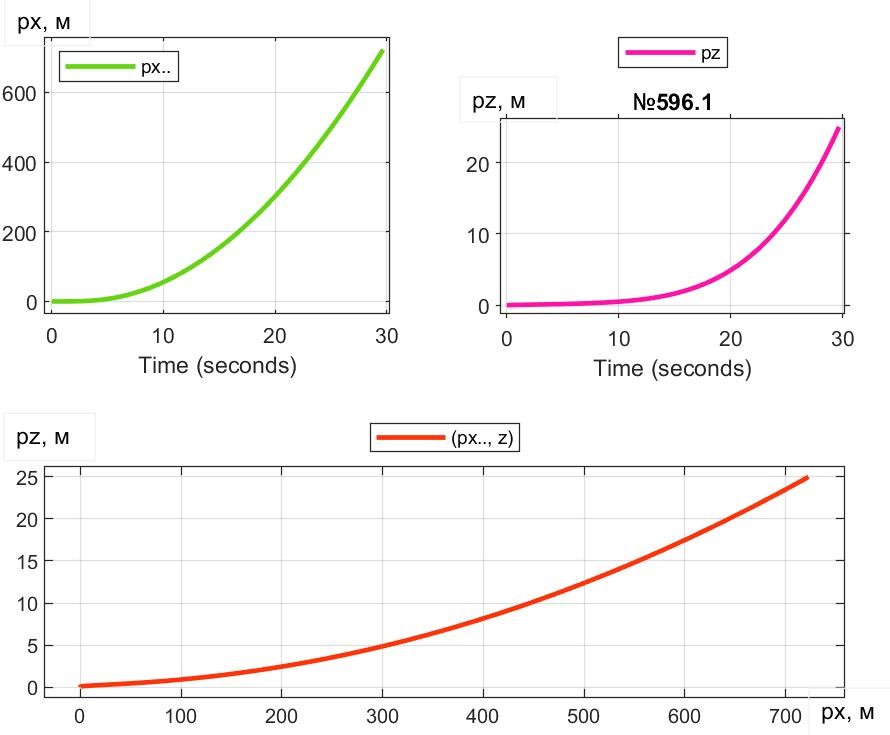
Рисунок 12 - Перемещение ПОТ Davis под воздействием траста FT = 90 кН и β = 77,9°
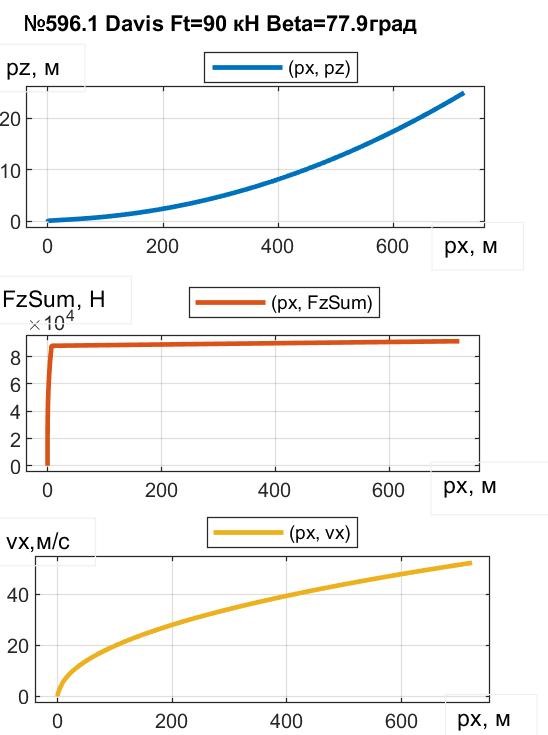
Рисунок 13 - Зависимость лифта, СПС и продольной скорости ПОТ Davis от пути при FT = 90 кН и β = 77,9°
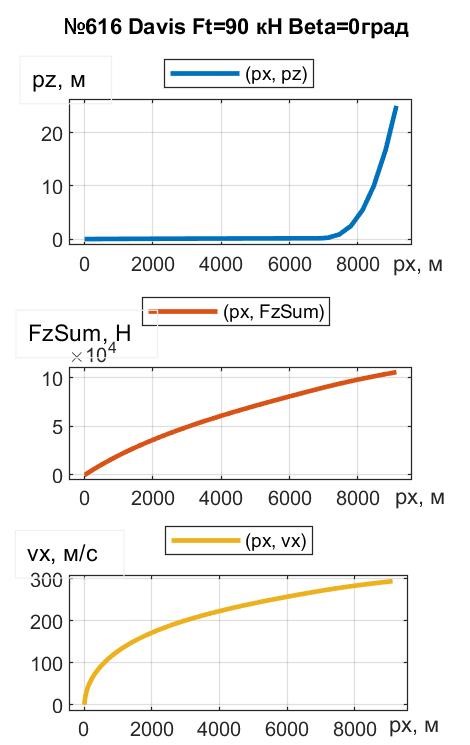
Рисунок 14 - Зависимость лифта, СПС и продольной скорости ПОТ Davis от пути при FT = 90 кН и β = 0°
В МПДК один из вариантов подсистемы формирования заданий Vectored_Thrust (см. рис. 1) позволяет реализовать с одного запуска множество заданий расчета с перебираемыми значениями исходных параметров, с получением обобщающего графика.
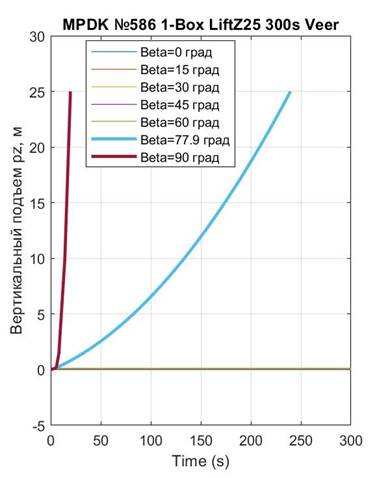
Рисунок 15 - Реализация лифта во времени до высоты Hlf3 = 25 м у ПОТ 1-Box
Примечание: вариации β = 0°, 15°, 30°, 45°, 60° графически неотличимы
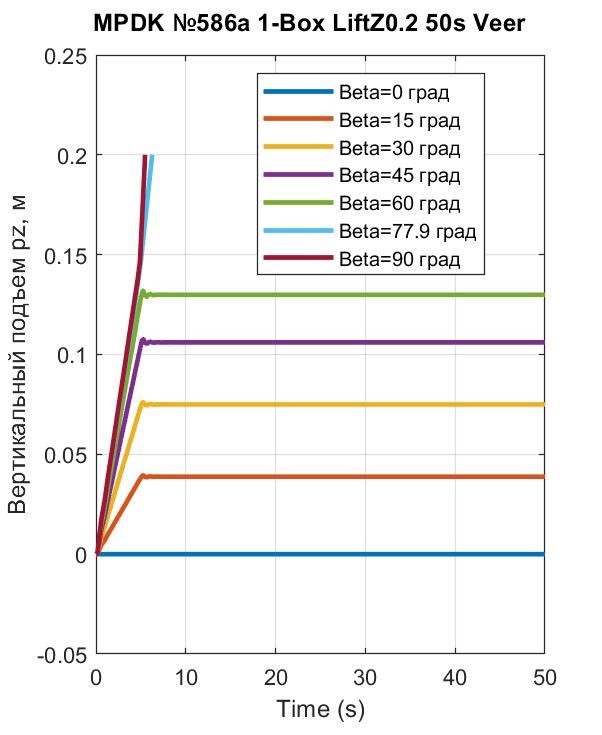
Рисунок 16 - Начальные эпизоды развития лифта во времени до высоты pz = 0,2 м у ПОТ 1-Box
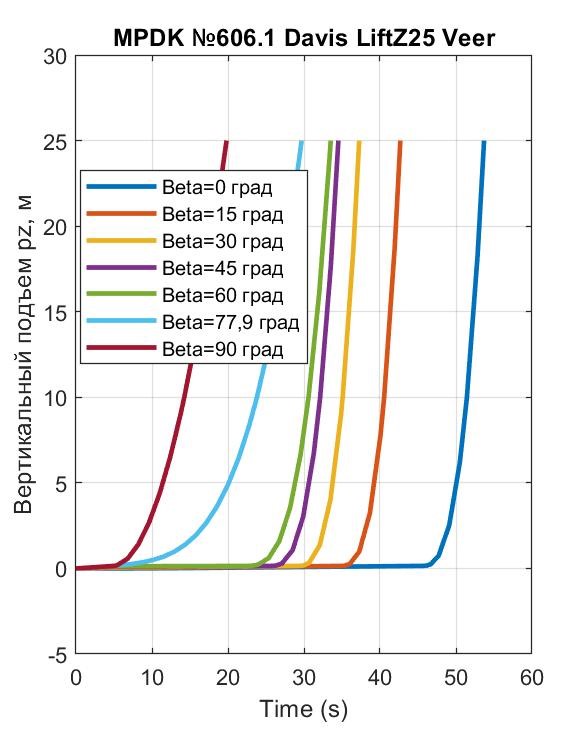
Рисунок 17 - Реализация лифта во времени до высоты Hlf3 = 25 м у Davis
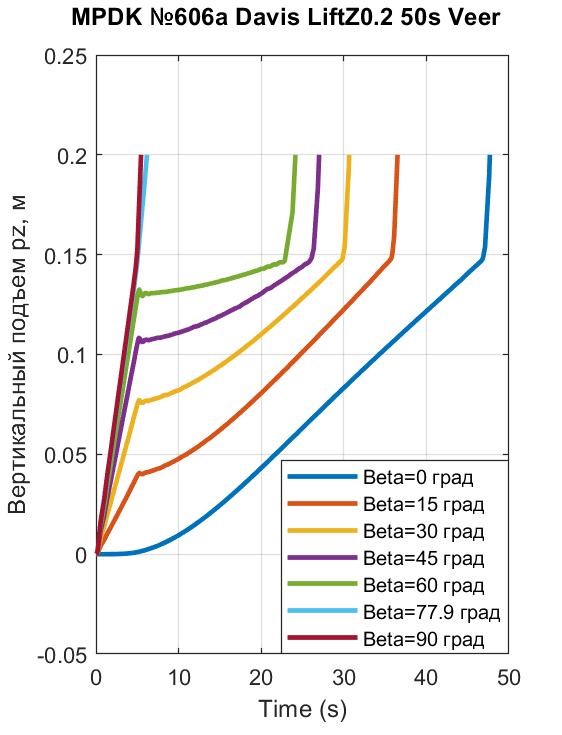
Рисунок 18 - Начальные эпизоды развития лифта во времени до высоты pz = 0,2 м у Davis
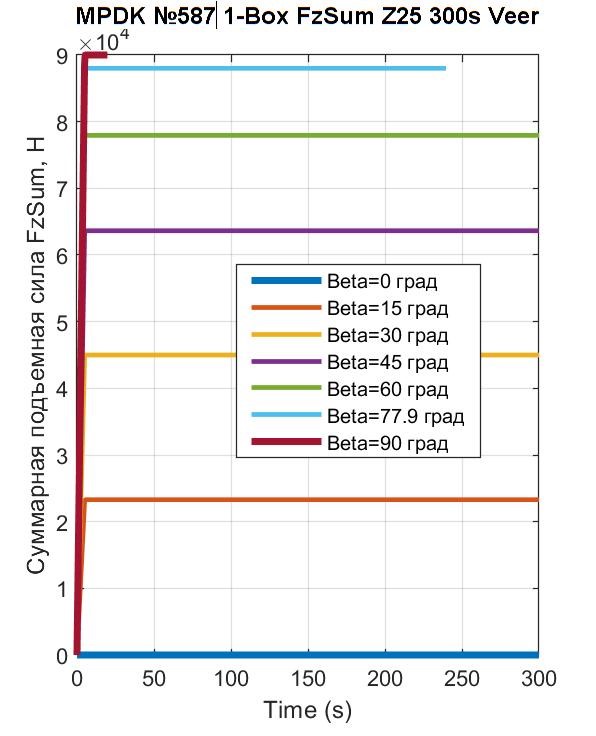
Рисунок 19 - СПС FzSum, генерирующая лифт 1-Box при различных наклонах траста
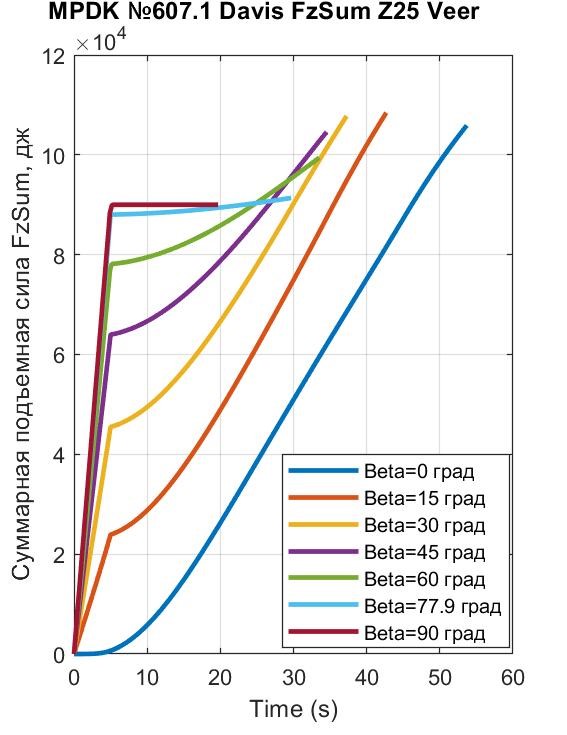
Рисунок 20 - СПС FzSum, генерирующая лифт Davis при различных наклонах траста β
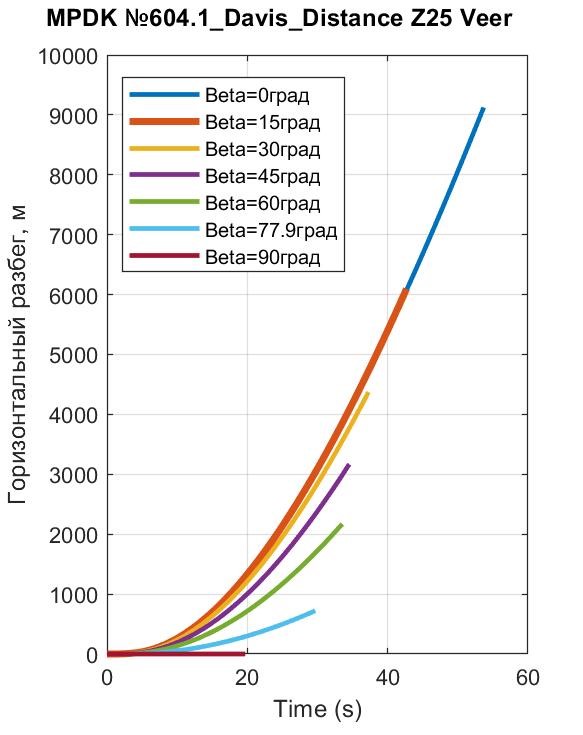
Рисунок 21 - Горизонтальные разбеги Davis до лифта pz = 25 м при различных углах наклона траста β
4. Обсуждение
4. Обсуждение результатов расчетов
Совокупность представленных расчетов нацелена, во-первых, на демонстрацию возможностей МПДК в части представления особенностей взлета квантомобиля, а во-вторых, – на построение каркаса опорных вариантов для последующей гибкой оптимизации взлетных стратегий в этой структуре.
Графики вида рис. 4, 9 и 12, давая плоскостное представление об изменении координат модели движения объекта, по сути являются проекциями траектории F(t,px,pz) на плоскости t-0-px, t-0-pz и px-0-pz и представляют возможную базу для перехода к анализу траекторий в трехмерном пространстве.
С количественной точки зрения выяснили, например, (см. рис. 9 и 12), что при β = 77,9° ПОТ 1-Box достигает высоты Hlf3=25 м на пути px = 20920 м за 237 с, тогда как Davis достигает Hlf3, пробегая путь px = 723 м за 29,7 с. Уяснить причины можно с помощью рис. 8 и 11. Видим, что сила сопротивления воздуха Fwx у 1-Box достигает 19000 Н, тогда как у Davis – лишь 2100 Н, что дает возможность в балансе горизонтальных сил Davis реализации намного превосходящей силы Fax (и соответственно – ускорения ax). В балансе вертикальных сил, наличие у Davis АПС Fwz (до 3500 Н) увеличивает на эту величину СПС FzSum, что приводит к повышенным az и vz, и как следствие, – к более быстрому достижению высоты Hlf3 = 25 м.
Полезно проследить по рис. 6 динамику движения экипажа в первые 6 секунд взлета. Видим, что при z = Hlf1 = 0,1467 м (Gq/cup = 88000Н / 600000Н/м = 0,1467 – см. на рис. 2 сиреневый блок), экипаж, под действием FTz, выросшего до 90 кН, и освободившись от силы сопротивления амортизаторов Fam, устремляется вверх с растущей скоростью vz. Также видим, что колебания от первичного силового импульса затухли за 3 периода, что свидетельствует об удовлетворительном сочетании характеристик упругих элементов и амортизаторов.
Упомянутое незначительное отличие процессов лифта двух экипажей проявляется только из-за разницы параметров аэродинамики вертикального движения: cdv и Spl. По рис. 7 видим, что разница – незначительная: по причине малых скоростей vz (не более 3,3 м/с по графику рис. 5). Но при этом, всё-таки, можно отметить более низкий уровень сопротивления Fvpl у более совершенного профиля Davis.
Ответ о развиваемых скоростях при взлете до высоты 25 м по времени vx(t) и vz(t) можно получить по графикам вида рис. 8 и 11, а по пути vx(x) и vz(x) – вида рис. 10 и 13. Числовые показатели взлета, соответствующие этим графикам, снесены в табл. 2.
Таблица 2 - Показатели взлета ПОТ при β = 77,9°
ПОТ | t, с | px, м | vx, м/с | pz, м | vz, м/с |
Davis | 29,7 | 723 | 52 | 25 | 3,5 |
1-Box | 237 | 20920 | 106,4 | 25 | 0,17 |
1-Box | 29,7 | 684 | 49,5 | 1,4 | 0,056 |
Анализируя показатели двух верхних строк, можно, например, отметить, что целевое событие достижения высоты лифта Hlf3 = 25 м происходит при t = 29,7 c и 237 c, но при px = 723 м и 20920 м, при этом максимальные скорости: 52 м/с и 106,4 м/с (для 1-Box и Davis, соответственно). В последней строке помещены показатели 1-Box, полученные для целевого события t = 29,7 c. Видим, что за время, когда Davis поднимается на 25 м, 1-Box – всего на 1,4 м. Ни px = 20920 м, ни pz = 1,4 м – явно неприемлемы: и это требует для улучшения показателей привлечения комбинирования величиной и углами траста c использованием оптимизационных методов.
Анализ графиков на рис. 15 показывает, что взлет ПОТ 1-Box до высот Hlf2 и Hlf3 при FT = 90кН и углах β < 77,9° невозможен. Высóты, до которых приподнимается ПОТ 1-Box под воздействием названого траста и углов β < 77,9°, отражены на рис. 16 – все они в пределах Hlf1 = 0÷0,1467 м работы подвески.
Картина существенно меняется при генерации АПС у Davis. Временные графики взлета этого ПОТ до высоты Hlf3 = 25 м приведены на рис. 17. Детализация характера перемещений в пределах работы подвески отражена на рис. 18. Сравнивая графики рис. 16 и рис. 18, видим, что в первые 5 секунд лифт обоих экипажей практически одинаков (подвески одинаковы, ТПС – одинаковы, АПС у Davis при малой скорости vx ничтожна). Далее (привлекая рис. 15 и рис. 17) выявляем существенную разницу в реализации вывешивания экипажей, обусловленную разницей сопротивления ОП и воздуха.
Анализ расчетных материалов по всем углам наклона траста β при взлете ПОТ Davis позволил сформировать сводную таблицу 3.
Таблица 3 - Сводная таблица показателей расчетов по взлету ПОТ Davis до высоты 25 м со сменой угла наклона траста β
№ пп | β, град | t, c | px, м | vx, м/c | vz, м/c | FTz, кН | Fwz, кН | FzSum, кН |
1 | 0 | 53,7 | 9126 | 294 | 8,65 | 0 | 106 | 106 |
2 | 15 | 42,7 | 6095 | 264 | 9,21 | 23 | 85 | 108 |
3 | 30 | 37,3 | 4375 | 226 | 9,03 | 45 | 63 | 108 |
4 | 45 | 34.5 | 3169 | 183 | 8,23 | 64 | 41 | 105 |
5 | 60 | 33,5 | 2171 | 132 | 6,79 | 78 | 21 | 99 |
6 | 77,9 | 29,7 | 723 | 52 | 3,50 | 88 | 3 | 91 |
7 | 90 | 19,9 | 0 | 0 | 3,3 | 90 | 0 | 90 |
8 | 90→64,75 | 29,7 | 195 | 36 | -3, 1 | 81 | 2 | 83 |
Анализ данных строк 1…7 табл. 3 позволяет отметить следующее. Минимальным временем подъема до высоты 25 м (19,9 с) отличается вертикальный лифт (β = 90°). Длительность лифта при наклоне траста β = 77,9° – больше на 50% (29,7 с).
Наибольшей длительностью, естественно, характеризуется лифт при горизонтальном трасте (β = 0°, t = 53,7 с) – здесь при ТПС FTz = 0 проявляется задержка с накоплением достаточной для вывешивания АПС. Отметим, что, во-первых, разбег взлета px = 9126 м – практически неприемлем, а во-вторых, результаты строк с 5-той по 1-ю – малоубедительны, поскольку принятые значения коэффициентов cd и cl для ПОТ Davis действенны до скоростей vx ≈ 50 м/с
, . Показатели строк 1…5 носят сослагательный характер, свидетельствующий о возможности расчетов при наличии достоверной информации о высоких скоростях.Взяв за основу лифт с «однонаклонным» трастом β = 77,9°, имеет смысл сравнить его с комбинацией углов наклона β в процессе вывешивания экипажа. Примером может быть траектория лифта с углом β = 90° до t =19,9 с (см. вариант 7 табл. 3), затем движение до t = 29,7 c (в соответствии с длительностью варианта 6 табл. 3 и подобранным β = 64,75°). То есть при равенстве продолжительности движения (29,7 с) – оценить разбеги экипажа. Результаты помещены в строке 8 табл. 3. Они вынесены также на рис. 22 – для сравнения с рис. 4 и рис 12. Видим, что «комбинированный» вариант (px = 195 м) намного уступает «однонаклонному» варианту (px = 723 м), во всяком случае, для данного примера.
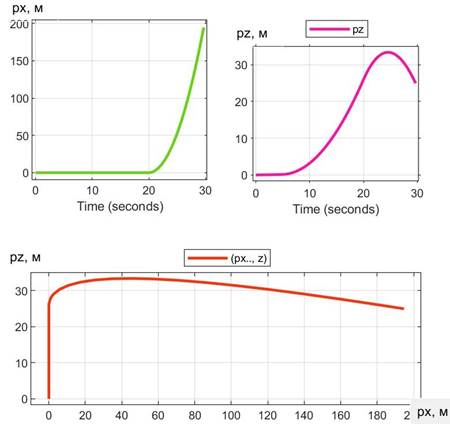
Рисунок 22 - Перемещение ПОТ Davis под воздействием траста FT = 90кН и β = 90° →64,75°
Примечание: строка 8 в табл. 3
Для ПОТ Davis (см. рис. 17 и 18) взлет возможен любым способом (VTOL, STOL, либо CTOL), поскольку достаточная для вывешивания АПС возникает при какой-либо скорости vx. Например, даже при β = 0° (FTz = 0), благодаря тому, что СПС FzSum при t ≈ 47 c достигает значения Gq = 88кН (экипаж при pz = Hlf1 отрывается от ОП – см. рис. 18 и 20), а при t ≈ 53,7 c экипаж достигает назначенной высоты Hlf3 = 25 м (см. рис. 17), – условный взлет реализуется.
Можно утверждать, что при любой достоверности данных табл. 3 важным является то, что поле способов CTOL, STOL и VTOL охватывается системой МПДК непрерывным образом, что подтверждается топологией семейств кривых на рис. 17 и 21. Рассмотренную же совокупность реализаций ПИМ можно рассматривать как некий каркас опорных траекторий взлета, в пределах которого находятся оптимальные.
5. Заключение
Разработанная в среде авторской Simulink-модели приземного движения квантомобиля (МПДК) подсистема взлета и вывешенного движения (ПВВД) Vertical Dynamics позволяет проводить расчетное исследование движения ТС в плоскости тангажа. Эта модель, по мнению автора, должна стать, во-первых, базой для оптимизационных расчетов взлета квантомобиля во многообразии его конфигураций и условий движения по ОП и рельефу местности, а во-вторых, – составной частью алгоритмов расчета динамических и траекторных показателей произвольного движения квантомобиля.
На базе проведенных посредством МПДК с ПВДД расчетов и их анализа преодолена познавательная сложность формирования траекторий движения квантомобиля на стадии его взлета во взаимосвязи трастовой и аэродинамической подъемных сил (ТПС и АПС).
Представленное исследование позволило утвердиться в гипотезе: С внедрением в конструкцию ТС КДД моделирование взлета экипажа станет возможным по единому алгоритму, охватывающему непрерывным образом все способы (варианты) взлета: CTOL, STOL и VTOL. Объединяющим фактором синтеза способов взлета является наличие у квантомобиля ТПС.
Дальнейшие исследования должны быть направлены на рассмотрение возможности применения развиваемого подхода к оптимизации траекторий движения квантомобилей, возможно, главным образом, беспилотных. Для этого понадобится, в первую очередь, привлечение комбинирования величинами и углами траста c использованием оптимизационных методов.
