ON MODELLING OF PERIODIC SURFACE WAVES OF AN IDEAL HEAVY INCOMPRESSIBLE FLUID

Моделирование периодических поверхностных волн идеальной тяжелой несжимаемой жидкости, которыми могут быть морские волны на глубокой воде, представляет трудность, так как нужно обеспечить одновременное удовлетворение нескольких условий. А именно, процесс должен быть периодическим, должны удовлетворяться уравнение Эйлера, являющееся следствием законов классической механики, и уравнение непрерывности, которое соответствует равенству притока и оттока несжимаемой жидкости в каждый момент времени для каждой элементарной области потока. Большинство известных моделей основано на постулировании предположений, например, что движение частицы жидкости является комбинацией кругового движения и поступательного, или о том, что поток является потенциальным, то есть, скорость в точках потока равна производной некоторой функции

На сегодняшний день не вызывает сомнений существование гигантских волн «встроенных» в поток периодических «обычной» амплитуды. Их моделирование является предметом отдельного исследования, необходимого для определения норм расчета судов и морских конструкций, а также для навигации, так как предположительно эти аномальные волны являются основной причиной морских катастроф

Для элемента единичного объема идеальной несжимаемой жидкости плотности ρ (или, что то же самое, элемента идеальной несжимаемой жидкости массы ρ) ламинарного потока справедливо равенство

(1)

где – вектор скорости элемента единичного объема жидкости плотности ρ, – время, – градиент давления .

При действии силы тяжести возникает дополнительное слагаемое , модуль вектора – ускорение свободного падения , то есть :

(2)

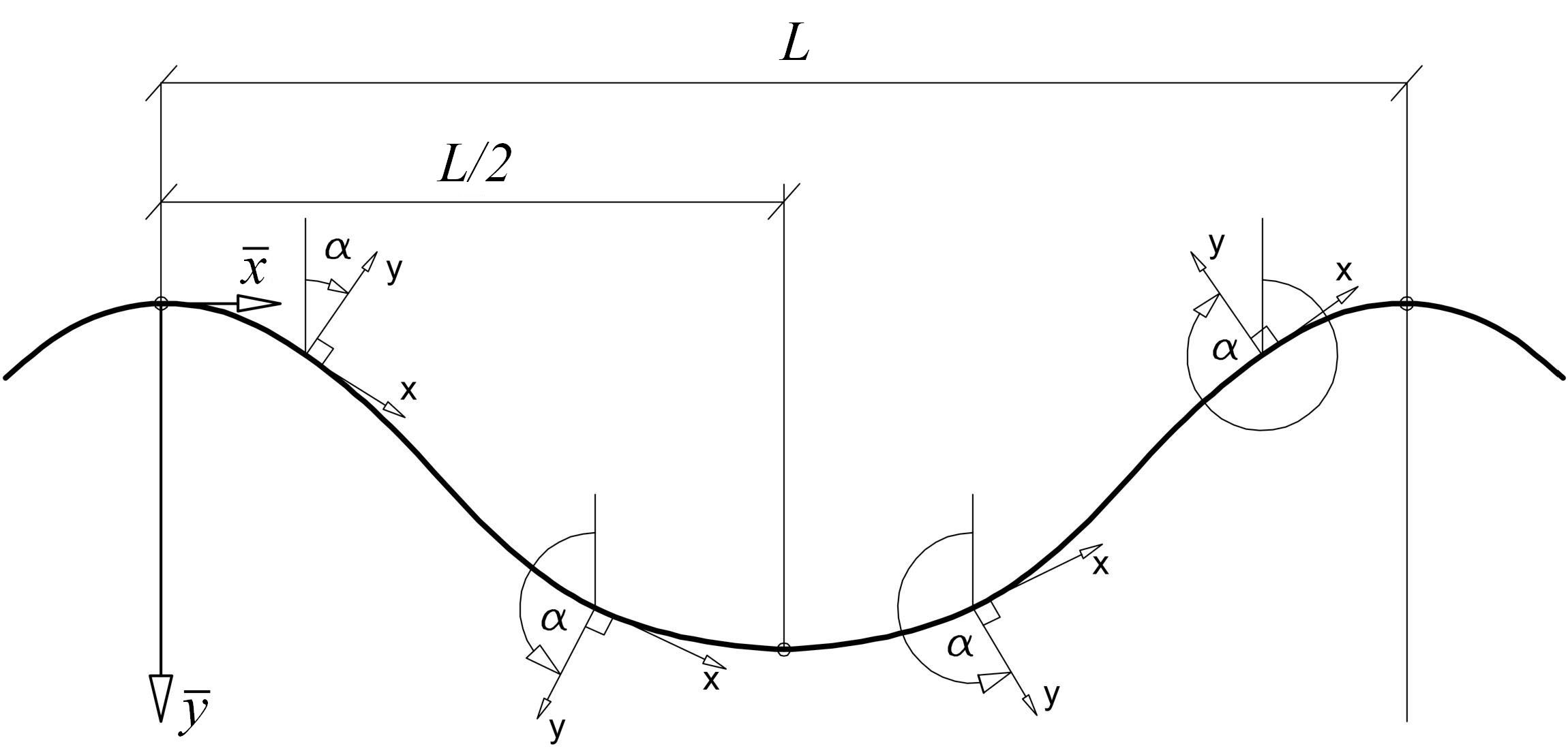
Рисунок 1 - Локальные системы координат

DOI:10.23670/IRJ.2023.138.199.1

Так как в (2) входит производная скорости, то постоянная ее составляющая не влияет на равенство. Для периодической волны такой составляющей является перемещение контура волны в целом, то есть фазовая скорость. Рассмотрим траекторию движения частицы жидкости единичного объема (или, что то же самое, – массы ) без учета фазовой скорости (рис. 1), для краткости ниже будем называть ее «траекторией». Система координат наблюдателя (рис. 1) перемещается с постоянной скоростью, равной фазовой скорости волны. 

Перепишем (2) без учета фазовой составляющей скорости в предположении ламинарности потока для проекций на оси одной из местных систем координат (рис. 1), в которой ось ортогональной системы координат направлена по касательной к траектории (то есть сонаправлена вектору ), ось в точках отрицательной кривизны направлена по нормали к траектории по направлению внешнему к потоку, в точках положительной кривизны – по направлению противоположному внешнему к потоку:

(3)

Где угол – угол с осью от противоположного направления вертикально вниз направленной силы тяжести, измеряемый по часовой стрелке в точках отрицательной кривизны и против часовой в точках положительной кривизны. Угол – угол вектора градиента давления с осью . – знакопеременный радиус кривизны в рассматриваемой точке, того же знака, что знак кривизны

В левой части второго равенства (3) проекцию ускорения на ось , перпендикулярную траектории, мы приравняли центростремительному ускорению, соответствующему радиусу кривизны  

где – единичные векторы вдоль осей локальной системы координат (рис. 1) соответственно.

Таким образом определенные местные системы координат позволяют каждой точке траектории в пределах одного периода, где выполняется (3) и следовательно выполняется (2), сопоставить единственное значение , . Поэтому в (3) его слагаемые и величины являются функциями . Очевидно, что сам угол является функцией времени . Зависимость угла от угла исследуется ниже. В точках, где , центростремительное ускорение и левая часть второго равенства (3) равны нулю, поэтому правая часть второго равенства (3) равна нулю независимо от выбранного направления оси (рис. 1). То есть, мы постулировали вид геометрии поверхности волны (рис. 1) для постановки задачи и пытаемся подобрать физически не противоречивое соотношение входящих в (3) величин. Если это удастся, будет смоделирована поверхностная линия траектории частицы жидкости единичного объема ламинарного потока. Если при этом будет удовлетворено уравнение непрерывности, то набор таких линий по глубине будет моделировать периодический ламинарный поток волны идеальной тяжелой несжимаемой жидкости.

Так как волны периодические, и каждой точке траектории в рамках периода соответствует единственное значение , , то входящие в (3) величины – периодические функции , причем, в диапазон «укладывается» один период, то есть период меньше или равен . Так как вторые слагаемые (3) имеют период , то остальные слагаемые также имеют период . То есть, имеют представление

(4)

где – константы.

Из (3) очевидно, что в представлении (4) вторых слагаемых правых частей (3) параметр , то есть для них оно совпадает с (5).

(5)

где – константы. Из постулированного нами вида геометрии волны (рис. 1) (то есть вида граничной поверхности ламинарного потока) следует, что периодическая с периодом функция имеет в представлении (4) параметр (5). Поэтому центростремительное ускорение , равное левой части второго равенства (3), является периодической с периодом функцией, если скорость равна (6).

(6)

где – константа , а функция имеет представление (5).

Действительно, для того, чтобы центростремительное ускорение было конечно, необходимо, чтобы функция была равна нулю в тех же точках , что функция :

(7)

Выполняя требование (7), почленно сравнивая представление (5) функции с представлением (4) функции при , , , получим (6). В соответствии с изложенным ниже случай рассмотрен как предельный от случая .

Из двух предыдущих абзацев следует, что первое слагаемое правой части второго уравнения (3) также должно иметь представление (5). Это возможно, если

(8)

или

(9)

или

(10)

Рассмотрим правую часть первого равенства (3) варианта (8):

(11)

Из (11), (6) следует, что вариант (8) для выполнения первого равенства (3) невозможен: производная по от вида (5) не может иметь постоянного слагаемого правой части (11).

При вариантах (9), (10) правая часть первого равенства (3) – сумма тригонометрических функций с постоянными множителями. Следовательно, левая часть первого равенства (3) также сумма тригонометрических функций с постоянными множителями. Следовательно, так как вида (5), то – константа, то есть

(12)

где – константа, .

Если справедливо (9), то 

(13)

где – константы, такие, что , , то есть

(14)

или

(15)

В вариантах (13), (14) или (15), давление на оси по глубине не меняется. Получаем противоречие с физическим смыслом. Поэтому для поверхностной траектории физически единственно возможным является вариант (10) когда уравнения (3) преобразуются к виду

(16)

где

(17)

– константы,

(18)

Кроме равенств (17), (18) касательная скорость и радиус связаны величиной угловой скорости, то есть

(19)

где – угловая скорость. С учетом принятых знаков и из (6), (19) получим

(20)

Так как – константа, от не зависит, из (19), (20) следует

(21)

Из первого равенства (16), (17), (21) следует

(22)

Таким образом

(23)

(24)

Из второго равенства (16), (23), (24) следует

(25)

то есть градиент давления направлен по нормали к траектории и является константой (когда траектория совпадает с поверхностью волны, давление на ней равно атмосферному принятому постоянным).

Полученные представления справедливы не только при непрерывном изменении аргумента в диапазоне: , но постулированная нами геометрия (рис. 1) допускает наличие разрывов аргумента в точках нулевого радиуса кривизны . В этом варианте в точке , , функция имеет скачек значений: предельное значение при стремлении слева, , равно , а при стремлении справа равно . На длине половины волны каждая из функций (23), (24), (25) «распадается» на две функции с областями аргумента: , , заданных в местных системах координат (рис. 1), в которых при и значения радиуса кривизны равны нулю (24), что соответствует равным по модулю и противоположным по знаку значениям параметра . То есть, эти две функции «сшиты» в точках равного нулю радиуса , где задаваемые ими участки траектории имеют совпадающую касательную и косую симметрию относительно точки . При этом градиент давления (25) остается постоянным на всей «сшитой» траектории, так как изменение его знака происходит в местной системе координат. С помощью косой симметрии относительно точки определяется половина волны, в свою очередь с помощью симметрии относительно точки определяется целая волна (поэтому случай в (7) соответствует пределу ).

Так как 

(26)

где – период, то, задавая и , мы определяем траекторию. Действительно, зная , определяем из (26) и параметр из (27).

(27)

Эти параметры определяют четверть траектории и, следовательно, всю траекторию через описанную выше симметрию.

Координаты точек поверхности волны (рис. 1), соответствующие четверти волны: , задаются выражениями:

(28)

(29)

Высота траектории равна 

(30)

длина траектории равна 

(31)

Из (30), (31) следует, что при заданном значении наибольшая амплитуда при . В таблице 1 приведены значения максимальных длины и высоты волны в зависимости от периода , что соответствует . Так как амплитуда траекторий одной длины волны с глубиной уменьшается, то соответствующее значение , , уменьшается. Следовательно, заданные значения определяют не только поверхностную, но и все последующие траектории по глубине ламинарного потока.

Действительно, длина волны и значение поверхностной траектории определяются (26), (27), (31), уменьшая значение от максимального на поверхности до нуля, можно определить при постоянной значение каждой последующей траектории из (31). Так как при значение скобок (31) стремится к нулю, то , модули радиусов (24) стремятся к бесконечности.

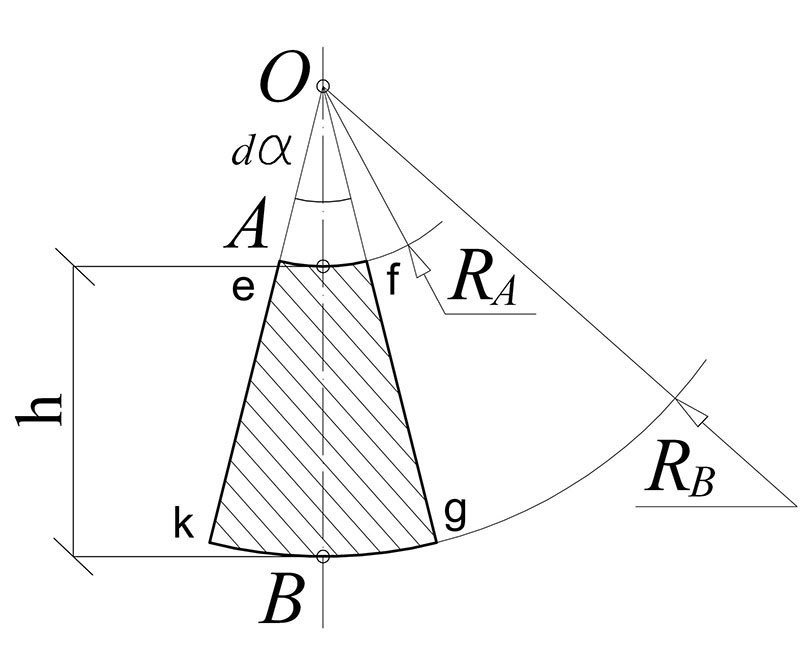
Рисунок 2 - Определение расстояния h между траекториями

DOI:10.23670/IRJ.2023.138.199.2

Определим положение каждой траектории по глубине. Рассмотрим сегмент (рис. 2) с осью симметрии на которой (рис. 1). Ламинарный поток несжимаемой жидкости, скорость которого связана с радиусом пропорцией: , (23), (24), может существовать вблизи только в рамках сегмента (рис. 2).

Действительно, чтобы траектории не пересекались, необходимо и достаточно, чтобы дуги радиусов в каждой точке имели совпадающий центр , тогда пройденный за время вдоль каждой траектории путь от до равный

пропорционален радиусу дуги с центром (рис. 2), и эти пути не пересекаются (21). Из этого условия определяется расстояние .

Таблица 1 - Максимальные длина и высота волны в зависимости от периода T

DOI:10.23670/IRJ.2023.138.199.3

Рисунок 3 - Первые 16 траекторий волны периода 8 сек и длиной L = 49,94 м с параметрами – таблица 2

DOI:10.23670/IRJ.2023.138.199.4

Таблица 2 - Параметры траекторий – рисунок 3

DOI:10.23670/IRJ.2023.138.199.5

В предположении потенциальности потока проекции скорости на оси ортогональной системы координат, связанной с Землей, где ось параллельна оси , а ось параллельна оси (рис. 1), должны быть производными от некоторой гармонической функции (32)

[16]

.

(32)

В точках оси проекция равна нулю: , так как эта ось перпендикулярна траекториям (рис. 1) и фазовой скорости. Следовательно, в этих точках (32):

(33)

где – константа, значения скорости постоянны и равны , то есть , где – фазовая скорость равная константе. Очевидно, что построенное решение условиям (32), (33) не удовлетворяет, поэтому моделируемый поток не является потенциальным.

Для фазовой скорости должно выполняться условие

(34)

где – максимальное по модулю значение орбитальной скорости (23) в точках оси (рис.1), равное значению в самой высокой точке волны.

Покажем. что предложенная модель удовлетворяет уравнению Эйлера

Уравнения (16) – уравнения выполнения законов классической механики в местной (движущейся вместе с единичным объемом) системе координат. То есть, уравнения (16) заменяют собой (обеспечивают выполнение) уравнение Эйлера, так как уравнение Эйлера – следствие законов классической механики в глобальных, связанных с Землей координатах, а (16) – выполнение тех же законов в локальных координатах, перемещающихся вместе с частицей жидкости единичного объема.

При условии (34) кривую, четверть которой задана координатами (28), (29), а половина и целая описанной выше симметрией, можно рассматривать как траекторию перемещения частицы жидкости единичного объема, массы ρ в рамках одного цикла периодической волны. В то же время ее можно рассматривать как геометрическое место точек частиц жидкости единичного объема массы ρ в заданный момент времени . При этом в каждой точке кривой в каждый момент времени приток жидкости равен оттоку.

Так как аналогичную кривую с той же длиной волны можно провести через любую точку моделируемого потока, то бесконечный набор таких кривых, связанных соотношением радиусов (рис. 2), задает геометрическое место точек частиц жидкости в заданный момент времени одного цикла волны в целом. Где в каждой точке в каждый момент времени приток жидкости равен оттоку, следовательно, выполняется уравнение непрерывности

В качестве примера на (рис. 3) приведены первые 16 траекторий волны с периодом 8 сек и длиной L = 49,94 м на половине волны.

Значения таблицы 1 получены из условия . Из того, что наблюдаемых высот волн больше значений третьего столбца таблицы 1 не зафиксировано, следует, что для волн большего периода и длины физически реализуется вариант поверхностной траектории при .

Есть наблюдения одиночных волн большой амплитуды, «встроенных» в периодический волновой процесс «обычной» амплитуды, о так называемых «волнах-убийцах»

До этого момента мы неявно предполагали бесконечную дифференцируемость траектории, откуда следует используемая выше косая симметрия двух четвертей волны, составляющих половину волны. Если мы ослабим это условие до существования второй производной, то есть, до непрерывности радиуса кривизны траектории, уравнения (16) также будут выполняться. При этом станут возможны варианты, при которых смежные гребень и впадина будут соответствовать двум разным волнам, полученным из условия бесконечной дифференцируемости траектории.

Действительно, непрерывность функции соответствует непрерывности радиуса кривизны траектории в точке , . Этого достаточно для «склейки» гребня одной волны с бесконечно дифференцируемой траекторией со впадиной другой волны с бесконечно дифференцируемой траекторией, при этом уравнения (16) выполняются. Сила тяжести – бесконечно дифференцируемая функция времени, поэтому левая часть первого уравнения (16) также должна быть бесконечно дифференцируемой, как и правая. Однако, не учтенные в модели физические факторы, в частности воздействие ветра или разницы температур на разных высотах, могут привести к однократному или постепенному росту модуля разности величины потенциальной энергии в точках и , или модуля разности величины потенциальной энергии в точках и . Так как градиент давления перпендикулярен траектории, работу в рамках модели совершает только сила тяжести, следовательно, этот модуль будет равен произведению ускорения свободного падения на разницу высот в точках и , или в точках и . То есть, приток энергии будет трансформироваться в увеличение высоты гребня или впадины. Этот аномальный гребень или впадина будет продолжать существовать «встроенным» в поток периодических волн «обычной» амплитуды, до тех пор пока бесконечная дифференцируемость по времени слагаемых уравнений (16) не будет восстановлена.

Приведена модель периодических поверхностных волн идеальной тяжелой несжимаемой жидкости, в отличие от большинства известных не предполагающая потенциальность ламинарного потока. Проведенный анализ показал, что в рамках модели поток не является потенциальным. Модель допускает существование аномально высоких волн, «встроенных» в поток периодических, так называемых «волн-убийц».