INTEGER PARAMETERIZATION OF GEOMETRIC SHAPES ON THE COORDINATE PLANE
INTEGER PARAMETERIZATION OF GEOMETRIC SHAPES ON THE COORDINATE PLANE
Abstract
When describing visualization objects by a set of characteristic (reference) points, the geometrical shape of objects is restored by means of interpolation. As a rule, parametric interpolation with application of mixing functions is used. The efficiency of interpolation to a great extent depends on the choice of parameter values in the reference points. Using spline interpolation as an example, researchers have shown that chordal and centripetal parameterization produce favourable visual shapes. However, they have disadvantages. These are, firstly, the organization of the interpolation process separately by segments, and the range of parameter values for each segment is different and is represented by a set of real numbers. This complicates the algorithm and reduces the interpolation performance. The paper proposes interpolation with integer counts of the parameter. These samples are defined on the argument plane of the interpolant. An algorithm for finding the counts is described. The paper presents the results of an experimental comparison of the possibilities of integer and centripetal parameterization on the example of a plane curve. The experiment has shown that the integer parameterization is not inferior to centripetal parameterization in accuracy at rational choice of distances between reference points. At the same time, the integer parameter values are arguments of mixing functions, the values of which can be quickly found by the tabular method.
1. Введение
В задачах геометрического моделирования объектов визуализации исходными данными, зачастую, являются неупорядоченные множества характерных (опорных) точек. Тогда поверхность объекта восстанавливается интерполяционными методами. В качестве примеров можно назвать визуализацию результатов 3D-сканирования объектов, построение поверхностей по точкам, заданным разработчиком, создание рельефа земной поверхности по замерам топографов, отображение тенденции поведения физической величины по набору дискретных отсчетов (например, по сигналам датчиков), наглядное представление экспериментальных данных. В этих случаях традиционно применяются методы интерполяции на основе смешивающих функций: метод обратных взвешенных расстояний, метод Шепарда, различные виды сплайн-интерполяции, триангулированная нерегулярная сеть, радиальные базисные функции и другие. Им посвящен целый ряд публикаций разных лет, в частности , , , . Опорные точки становятся узлами интерполяции. В процессе интерполяции координаты текущей точки определяются как взвешенные значения смешивающих функций, которые привязаны к опорным точкам. Можно представить, что каждая опорная точка вносит в координаты текущей точки некоторый вклад, зависящий от взаимного расположения этих точек.
Поверхности объектов могут иметь сложную геометрию, в связи с чем функция-интерполянт записывается в параметрической форме:
где x, y, z – декартовы координаты текущей точки;
N – количество опорных точек;
bf (u,v) – смешивающая функция;
u, v – параметры (аргументы функции-интерполянта);
– весовые коэффициенты – коэффициенты влияния i-го узла интерполяции на декартовы координаты текущей точки.
Систему параметрических координат u, v можно представить в виде криволинейной сетки, «наброшенной» на поверхность. Узлы параметрической сетки привязываются к опорным точкам и являются узлами интерполяции. Для получения интерполяции с малой погрешностью важно рационально назначать опорным точкам значения параметрических координат.
2. Методы и принципы параметризации геометрических форм
Расстановка опорных точек в области определения поверхности может характеризоваться значительной неравномерностью. Если количество узлов параметрической сетки совпадает с количеством опорных точек, то расстояние между соседними опорными точками равно одной параметрической единице. Из-за этого появляются нежелательные аномалии. Дело в том, что для компьютерной визуализации объекты представляются в полигональной форме. Если привязывать полигоны к ячейкам координатной сетки, то на участках сгущения опорных точек возникнет много мелких полигонов, хотя прикладная задача может и не требовать такой детальности. Кроме того, на таких участках могут возникать выбросы координат и петли, что неприемлемо для визуальных образов потенциально гладких поверхностей. С другой стороны, на участках с редкой расстановкой опорных точек возникнут обширные плоские участки, что придает поверхности стилизованный («граненый») вид.
Выходом является сопоставление параметрических координат опорных точек с их пространственным размещением. Такой способ для случая параметризации кривых предложен еще в 1989 году. В работе исследуются отличия двух разновидностей параметризации – хордовой (chordal) и центростремительной (centripetal) от традиционной – равномерной (uniform). Исследование проводится на примере интерполяции кубической кривой. В диссертационной работе А.Ю. Якимович показано, что и хордовая, и центростремительная параметризации имеют достоинства и недостатки, а лучшей параметризацией кривой является естественная, или натуральная параметризация – параметризация длиной дуги. Приближением к естественной параметризации является хордовая параметризация. К такому же выводу пришли авторы статьи , исследовавшие возможные виды параметризации для применения кардинального сплайна в задачах анимации. В работе рассматриваются геометрические свойства квадратичных интерполяционных кривых Безье с равномерной и центростремительной параметризацией, показаны достоинства центростремительной параметризации. Рекомендации по применению названых видов параметризации кривой Безье в задаче отображения дорог на карте изложены в статье . В работе на примере сплайна Кэтмулла-Рома математически доказывается, что центростремительная параметризация имеет преимущество в части качества интерполяции. Авторы статьи также считают, что одной из наиболее эффективных и, вероятно, наиболее часто используемой является центростремительная параметризация. Эксперимент, как правило, подтверждает этот вывод, например, в .
Параметрические расстояния между соседними опорными точками кривой в описываются выражением
где в двойных прямых скобках – декартово расстояние между двумя последовательными точками
– их параметрические координаты, причем
α – показатель степени, зависящий от вида параметризации.
Для равномерной параметризации α=0, для хордовой – α=1, для центростремительной – α=1/2. Смысл центростремительной параметризации прост: для близко расположенных точек приращение параметрических координат увеличивается по сравнению с декартовым расстоянием, а для далеко разнесенных точек это приращение уменьшается. Действительно, для имеет место соотношение
а для имеет место
Если на единице параметрической системы координат организовать фиксированное число геометрических примитивов (для кривых это линейные отрезки), то их количество на участках сгущения опорных точек увеличивается, а на участках разрежения – падает. Это соответствует логике расстановки опорных точек: на участках рельефа с мелкими деталями опорных точек должно быть больше, на ровных участках – меньше. В утверждается, что центростремительная параметризация не допускает образования петель и приближает кривую к ломаной, соединяющей опорные точки. Однако для интерполяции поверхности такой вид параметризации применить весьма затруднительно.
Параметризация поверхностей – одна из сложных задач геометрического моделирования. В принципе, есть две задачи: параметризация реального объекта (или его модели) и параметризация по множеству точек, принадлежащих поверхности объекта. В первом случае разработчик сам определяет размещение параметрической сетки на поверхности объекта. Поверхность, зачастую, уже задана чертежами или каркасной моделью. Например, в статье описана хордовая параметризация в узловых точках каркаса. Сравнительный анализ применения равномерной, хордовой и центростремительной интерполяции на опорных точках B-сплайновой поверхности, заданной сеткой опорных точек, приведен в . В работе говорится о параметризации строительных форм, которые существуют в виде реального проекта. Процесс такой параметризации во многом формализован и реализован в виде программного обеспечения САПР, например, в популярном моделере Altair HyperMesh . Существует целый спектр методов параметризации реальных объектов, и этим методам посвящена обширная библиография. Например, в статье 2005 года авторы проанализировали 78 статей на эту тему и констатировали интенсивный рост числа публикаций в дальнейшем. Причина такого роста в том, что в зависимости от конкретных требований, предъявляемых практическими приложениями, для задания параметризации используются различные ограничения. Типичными примерами ограничений являются точечные ограничения, ограничения кривизны и топологические ограничения. Ряд алгоритмов параметризации поверхностей с учетом ограничений рассмотрен в диссертационной работе Hanxiao Shen .
Вторая задача – параметризация поверхности по множеству опорных точек – имеет множество решений, что равнозначно отсутствию универсального решения. Поэтому здесь тоже приходится учитывать ограничения и указания разработчика. В частности, в работе специалистами предлагается параметризация вдоль линий сечения поверхности, что сводит задачу к параметризации кривых. В этом случае, как уже отмечалось, в качестве параметра следует использовать длину дуги между опорными точками. Однако, как справедливо утверждается в работе , интерполируемая кривая заранее не известна, поэтому следует выбирать хордовую параметризацию.
Как видно из приведенного обзора публикаций, авторы в зависимости от прикладной задачи рекомендуют и хордовую, и центростремительную параметризацию. У них есть общее свойство: последовательное вычисление параметрических координат по выражению (2) возможно только тогда, когда известен порядок размещения опорных точек на геометрической форме. В случае кривой он определяется достаточно просто: либо с помощью сортировки точек по их декартовым координатам, либо с помощью указаний разработчика. В случае поверхности неравномерность расстановки опорных точек приводит к тому, что результат сортировки дает упорядочение точек, непригодное для применения традиционной, например, сплайновой, интерполяции. В случае применения центростремительной и хордовой параметризации интервал между каждой парой опорных точек нужно вычислять отдельно и организовывать его разбиение на различное число участков для визуализации. Кроме того, выражение (2) дает параметрические координаты опорных точек в виде вещественных чисел. Вычисление значений интерполянта в этом случае замедляется, особенно если учесть, что в прикладных задачах визуализации опорные точки исчисляются сотнями и тысячами.
3. Целочисленная параметризация на плоскости
Предлагается целочисленная параметризация поверхности на плоскости аргументов. Основой параметризации является сетка целочисленных координат u, v. Она не совпадает с исходной сеткой координат декартова пространства, а ее детальность выбирается, исходя из плотности расположения опорных точек. Организуется перебор опорных точек причем последовательность перебора не важна. Каждая точка «привязывается» к ближайшему узлу параметрической сетки и тем самым получает пару координат u, v, которые находятся по выражениям
где квадратные скобки означают округление до ближайшего целого;
U, V – максимальные количества отсчетов по координатам u и v;
– границы области определения реконструируемой поверхности.
Процесс нахождения параметрических координат можно образно представить как изгибание исходных координатных линий u, v таким образом, чтобы опорные точки попадали в узлы параметрической сетки. Возникает криволинейная сетка на плоскости xy, эту сетку можно считать проекцией на плоскость криволинейной ортогональной пространственной системы параметрических координат.
В процессе нахождения параметрических координат по выражениям (3) возможна аномалия: две и более точек могут получить одинаковые целочисленные координаты. Аномалия устраняется одним из двух приемов. Во-первых, можно ввести более частую сетку параметрических координат, то есть увеличить U, V. Во-вторых, совпадающие точки можно заменить одной – с усредненной координатой высоты. Тем самым проводится редукция числа опорных точек и решается проблема излишне высокой детальности модели поверхности.
Теперь каждая i-я опорная точка получает пять координат: три декартовы и две параметрические
, причем параметрические координаты являются целыми числами. Такая параметризация выполняется заранее, не в режиме реального времени. Полученные координаты являются исходными данными для реконструкции поверхности с помощью интерполяции. Опорные точки на параметрической сетке расставлены в соответствии с их декартовыми координатами. Расстояния между соседними опорными точками находятся в плоскости аргументов x, y, то есть являются проекциями хорд, соединяющих соседние опорные точки в пространстве. Поэтому предложенную параметризацию можно назвать целочисленной хордовой параметризацией на плоскости. Описанный способ параметризации применим к однозначным поверхностям, у которых каждой паре значений аргументов может соответствовать не более одной пространственной точки. Это ограничение предлагаемой параметризации. Реальные поверхности могут быть многозначными. Их приходится разбивать на однозначные фрагменты и проводить их параметризацию раздельно. Вариант методики выделения фрагментов описан в работе .
Из-за различных расстояний между опорными точками не все узлы параметрической сетки оказываются занятыми. Чтобы можно было применить для реконструкции поверхности любой метод интерполяции, следует расставить дополнительные опорные точки в свободных узлах сетки. Для этого предлагается применить параметрическую интерполяцию на основе смешивающих функций ортогонального базиса (СФОБ) и табличных вычислений. СФОБ представляют собой комбинацию из двух смешивающих функций и отличаются тем, что действуют раздельно вдоль параметрических координат, благодаря чему каждый компонент СФОБ зависит только от одной параметрической координаты . Табличные вычисления СФОБ могут быть применены, благодаря целочисленным отсчетам параметрических координат.
Интерполянт записывается в виде трех параметрических уравнений вида (1):
где – СФОБ i-й опорной точки, действующие вдоль координат u и v, соответственно;
– аргументы СФОБ – расстояния между текущей точкой и i-й опорной точки вдоль координатных линий u, v:
u, v – параметрические координаты текущей точки поверхности;
– коэффициенты влияния i-й опорной точки на декартовы координаты текущей точки.
Значения коэффициентов находятся из условия точного прохождения реконструируемой поверхности через опорные точки. Смысл условия таков: если в качестве текущей точки в систему (4) подставить параметрические координаты опорной точки, то вычисленные по (4) значения должны совпасть с декартовыми координатами этой опорной точки. Условие должно быть справедливым для всех опорных точек. Условие записывается в виде системы уравнений:
где – параметрические расстояния между i-й и j-й опорными точками.
Каждое уравнение системы (5) разворачивается в систему из N линейных алгебраических уравнений (СЛАУ), неизвестными в которых являются коэффициенты (i=1..N). Решение СЛАУ одним из известных методов (Гаусса, Крамера, LU-разложения или другим) дает значения коэффициентов влияния исходных опорных точек. Для уменьшения числа слагаемых в уравнениях СЛАУ следует применять СФОБ, локализованные в пространстве, то есть такие, значения которых убывают с удалением от опорной точки и при каком-то удалении могут не учитываться (обнуляются). Примером такой СФОБ является биквадратная (расстояния
приведены к размеру зоны влияния опорной точки):
Подстановка найденных коэффициентов влияния опорных точек в систему (4) дает интерполянт. Для заполнения узлов параметрической координатной сетки нужно организовать последовательный перебор этих узлов в диапазонах координат u = 0 .. U, v = 0 .. Vи для каждого узла найти декартовы координаты из системы (4). Они принимаются за координаты новых опорных точек. Следует отметить, что все расстояния в процессе интерполяции получаются целочисленными. Это дает возможность применить быстрые табличные вычисления смешивающих функций. Их значения вычисляются заранее с некоторым шагом и заносятся в память компьютера. Целочисленные расстояния
после приведения к диапазону адресов памяти используются для считывания из нее значений смешивающих функций.
Получено множество новых, регулярно расставленных опорных точек. Они могут использоваться в качестве вершин полигональной сетки или служить опорными точками следующего этапа интерполяции. Следующий этап может быть направлен на интерполяцию в режиме реального времени. Например, сплайн-интерполяция на каждом шаге использует гораздо меньше вычислений, чем интерполяция с применением радиальных или ортогональных базисных функций. Выделение наборов опорных точек, необходимых для формирования сплайновых сегментов, на регулярной ортогональной сетке не представляет труда. Остается показать, что интерполяция с применением целочисленной параметризации на плоскости не уступает по точности другим видам интерполяции.
4. Экспериментальное исследование возможностей целочисленной параметризации
Целочисленную параметризацию нужно сравнивать с лучшими известными методами. Например, высокое качество центростремительной параметризации, обоснованное в работе , делает целесообразным сравнение именно с ней. Поскольку описание центростремительной параметризации относится к плоской кривой, экспериментальное исследование целочисленной параметризации также проведено для плоской кривой. Это не влияет на применимость параметризации к поверхности, поскольку, как отмечалось выше, поверхность может строиться на основе криволинейных сечений. В этом случае в качестве аргумента интерполянта используется одна параметрическая координата. Для целочисленной параметризации ее ось совпадает с осью x.
Исследование параметризации проведено на примере тестовой кривой, имеющей следующее описание
где t – параметр построения кривой (параметр интерполяции будет обозначен буквой s).
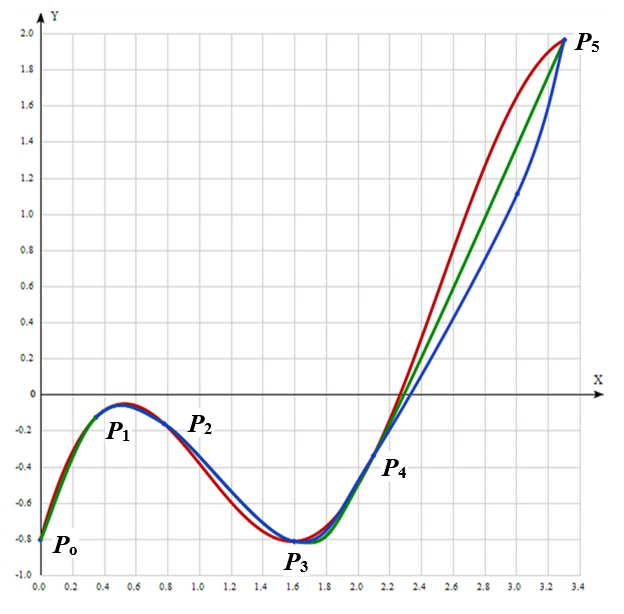
Рисунок 1 - Два вида интерполяции тестовой кривой по шести опорным точкам
Таблица 1 - Декартовы и параметрические координаты опорных точек
| P0 | P1 | P2 | P3 | P4 | P5 |
t | 0 | 1.17 | 2.60 | 5.33 | 7.00 | 11.01 |
x | 0 | 0.35 | 0.78 | 1.60 | 2.10 | 3.30 |
y | -0.805 | -0.127 | -0.163 | -0.814 | -0.340 | 1.963 |
si-cent | 0 | 0.873 | 1.530 | 2.553 | 3.383 | 4.995 |
si-int | 0 | 1 | 2 | 5 | 6 | 10 |
λxi | 90.07 | 422.51 | -1085.85 | 1961.12 | -1468.85 | 70.41 |
λyi | 1447.91 | -2188.62 | -453.63 | 4862.33 | -3911.64 | 195.72 |
Для интерполяции кривой с применением центростремительной параметризации, как и в работе , использован сплайн Кэтмулла-Рома. Сплайновая кривая строится по отсекам. В рассматриваемом случае их должно быть пять. Каждый отсек описывается четырьмя опорными точками. В матричной форме описание отсека имеет вид:
где S – матрица-строка степеней параметра, в которой smin и smax – начальное и конечное значения параметра в пределах одного отсека:
MCR – базисная матрица Кэтмулла-Рома:
X, Y – матрицы-строки декартовых координат опорных точек отсека:
Свойство сплайна Кэтмулла-Рома таково, что при «пробегании» аргументом диапазона от минимального до максимального значения рассчитывается участок кривой между двумя средними точками. Чтобы восстановить крайние отсеки тестовой кривой, нужно применить для сплайновой кривой кратные крайние опорные точки, то есть строить первый отсек на опорных точках P0, P0, P1, P2, второй отсек – на точках P0, P1, P2, P3, третий – на точках P1, P2, P3, P4, четвертый – на точках P2, P3, P4, P5 и пятый – на точках P3, P4, P5, P5. В пределах каждого отсека параметр s изменяется в своем диапазоне: для первого отсека – в диапазоне [0, 0.873], для второго – в диапазоне [0.873, 1.530], далее – в диапазонах [1.530, 2.553], [2.553, 3.383], [3.383, 4.995], как это видно из таблицы 1. Кривая, полученная в результате интерполяции сплайном Кэтмулла-Рома, показана на рисунке 1 зеленой линей.
Для интерполяции с целочисленной параметризацией использована биквадратная СФОБ (6). В случае интерполяции плоской кривой используется один параметр s, и параметрическая запись интерполянта получается в результате упрощения системы уравнений (4):
где si-int – целочисленная параметрическая координата i-й опорной точки;
si-inf – половина симметричной области влияния опорной точки вдоль оси параметра.
Целочисленные параметрические координаты si-int опорных точек найдены по первому выражению (3) с учетом замены u на s и занесены в таблицу 1. Значения коэффициентов влияния λxi, λyi определены из условий точного прохождения реконструируемой кривой через опорные точки. Условия получены упрощением (5). Например, для координаты x эти условия выглядят так:
– прохождение кривой через P0,
– прохождение кривой через P1, ...
– прохождение кривой через P5,
при этом параметр принимает значения координат опорных точек: s=0, 1, 2, 5, 6, 10.
Значение sinf принято равным 12 для того, чтобы на каждую текущую точку кривой влияли все опорные точки, поскольку их количество мало. Аналогично составлена СЛАУ для отыскания значений λyi. Системы уравнений решены методом Крамера, в результате получены значения коэффициентов влияния опорных точек, показанные в таблице 1. Они подставлены в математическое описание интерполянта (7), по которому найдены промежуточные точки кривой. Кривая, реконструированная с применением СФОБ и целочисленной параметризации, показана на рисунке 1 синим цветом.
5. Обсуждение
Анализ полученных результатов показывает:
- форма кривой, полученной с применением целочисленной параметризации (ЦП-кривой), соответствует тестовой кривой и кривой, составленной из отсеков сплайна Кэтмулла-Рома (КР-кривой);
- на участках с небольшими расстояниями между опорными точками (P0 – P1,P1 – P2) ЦП-кривая и составная КР-кривая практически совпадают. Для иллюстрации на рисунке 1 первый отсек КР-линии (зеленого цвета) наложен поверх ЦП-кривой, а второй отсек расположен под синей ЦП-линией;
- на участках с большими расстояниями между опорными точками (P4 – P5) оба интерполянта дают значительную погрешность, причем погрешность интерполяции с целочисленной параметризацией превосходит погрешность сплайна Кэтмулла-Рома. Следует отметить, что и погрешность сплайна на указанном участке кривой слишком велика для практического применения в задачах проектирования и моделирования (приведенная погрешность около 7%). Это говорит о том, что расстояние между опорными точками P4 и P5 задано слишком большим для точной интерполяции.
6. Заключение
Центростремительная параметризация обладает рядом особенностей, из-за которых при выборе имеет смысл отдать предпочтение целочисленной параметризации. К этим особенностям относятся вещественные значения параметрических координат опорных точек. Вещественные значения замедляют интерполяцию в случае большого количества опорных точек. Еще одна особенность – посегментная интерполяция в случае применения составных кривых, например, описываемых сплайнами. Напротив, применение СФОБ не требует раздельной интерполяции кривой по сегментам, а целочисленные приращения параметра при движении по координатной оси позволяют рассчитать значения СФОБ быстрым табличным методом. В то же время целочисленная параметризация не уступает центростремительной параметризации по точности интерполяции, но требует более частой расстановки опорных точек. При выполнении этого условия сочетание целочисленной параметризации и локализованных в пространстве СФОБ позволяет повысить производительность интерполяции без потери качества.
В статье проведено сравнение возможностей двух различных интерполянтов – составного сплайна Кэтмулла-Рома и полиномов на основе СФОБ. Очевидно, далее следует провести исследование интерполяционных возможностей СФОБ с различными видами параметризации как для кривых, так и для поверхностей.
