SYSTEM OF AUTOMATIC SPEED CONTROL OF BELT CONVEYOR ORE CONVEYOR FOR METALLURGICAL PRODUCTION

Ленточные конвейеры – распространенные транспортные средства, применяемые в шахтах и карьерах для транспортирования руды и породы из проходческих, вскрышных, добычных забоев по горизонтальным и наклонным выработкам горных предприятий, для подъёма руды на поверхность с последующим её перемещением к обогатительной фабрике или погрузочному пункту внешнего транспорта, а породы — в отвал

Цель работы – поддержание заданной технологическим процессом скорости движения ленты конвейера при действии возмущающих воздействий для обеспечения производительности.

Математические модели промышленных систем представлены в настоящее время в виде функциональных, структурных схем и направлены на освоение основ теории и практического использования современных методов анализа и синтеза систем на этапах проектирования

[4]

,

[5]

. Функциональная схема системы автоматического управления ленточным конвейером представлена на рисунке рис. 1.

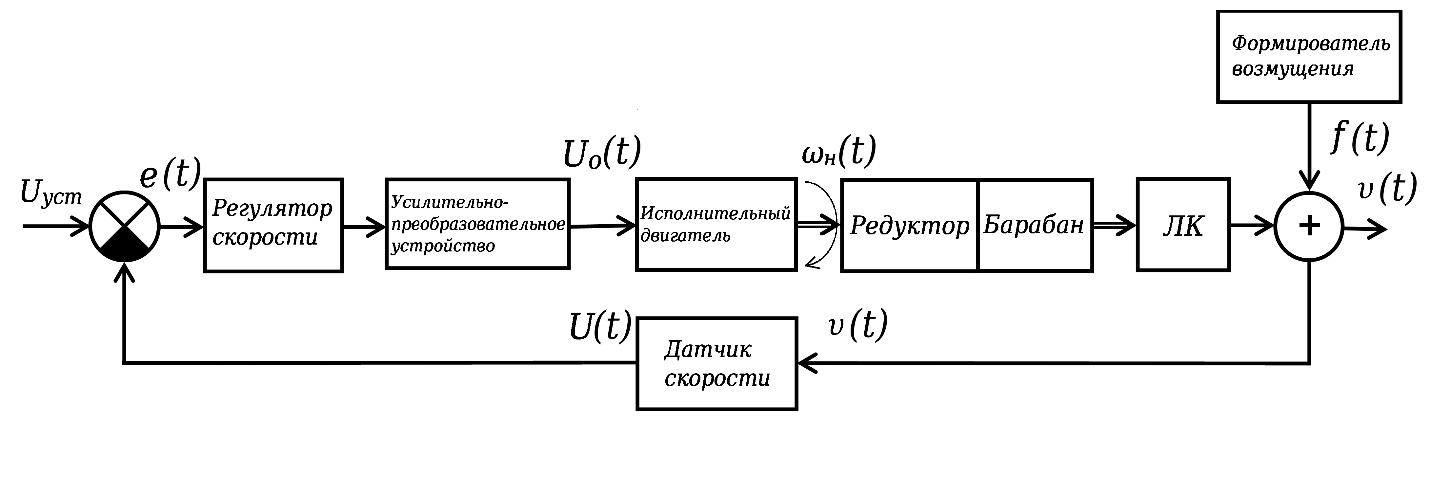
Рисунок 1 - Функциональная схема системы автоматического регулирования скорости ленточного конвейера

DOI:10.23670/IRJ.2023.138.143.1

Функциональная схема содержит следующие элементы и обозначения:

- объект управления - ленточный конвейер ЛК, v(t)- линейная скорость перемещения ленты конвейера;

- исполнительный механизм, включающий двигатель с редуктором, барабаном и усилительно-преобразовательным устройством, ωн (t) – номинальное значение скорости вращения двигателя, U(t) – напряжение обратной связи;

- первичные измерительные преобразователи - датчик скорости

перемещения ленты конвейера и натяжения ленты, U(t) – напряжение пропорциональное скорости движения ленты;

- обобщенный регулятор, вырабатывающий управляющие воздействия по текущей информации о скорости перемещения ленты конвейера и значении заданной скорости;

- задающее устройство, вырабатывающее задающий сигнал Uуст, соответствующий требуемой скорости перемещения ленты конвейера по регламенту технологического процесса;

- f(t) – возмущающие воздействия.

При анализе системы и синтезе регулятора будем использовать линейные модели элементов функциональной схемы в виде их передаточных функций. Обозначим через W0(p) передаточную функцию, включающую описание объекта управления, исполнительного механизма, датчика скорости и натяжения, Wрег(p) передаточную функцию регулятора, и будем считать, что система структурно приведена к единичной обратной связи. Тогда структурная схема системы примет вид, представленный на рис. 2.

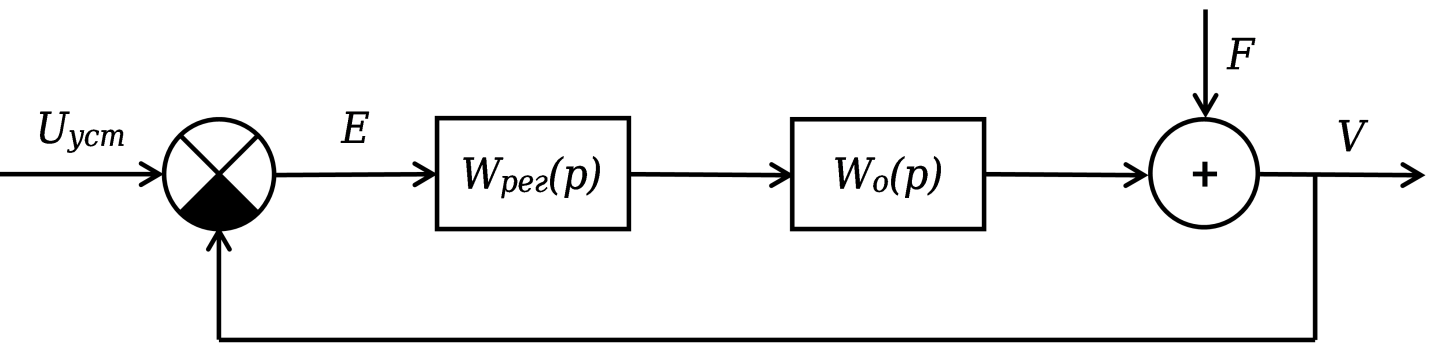
Рисунок 2 - Структурная схема системы

DOI:10.23670/IRJ.2023.138.143.2

Задача синтеза регулятора для системы автоматического регулирования скорости ленточного конвейера заключается в выборе типа регулятора, его структуры и определении значений его параметров, обеспечивающих в замкнутой системе желаемые динамические свойства

[6]

,

[7]

:

- показатели качества переходных процессов в виде времени переходного процесса tп ≤tп*, где tп – время переходного процесса системы, tп* – желаемое время переходного процесса и величины перерегулирования σ ≤ σ*, где σ – перерегулирование системы, σ* - допустимое значение перерегулирования;

- точностные показатели в виде в виде максимально допустимой ошибки eмах отработки заданной скорости конвейера и возмущающих воздействий (перегрузка, недогрузка, растяжение ленты), описываемых в первом приближении гармоническим воздействием вида f(t) = f0sin(ωt), где f0 – амплитуда гармонического воздействия, ω – круговая частота. Параметры возмущающего воздействия ограничены максимально допустимым значением амплитуды f0* (f0 ≤ f0*) и диапазоном изменения круговой частоты ωmin≤ω≤ωmax.

Предлагается для решения поставленной задачи использовать обобщенный регулятор, содержащий две составляющие

 Передаточная функция ПИ составляющей регулятора

(1)

где kи коэффициент передачи интегральной составляющей, kп коэффициент передачи пропорциональной составляющей.

Для данной системы типовым возмущающим воздействием является гармоническое воздействие с максимальным значением амплитуды f0* = 0,2v* и круговой частотой ω0 (f(t) = f0*∙sin⁡ω0t). Моделью, которая генерирует подобное воздействие, является консервативное звено, описание которого задается передаточной функцией внешнего воздействия

(2)

а амплитуда сгенерированного сигнала определяется заданием начальных условий.

Передаточная функция составляющей регулятора с встроенной моделью

(3)

где kв и kм – настроечные параметры регулятора со встроенной моделью, kв –коэффициент передачи по выходной переменной встроенной модели, kм – коэффициент передачи по скорости изменения выходной переменной. Передаточная функция Wвм(p) содержит описание консервативного звена и описание дифференцирующего звена с постоянной времени . Модель, генерирующая гармоническое воздействие частоты ω0 описывается также консервативным звеном, поэтому составляющая с передаточной функцией Wвм(p) консервативного звена, и называют составляющей регулятора со встроенной моделью.

Обобщенный регулятор (рис. 3) формируется как параллельное соединение двух составляющих регулятора и его передаточная функция равна

(4)

где U(p) изображение Лапласа управляющего воздействия, а E(p) изображение Лапласа ошибки – входного воздействия регулятора. Структурная схема обобщенного регулятора представлена на рис. 3.

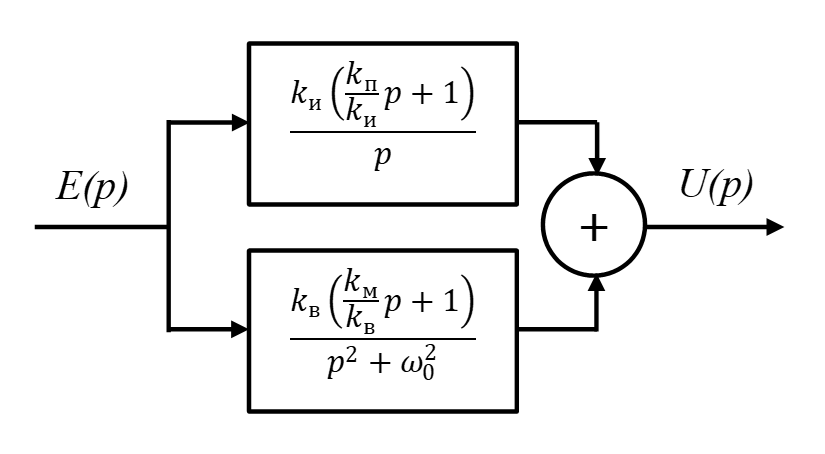
Рисунок 3 - Структура обобщенного регулятора

DOI:10.23670/IRJ.2023.138.143.3

Настроечными параметрами регулятора являются коэффициенты kи, kп, kв и kм. Введение в регулятор составляющей со встроенный моделью возмущающего воздействия позволяет получить в установившемся режиме нулевое значение ошибки отработки возмущающего воздействия, модель которого включена в регулятор. В данном случае, с нулевой ошибкой отрабатывается гармоническое воздействие f(t) = f0* sin ω0t.

Проиллюстрируем приведенные результаты на примере настройки параметров регулятора ленточного конвейера КЛС-800. Передаточная функция W0(p) имеет вид:

(5)

Требуемые показатели качества для системы стабилизации скорости ленты конвейера:

- максимальное значение скорости движения ленты v* = 3м/c

- значение добротности по скорости К*≥10 с-1

- максимально допустимая ошибка отработки заданной скорости конвейера и возмущающих воздействий eмах= 0,05 м/c.

- желаемое время переходного процесса tп* = 0,6 с,

- допустимое значение перерегулирования σ*=30%,

- возмущающее воздействие гармоническое с максимальными значениями амплитуды

f0* = 0,2v* и осредненным значением круговой частоты ω0= 0,314 с-1,

Перепишем передаточную функцию регулятора (4) в виде

и выберем согласно методу настройки на модульный оптимум значения , где Т0max - максимальное значение постоянной времени исходного объекта. Тогда передаточная функция регулятора примет вид

(6)

При этом, постоянная времени дифференцирующего звена регулятора равнаz компенсирует наибольшую постоянную времени постоянной апериодических звеньев объекта.

Отметим, что добротность по скорости рассматриваемой системы, как это следует из вида передаточных функций (5) и(6), равна , поэтому коэффициент kи выбирается из требуемого значения добротности по скорости , a коэффициент .

Соотношение коэффициентов kм и kв равно, откуда следует .Значение коэффициента kв влияет на второй сомножитель числителя передаточной функции регулятора (6), а именно, будет ли этот сомножитель определять передаточную функцию дифференцирующего звена второго порядка, или передаточную функцию двух дифференцирующих звеньев первого порядка. Для того, чтобы данный сомножитель задавал описание двух дифференцирующих звеньев первого порядка значение или . При выборе значения kв = 80 значение kм= 72. Таким образом, настроечные параметры регулятора коэффициенты равны kи = 11 , kп = 10,kв = 80 , и kм = 72.

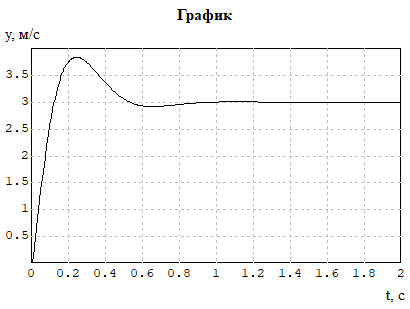
Рисунок 4 - Реакция системы на отработку заданной скорости транспортировки

DOI:10.23670/IRJ.2023.138.143.4

Из графика переходной функции (рис. 4) следует, что заданная скорость движения ленты конвейера 3 м/с при использовании обобщенного регулятора с выбранными параметрами отрабатывает задающее воздействие с временем переходного процесса tп = 0,5 с и перерегулированием σ = 27%, без статической ошибки. Увеличение выбранного значения параметра kв при сохранении соотношения с параметром kм приводит к увеличению значения перерегулирования и времени переходного процесса, а следовательно к не выполнению требуемых показателей качество. Уменьшение значения параметра kв хотя и уменьшает значение перерегулирования, но ухудшает время переходного процесса.

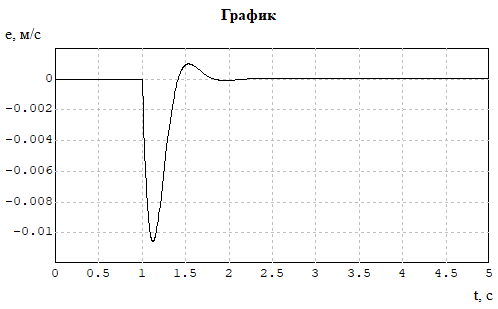
Рисунок 5 - График изменения ошибки e(t) системы с обобщенным регулятором при гармоническом возмущающем воздействии f(t) = 0,6 sin 0,314t

DOI:10.23670/IRJ.2023.138.143.5

Использование встроенной модели гармонического воздействия с частотой ω0 = 0,314 с-1 в обобщенном регуляторе позволяет получить в установившемся режиме в замкнутой системе нулевую ошибку при отработке гармонического воздействия той же самой частоты. (рис. 5)

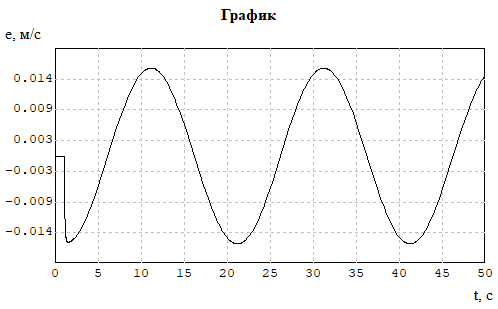
Рисунок 6 - График изменения ошибки e(t) системы ПИ регулятором при гармоническом входном воздействии f(t) = 0,6 sin 0,314t

DOI:10.23670/IRJ.2023.138.143.6

При использовании только ПИ регулятора, как следует из рис. 6, амплитуда максимальной ошибки в установившемся режиме при отработке гармонического воздействия с амплитудой равной 0,6 имеет значение 0,016, то есть подавление возмущающего воздействия происходит в 37 раз.

Рассмотрим, как изменяется ошибка в установившемся режиме при отработке гармонических возмущающих воздействий с частотами, отличающимися от номинальной частоты настройки встроенной модели ω0 = 0,314 с-1. Увеличение значения частоты гармонического возмущения в три раза f(t) = 0,6 sin 0,942t приводит к значению амплитуды установившейся ошибки eу = 0,0019 (рис. 7), то есть подавление возмущающего воздействия происходит в 0,6/0,0019 =315 раз.

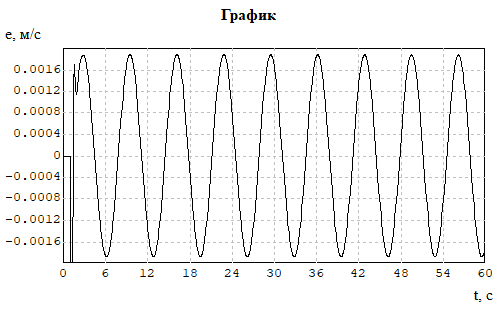
Рисунок 7 - График изменения ошибки e(t) системы с обобщенным регулятором при гармоническом возмущающем воздействии f(t) = 0,6 sin 0,942t

DOI:10.23670/IRJ.2023.138.143.7

При использовании только ПИ регулятора значению амплитуды установившейся ошибки eу = 0,035 м/с, то есть подавление возмущающего воздействия происходит в 17 раз.

Уменьшение значения частоты гармонического возмущения в три раза f(t) = 0,6sin0,105t приводит к значению амплитуды установившейся ошибки eу = 0,0008с-1 и подавление в 750 раз. С ПИ регулятором значение амплитуды установившейся ошибки eу = 0,0055 м/с, подавление возмущающего воздействия происходит в 109 раз. Таким образом можно сделать вывод, что в диапазоне частот ω [0,105, 0,942] амплитуда установившего значения ошибки при отработке возмущающих воздействий f(t) = f0*sinωt не превосходит значения eу* = 0,002 м/с, а подавление возмущения происходит не хуже, чем в 500 раз.

Введение в систему управления конвейером алгоритма достижения требуемых показателей по качеству и точности процесса стабилизации скорости конвейера обеспечивает поддержание скорости на необходимом уровне при наличии возмущающих воздействий, таких как перегрузка, недогрузка, растяжение ленты, неоднородность размеров и массы. Полученный алгоритм управления решает задачу стабилизации скорости ленточного конвейера, компенсации возмущающих воздействий и обеспечивает постоянную производительность.

Поддержание постоянства скорости ленты положительно сказывается на работе конвейера и позволяет обеспечивать необходимую производительность при наличии возмущающих воздействий скорости конвейера. Результаты моделирования системы стабилизации скорости ленты конвейера подтверждают сделанные выводы. Результаты статьи могут найти применение для настройки параметров автоматических регуляторов систем управления транспортировкой руды дробильного агрегата, шаровой мельницы с целью повышения производительности на горно-обогатительных комбинатах.

В работе предлагается для подавления возмущающих воздействий гармонического вида, приложенных к выходу системы стабилизации скорости ленточного конвейера, использовать регулятор с встроенной моделью, представляющий объединение ПИ регулятора и дополнительной составляющей с встроенной моделью возмущающего воздействия. Подобный обобщенный регулятор позволяет обеспечить в системе нулевую ошибку в установившемся режиме при отработке гармонического возмущающего воздействия усредненной частоты, модель которой встраивается в регулятор. Показано, что для гармоник с частотами, отличающимися от осредненной частоты, имеет место достаточно хорошее подавление возмущающих воздействий. Для трехкратного изменения значения усредненной частоты подавление возмущения в примере происходит не хуже, чем в 300 раз. Так же с помощью моделирования можно устанавливать диапазон частот, где выполняется заданное ограничение на амплитуду установившегося значения ошибки. На основе типовых методов синтеза регуляторов предложена процедура определения значений настроечных параметров обобщенного регулятора.