OPTIMIZATION OF THE SCREEN LAYOUT FOR ONE-FINGER TYPING

В настоящее время все больший объем текста набирается на мобильных сенсорных устройствах – экранах смартфонов и планшетов. Такой набор обычно происходит в пути или другой нерабочей обстановке, где нет возможности обратиться к полноценному устройству для ввода текста – полноразмерной клавиатуре. В частности, таким образом, пишутся сообщения на различных форумах, краткие и развернутые ответы в мессенджерах и т.п., а иногда даже программный код.

Несмотря на различные альтернативные технологии ввода текста (Swype, MessageEase, KeyMonk и другие, включая голосовой и рукописный ввод), в случае нестандартных или нераспространенных слов, использования жаргонизмов, наиболее удобным вариантом остается посимвольный ввод текста. Этот метод является наименее ошибочным, требует минимального числа правок в процессе редактирования текста после ввода, что выгодным образом сказывается на производительности.

Разумеется, посимвольный ввод текста не отменяет различные надстройки, таких как предложение вариантов вводимого слова и предсказание следующего слова словосочетания, он может быть использован совместно с альтернативными технологиями ввода текста.

В данной работе будет рассматриваться оптимизация экранной раскладки для случая посимвольного набора одним пальцем. Такой набор производится в случае небольшого размера устройства, таких как смартфон, когда одной рукой набирать удобнее, чем двумя, или в случае, когда нет возможности задействовать вторую руку (например, во время поездки, стоя в общественном транспорте).

Для выполнения оптимизации экранной раскладки необходимо составить математическую модель и алгоритм оптимизации. Действиями, которые необходимо выполнить для решения поставленной задачи являются:

1) определение какие комбинация клавиш являются «хорошими» и «плохими»;

2) выбор компромисса между удобством и скоростью набора текста;

3) правильное распределение нагрузки на палец.

Во всех этих критериях обнаруживается субъективизм, но есть и утверждения, принимаемые исследователями как истинные, подтвержденные при помощи различных программ. Необходимо собрать все возможные случаи, проанализировать их и расставить по порядку предпочтительности.

Далее необходимо выбрать численные оценки качества, для этого каждой комбинации клавиш назначается некоторое усилие в баллах и здесь появляется субъективизм: первый субъективный выбор – какие комбинации клавиш хорошие, а какие плохие? Второй субъективный выбор – насколько лучше или хуже та или иная комбинация?

Есть один объективный критерий – расстояние, проходимое пальцами от исходной позиции. Необходимо учитывать, что нажатие каждой клавиши происходит не всегда из исходной позиции. Например: комбинация «ЗТ» — палец движется к верхнему ряду, а потом к нижнему, следовательно расстояние, проходимое до «Т» больше, чем из исходной позиции. Многие модели оптимизации минимизируют именно расстояние, но это не единственный критерий улучшения качества раскладки. Основная часть работы приходится не на горизонтальные и вертикальные перемещения пальца, а на нажатия клавиш. Поэтому основной путь совершенствования раскладки – минимизация доли неудобных комбинаций букв при наборе текста.

Затраты на нажатие каждой клавиши будут складываться из двух составляющих: на перемещение пальца и на нажатие клавиши, путем задания коэффициентов затрат на одно нажатие и единицу перемещения. Далее необходимо разработать систему поощрения хороших (быстрых и удобных) комбинаций и штрафования плохих. В результате получается математическая модель затрат при наборе текста, для того чтобы оценить качество раскладки по выбранной модели, нужно протестировать раскладку на каком-либо тексте.

При выборе объектов тестирования, необходимо учитывать, что выборка текстов должна хорошо отражать статистическую структуру русского языка и включать:

1) достаточный объем (от нескольких мегабайт);

2) разные жанры (проза, фантастика, научные тексты, публицистика), так как используются различные сочетания букв и их комбинации;

3) возможно, даже разные эпохи (классика, современность).

Далее этот текст обрабатывается по модели оценки качества раскладки, и определяется число баллов. Раскладка с максимальным числом баллов – лучшая. Однако тестировать весь многомегабайтный текст, испытывая различные раскладки, занимает большую продолжительность времени, так как число испытываемых раскладок будет исчисляться миллионами.

Для решения данной проблемы необходимо провести статистический анализ выборки и составить таблицу статистики n-грамм (n-символьных комбинаций, n – желаемая глубина анализа). В этом случае уже не обязательно проверять весь текст, а достаточно воспользоваться таблицей статистики, которая на порядки меньше по объему, чем исходные тексты. Затраты на набор каждой комбинации умножаются на число повторений в тексте этой комбинации.

Отметим, что прямым перебором выбрать квазиоптимальную раскладку невозможно, так как их число составляет 10 в 64 степени вариаций, учитывая только перестановки букв. В таком случае необходимо использовать приближенные методы оптимизации, которые называются методами эвристического поиска или случайной/псевдослучайной оптимизации. Основными из них являются:

1) базовый метод без модификаций - метод Монте-Карло;

2) метод имитации отжига;

3) генетический метод.

В данном исследовании было принято решение использовать метод отжига.

При запуске процесса оптимизации были собраны исходные данные о диграммах, которые включали в себя все двухсимвольные комбинации, определенные на основе анализа 300 Мб русскоязычного текста, при этом все заглавные буквы в статистике были преобразованы в строчные, а повторяющиеся диграммы сгруппированы. Была задана раскладка, от которой будет стартовать процедура оптимизации. Данная раскладка может быть как любой из существующих, так и сгенерированной случайно. В данном случае стартовой раскладкой является раскладка ЙЦУКЕН.

Шаг оптимизации выбирается при этом равным одной перестановке клавиш. Выбор большего шага может привести к тому, что решение не окажется достаточно близким к минимуму целевой функции. С другой стороны, малый шаг уменьшит скорость сходимости. Исходя из вышеперечисленного было решено, что в данном случае одна перестановка клавиш – подходящий шаг.

Для получения обоснованного результата процедуру оптимизации необходимо выполнить множество раз, а потом выбрать из полученных результатов лучшие. Это связано с тем, что процесс оптимизации является стохастическим и в большинстве случаев будет приводить к новому результату. Количество итераций для одной процедуры оптимизации выбирались равными 10000, 50000, 100000. Как показали вычисления, приемлемые результаты при допустимых временных затратах обеспечивает число итераций 10000, если выбирать из данного ряда.

Для оценки качества раскладки не только по модели усилий строится процедура, определяющая следующие характеристики:

1) доля клавиш основного ряда при наборе;

2) доля диграмм, набираемых в обратном порядке;

3) доля диграмм с согласованными перемещениями.

Также определяется распределение нагрузки по нажатиям и по перемещениям для пальца. На основании этих данных можно сделать более обоснованное заключение о качестве раскладки.

Исходя из вышесказанного, процесс оптимизация включает в себя следующие этапы:

1) загрузка исходного файла со статистикой диграмм, подготовка массива (чистка, преобразование прописных букв в строчные, группировка);

2) определение матрицы зон для каждого символа;

3) определение матрицы расстояний для зон в относительных единицах;

4) назначение двух матриц со штрафами на перемещение и на нажатие клавиши;

5) назначение величин дополнительных бонусов и штрафов для различных типов диграмм;

6) назначение стартовой раскладки, выбор шага оптимизации, выбор числа итераций;

7) оптимизация по методу отжига (многократная);

8) выбор наилучших раскладок;

9) расчет дополнительных характеристик существующих русскоязычных раскладок и оптимизированной раскладки.

Оптимизация раскладки для однопальцевого набора подразумевает составление некоторых критериев оптимизации – системы штрафов, которые будут влиять на сокращение суммарного пути, проходимого пальцем/пальцами между буквами при наборе среднестатистического текста. А расстояние, проходимое пальцем в горизонтальном направлении (плоскости экрана) от буквы к букве при наборе слова, равнозначно сумме расстояний между буквами всех диграмм – двухбуквенных составных частей слова. Например, набор слова «буква» равнозначен по расстоянию набору диграмм «бу», «ук», «кв», «ва» (без учета пробела).

Таким образом, исходный текст «заменяется» статистикой диграмм, по которой и будет составляться суммарное расстояние, проходимое пальцем. Причем в данном случае данная «замена» абсолютно правомерна и не приводит даже к малейшему снижению точности. Переход к статистикам различной глубины вместо исходного текста – это вынужденная мера с целью сократить время расчета штрафной функции (на порядки).

В первом приближении оптимизация экранной раскладки сводится к минимизации расстояний по статистике диграмм русского языка. В дальнейшем, в более детальной оптимизации, можно учесть, что направление сгибания-разгибания большого пальца менее удобное, чем перпендикулярное ему (латеральное).

Необходимо отметить, что стандартная раскладка ЙЦУКЕН, а точнее, ее экранная копия, должна быть достаточно близка к оптимальной для набора одной рукой или одним пальцем: все наиболее частые буквы, которые запоминаются при помощи слова «СЕНОВАЛИТР», находятся достаточно близко к середине раскладки,исключение составляют только буквы К, М, П, Г, Ь (2,5%, 2,5%, 2,1%, 1,4%, 1,6% соответственно). Результаты распределения нагрузки по пальцам представлены на рисунке 1.

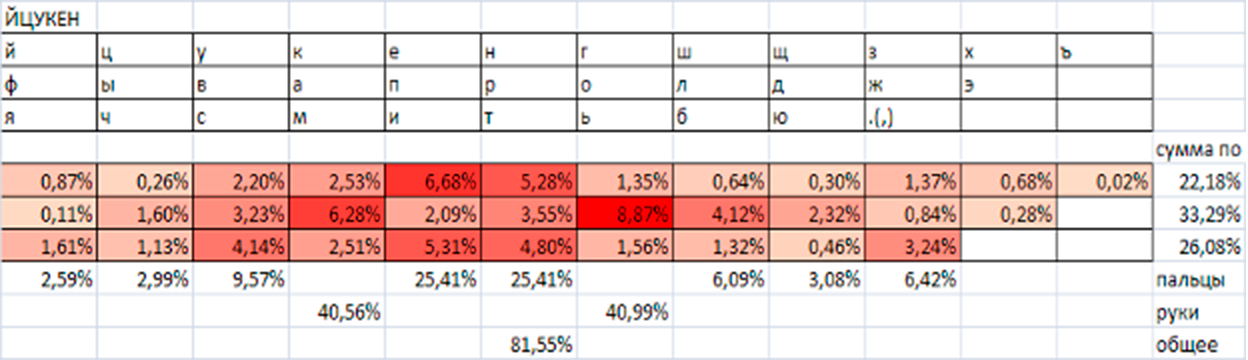
Рисунок 1 - Распределение нагрузки для раскладки ЙЦУКЕН

DOI:10.23670/IRJ.2023.138.124.1

Для расчета оптимальной клавиатурной раскладки знаки «.» и «,» (точка и запятая) разносились на разные клавиши, так как частота этих знаков существенна (приблизительно по 1,5¸1,6%). 

Необходимо учесть, что расстояние, проходимое пальцем на 1 набранный символ для неоптимизированной экранной раскладки ЙЦУКЕН по имеющейся статистике диграмм составило 3,039 стороны клавиши. Это является достаточно высоким показателем.

Оптимизация проводилась в различных вариациях, каждый из случаев будет рассмотрен отдельно.

В первом варианте геометрия экранной раскладки принималась такой же, как и для клавиатурной, за исключением горизонтального смещения между рядами. Клавиши различных рядов образуют строгую вертикаль в плоскости раскладки (рисунок 2б), а не расположены по диагоналям (рисунок 2а).

Рисунок 2 - Различное относительное расположение рядов: 

а - фрагмент клавиатуры Gigabyte K-7100; б - фрагмент клавиатуры TypeMatrix 2030

DOI:10.23670/IRJ.2023.138.124.2

Клавиша пробела принималась равной по размеру остальным клавишам, с положением на одной вертикали с цифрой «6», и не подвергалась перемещениям в процессе оптимизации, а также не участвовала в процессе расчета штрафа. Также оставались на месте и клавиши цифрового ряда. В процессе оптимизации изменялись только положения буквенных клавиш, а также точки и запятой.

Результат оптимизации приведен на рисунке 3. Свободные поля в данном случае также принимались запрещенными и не участвовали в оптимизации.

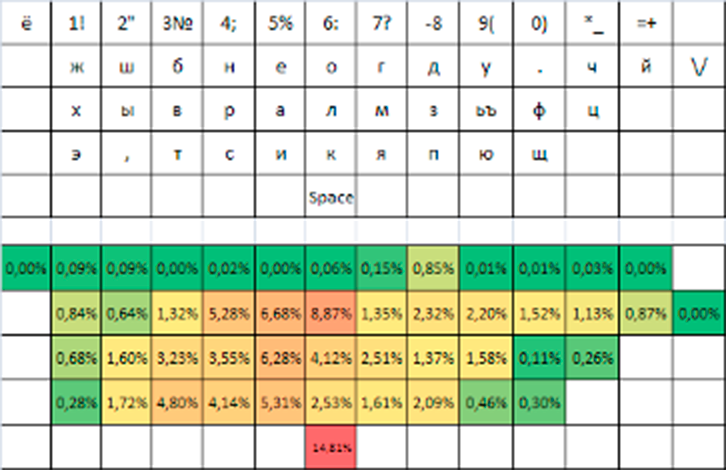
Рисунок 3 - Экранная раскладка, оптимизированная на стандартном поле 5х14

DOI:10.23670/IRJ.2023.138.124.3

Расстояние, проходимое пальцем при наборе, составило 93,8% от аналогичной величины стандартной раскладки ЙЦУКЕН, что не является значимым сокращением – разница составила 6,2%. Данный результат был получен ввиду того, что поле оптимизации было заранее ограничено 5х14 клеток и было невозможно формирование соответствующей квазиоптимальной структуры раскладки. Также необходимо учитывать, что пробелы составляют 14-15% от общего числа символов, соответственно, его также необходимо перемещать в процессе оптимизации для достижения хорошего результата.

Далее поле оптимизации было расширено до 7х14 клеток, кроме того, перемещались все клавиши, включая пробел. Появилась возможность разнести буквы «ь» и «ъ» на разные виртуальные клавиши, чтобы не требовалось дополнительное нажатие для активации второго слоя символов. Таким образом, все буквы и основные знаки находятся на разных местах первого (основного) слоя, то есть набираются в одно нажатие, без модификаторов. Число циклов оптимизации выбрано равным 10000.

Исходная раскладка ЙЦУКЕН и результат оптимизации с относительной частотой нажатий приведены на рисунках 4 и 5 соответственно.

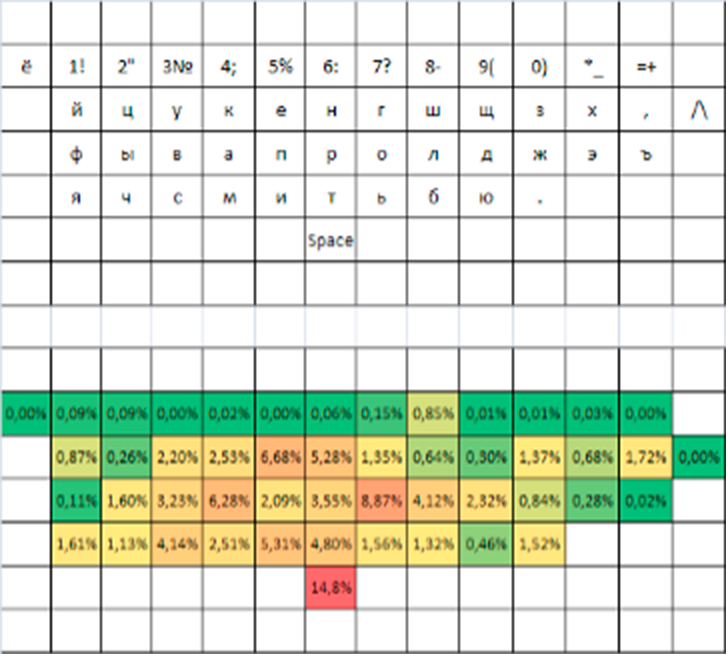
Рисунок 4 - Исходная экранная раскладка

DOI:10.23670/IRJ.2023.138.124.4

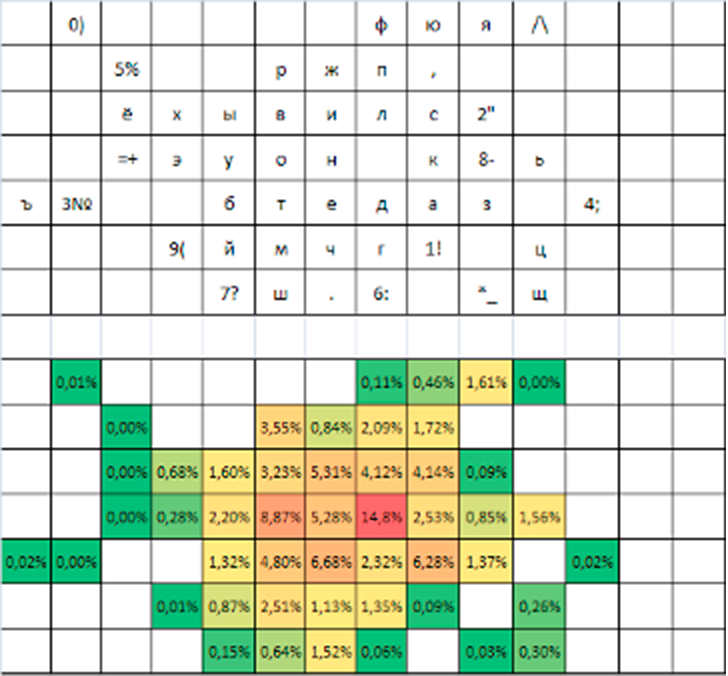
Рисунок 5 - Экранная раскладка, оптимизированная на поле 7х14

Примечание: 10000 циклов

DOI:10.23670/IRJ.2023.138.124.5

Проанализировав рисунок 5, выделяется стохастичность процесса оптимизации: символы перемещаются по всему доступному полю случайным образом, и каждая промежуточная раскладка, полученная на некоторой итерации, принимается или не принимается в соответствии с заданными критериями.

Результат такой стохастической оптимизации с большой вероятностью будет обладать некоторыми искажениями в области наименее важных позиций, поскольку они не оказывают большого влияния на штрафную функцию в целом. В данном случае такими позициями являются клавиши со статистически редкими символами, обозначенные темно-зеленым цветом, распределённые по краям основного кластера наиболее частотных символов.

Соответственно, для придания эстетичного вида такие раскладки нуждаются в небольшой ручной доработке, которая не окажет существенного влияния в сторону снижения эффективности, так как частота перемещаемых символов весьма мала. Возможно, что эффективность даже немного увеличится, потому что, например, периферийные перемещаемые буквы/знаки передвигаются только ближе ко всем без исключения остальным буквам/знакам. Например, в данном случае, это символы «ъ» и «4;», которые сразу можно сместить, соответственно, на 2 и 1 позицию ближе к центру по горизонтали. Для остальных случаев необходимо рассмотреть, какие сочетания с данной буквой наиболее частотные, и, соответственно, приближать её к основному кластеру в нужном направлении.

Данная раскладка обеспечивает уменьшение пути, проходимого пальцем при наборе, до 76,1% от аналогичной величины для исходной раскладки. Таким образом, улучшение составляет 23,9%, что является существенным показателем. Данный результат был получен вследствие расширения поля оптимизации и снятия ограничений на перемещение для всех клавиш.

На следующем этапе число циклов оптимизации увеличено до 50000. Необходимо отметить, что увеличение числа циклов не гарантирует улучшение результата, компромисс находится между скоростью выполнения оптимизации и её качеством.

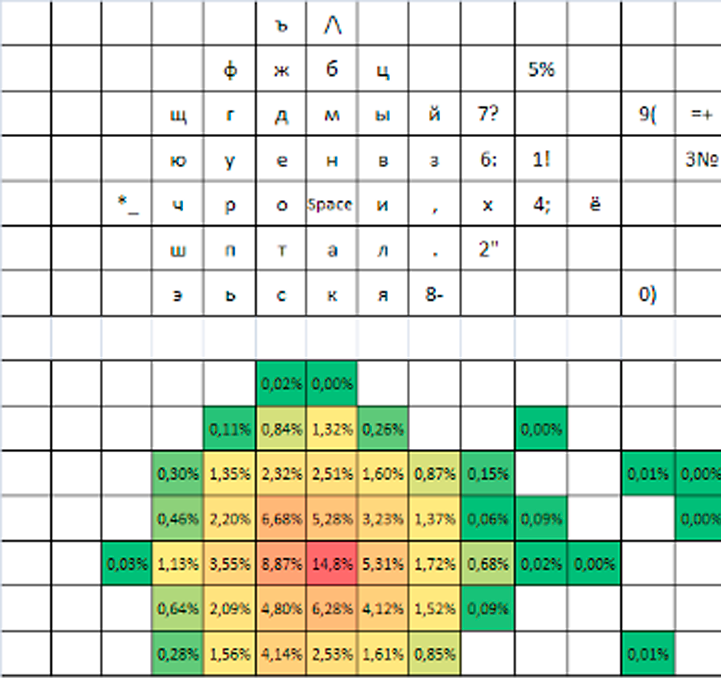
Рисунок 6 - Экранная раскладка, оптимизированная на поле 7х14

Примечание: 50000 циклов

DOI:10.23670/IRJ.2023.138.124.6

Стартовая раскладка выбиралась такой же, как и в предыдущем случае – ЙЦУКЕН. Как уже упоминалось, расстояние на 1 набираемый символ в среднем равно 3,039 размера клавиши. Проходимое расстояние в этом случае уменьшилось уже до 67,5% относительно первоначального, что является ещё лучшим результатом. График процесса оптимизации по методу имитации отжига приведен на рисунке 7.

Рисунок 7 - График процесса оптимизации для 50000 циклов

DOI:10.23670/IRJ.2023.138.124.7

Синим цветом показаны штрафы (средние расстояния на 1 символ) пробных, но не принятых раскладок, а красным – штрафы принятых. Розовой пунктирной линией показан штраф исходной раскладки – 3,039. В начале оптимизации раскладка сильно ухудшается, в 2 и более раз, так как на начальном этапе вероятность принятия плохих раскладок, которые являются хуже исходной велика. Далее, спустя приблизительно 1/3 от общего числа циклов качество раскладки приближается к исходному. Вероятность принятия плохих раскладок сильно уменьшается, тем самым, имитируется постепенное «охлаждение» объекта, с чем и связан термин «имитация отжига». В этой средней части происходит основное улучшение раскладки по отношению к первоначальной. Далее, в заключительной части процесса оптимизации, приблизительно с 35000-го цикла, значительных изменений раскладки не происходит, так как почти все пробные изменения приводят к ее ухудшению, а вероятность принятия плохих раскладок все время падает.

Итоговый результат: среднее расстояние, проходимое пальцем, при наборе 1 символа, составляет 2,052 клавиши. При сравнении данного результата с предыдущими можно сделать вывод, что данный результат является высоким качеством оптимизации, и дальнейшего существенного улучшения раскладки при увеличении числа циклов оптимизации ожидать маловероятно.

Для подтверждения корректности предположений, было решено провести еще один дополнительный этап оптимизации, использовав другие стартовые условия. Во-первых, изменена конфигурация поля оптимизации с 7х14 на 9´9 для того, чтобы обеспечить более эффективное перемещение символов и обеспечить возможный больший диаметр основного кластера для наиболее частотных из них. Во-вторых, исходная раскладка была приближена к оптимальной вручную следующим способом: на центральную клетку поля помещался самый частотный символ – пробел, на соседнюю клетку выше помещалась буква «о», второй символ по частоте, а далее заполнение символами шло почасовой стрелке в порядке убывания их частоты. В-третьих, число циклов оптимизации увеличено вдвое по сравнению с предыдущим случаем и равно 100000. Таким способом решено проверить, как влияет стартовая раскладка и дальнейшее увеличение числа циклов на результат оптимизации. В результате была получена квадратная раскладка (рис 8). Необходимо отметить, что среднее расстояние на 1 символ для нее равен 2,271, что уже составляет 74,7% от первоначальной величины (ЙЦУКЕН) до проведения оптимизации.

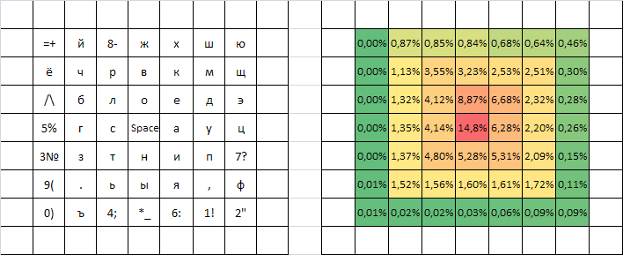
Рисунок 8 - Исходная раскладка для оптимизации на поле 9х9

DOI:10.23670/IRJ.2023.138.124.8

Результат оптимизации и график процесса оптимизации представлены на рисунках 9 и 10 соответственно.

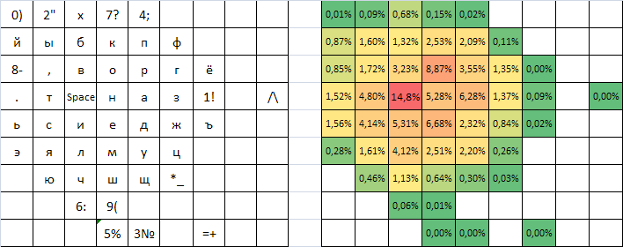
Рисунок 9 - Экранная раскладка, оптимизированная на поле 9х9

Примечание: 100000 циклов

DOI:10.23670/IRJ.2023.138.124.9

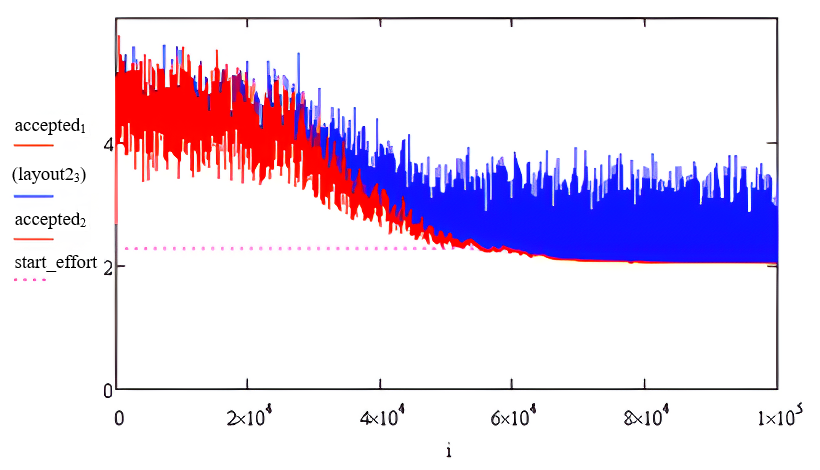
Рисунок 10 - График процесса оптимизации для 100000 циклов

DOI:10.23670/IRJ.2023.138.124.10

Анализируя рисунок 10, отметим, что значительного визуального отличия формы графика от аналогичного процесса для 50000 циклов нет. Вместе с тем, видно, что штраф начальной раскладки составляет 2,271, данная величина сразу ухудшается в 2 раза, но снижается ниже первоначальной величины во второй половине процесса оптимизации. Итоговое значение равно 2,046, что является лучшим на 0,5% результата оптимизации для 50000 циклов. Можно сделать вывод о том, что увеличение числа циклов выше 50000 для рассматриваемого случая не дает существенного увеличения качества раскладки и является нецелесообразным.

Вручную отредактировав крайнюю оптимизированную раскладку, был получен законченный ее вариант, который представлен на рисунке 11.

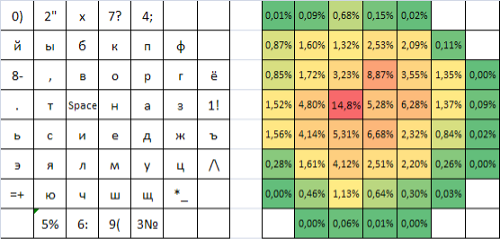
Рисунок 11 - Раскладка, полученная в результате редактирования

DOI:10.23670/IRJ.2023.138.124.11

В заключении можно отметить, что оптимизация раскладки для однопальцевого набора имеет важное значение для повышения эффективности и удобства набора текста. Составление критериев оптимизации, основанных на статистике диграмм русского языка, позволяет сократить суммарный путь, проходимый пальцем между буквами при наборе текста.

При помощи оптимизации можно добиться значительного уменьшения проходимого расстояния до 76,1% от исходной раскладки, что является существенным улучшением. Стоит отметить, что стохастический характер процесса оптимизации требует ручной доработки, особенно для редко используемых символов, чтобы придать раскладке эстетичный вид.

Полученные результаты оптимизации подтверждают целесообразность использования оптимальных раскладок для однопальцевого набора, обеспечивающих повышенную эффективность и комфорт при наборе текста. При дальнейшем исследовании можно учесть и другие факторы, такие как направление сгибания-разгибания большого пальца, для достижения ещё более оптимальных результатов.

Таким образом, оптимизация раскладки для однопальцевого набора является важным направлением исследований, которое способствует повышению эффективности набора текста, и может быть использовано для разработки более удобных и оптимальных клавиатурных раскладок.