MATHEMATICAL MODELING OF STRUCTURE FORMATION OF COMPOSITE MATERIALS USING DYNAMIC MODELS

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ СТРУКТУРООБРАЗОВАНИЯ КОМПОЗИЦИОННЫХ МАТЕРИАЛОВ ПРИ ПОМОЩИ ДИНАМИЧЕСКИХ МОДЕЛЕЙ

Научная статья

Бормотов А.Н.^1, *, Горохова А.А.²

¹ ORCID: 0000-0001-7069-6603;

¹ Пензенский государственный технологический университет, Пенза, Россия;

² Пензенский государственный университет архитектуры и строительства, Пенза, Россия

* Корреспондирующий автор (aleks21618[at]yandex.ru)

Аннотация

Предложен математический метод моделирования процессов структурообразования дисперсных систем и композиционных материалов, в частности, при помощи динамических моделей, учитывающих энергетические, структурные и реологические особенности межчастичного взаимодействия. Рассмотрены условия протекания процессов самопроизвольного образования флокул и кластеров. Построены математические модели структурообразования кластеров в дисперсных системах, определены параметры кластеров и рецептурно-технологические условия их образования. На основе предложенных моделей и математических методов показана возможность управления процессами структурообразования дисперсных систем с целью получения оптимальных параметров структуры и свойств композиционных материалов.

Ключевые слова: композиционные материалы, математическое моделирование, структурообразование, дисперсные системы, оптимизация свойств.

MATHEMATICAL MODELING OF STRUCTURE FORMATION OF COMPOSITE MATERIALS USING DYNAMIC MODELS

Research article

Bormotov A.N.^1, *, Gorokhova A.A.²

ORCID: 0000-0001-7069-6603;

¹ Penza State Technological University, Penza, Russia;

² Penza State University of Architecture and Construction, Penza, Russia

* Corresponding author (aleks21618[at]yandex.ru)

Abstract

The study proposes a mathematical method for modeling the processes of structure formation of dispersions and composite materials through the use of dynamic models that take into account the energy, structural and rheological features of interparticle interaction. The article considers the conditions of the spontaneous formation of floccules and clusters. The research includes the construction of mathematical models of cluster structure formation in dispersions as well as defines the cluster parameters, and formulation and technological conditions for their formation. Based on the proposed models and mathematical methods, the study demonstrates the possibility of controlling the processes of structure formation of dispersions in order to obtain optimal parameters of the structure and properties of composite materials.

Keywords: composite materials, mathematical modeling, structure formation, dispersed systems, optimization of properties.

Введение

Композиционные материалы (КМ) по своей природе относятся к дисперсным системам, которые получаются соединением вязкой матрицы (вяжущее) и тонкомолотых дисперсных фаз различной природы (наполнители). Данное обстоятельство необходимо учитывать при математическом моделировании процессов структурообразования КМ. Именно такими системами и являются композиционные материалы со специальными или экстремальными свойствами. При использовании оптимальных рецептурно-технологических параметров получение изделий требует небольших энергетических затрат.

Структурообразование композитов, наполненных дисперсными минералами, определяется взаимодействиями между структурообразующими элементами – флокулами и кластерами, а также процессами, происходящими на поверхностях указанных конгломератов и в прослойках вяжущего. Толщина прослойки вяжущего и размеры дисперсных конгломератов оказывают определяющее влияние на реологические свойства композитов и на структуру и эксплуатационные свойства композиционных материалов [1], [2], [7]. Появление новых системных свойств у композитов как сложных технических систем связано с появлением новообразований – флокул (кластеров), что отличает композиты от механической смеси компонентов и является основным фактором качества моделирования структурообразования композитов [3]. Одной из важнейших научно-технических задач, имеющей большое практическое значение, является разработка методов математического моделирования механизма структурообразования (флокулообразования) с целью получения заданных структуры и свойств КМ. 

Методы и принципы исследования

Для того чтобы выполнить адекватное математическое моделирование процессов структурообразования композиционных материалов, необходимо иметь адекватное математическое описание физических и технологических параметров формирования структуры композитов в формализованном виде.

Получение математического описания процессов структурообразования композиционных материалов выполнялось аналитическим методом и методом компьютерного моделирования. В качестве аналитических методов применялись методы моделирования динамических и кинематических режимов флокулообразования. Для таких методов характерно наличие громоздкого математического аппарата. В тоже время данные методы могут использоваться для оценки адекватности результатов численного моделирования. Достоинством аналитических методов является возможность математического и имитационного моделирования процессов флокулообразования, в значительной степени определяющего эксплуатационные свойства композиционного материала [4].

При моделировании структурообразования дисперсных наполненных систем использовались методы системного анализа и теории оптимального управления на основе аналитического, реологического, энергетического, структурного, кибернетического и информационного подходов. Для моделирования множества сочетаний структурообразующих факторов применялась авторская методика совместного решения аналитических зависимостей взаимодействий структурообразующих элементов и численного компьютерного моделирования математического описания условий флокулообразования.

Основные результаты

Как известно, эволюция структурообразования дисперсных систем определяется межфазными взаимодействиями между структурообразующими элементами [5]. В наполненном дисперсными минералами композите одной из базовых структурных единиц является самопроизвольно возникающий флокулярный или кластерный конгломерат.

В работе предлагается математическое описание наполненных композитов, процессы структурообразования которых можно описать системой уравнений:

    (1)

где m_i - масса i-й частицы;   - радиус-вектор координат i-й частицы; N – количество частиц наполнителя; k - коэффициент, определяемый диссипативными свойствами дисперсного наполнителя, v_i - скорость дисперсионной среды в точке r_i; U_i - энергетический потенциал в точке r_i, в общем случае зависящий от параметров дисперсионной среды и от взаимного расположения всех остальных частиц системы.

Левая часть уравнения (1), являющаяся разностью сил инерции и вязкого трения, неизменна по форме для любой дисперсной системы. Выражение для градиента в правой части (1) оказывается сложным и неоднозначным для каждого отдельного случая.

Потенциал межчастичного взаимодействия в уравнении (1) включает множество слагаемых, однако вклад в общий результат большинства из них на один-два порядка меньше вклада первых двух [6]. Примем бинарный потенциал для системы с единственным положением равновесия в виде:

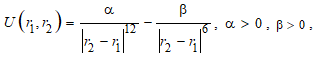     (2)

Выражение (2) содержит два независимых параметра, численные значения которых зависят от следующих параметров (рисунок 1):

• расстояния 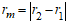, соответствующего координате равновесия, для которого характерно ;
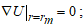• величины потенциальной ямы 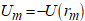, отсчитываемой от нулевого уровня энергии.

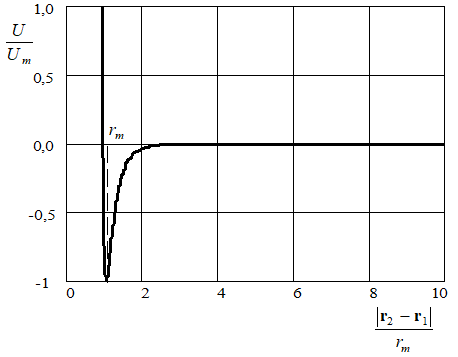
Рис. 1 – Принятый бинарный потенциал взаимодействия частиц

 

Значения параметров в уравнении (2) связаны с указанными величинами следующими соотношениями:

      (3)

Физико-механические свойства связующего – матрицы, полученной совмещением минеральных или органических вяжущих веществ с тонкомолотыми наполнителями – зависят от формирования их оптимальной структуры. Повышение макросвойств матрицы вяжущего зависит от параметров структуры вяжущего, от вида и скорости поверхностных явлений на границе раздела фаз, а также от количества наполнителя v_f, его дисперсности S_уд и физико-химической активности поверхности наполнителей и заполнителей. Для лиофильных систем оптимизация наполнения КМ может осуществляться изменением v_f и S_уд, соотношение которых позволяет рассчитать усредненную толщину прослойки вяжущего между частицами наполнителя h. Достижение рассчитанной толщины прослойки вяжущего зависит от длительности процесса диспергирования, а поверхностными явлениями не определяется [7]:

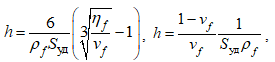       (4)

Где ρ_f, S_уд, v_f – плотность, удельная поверхность, объемная доля материала наполнителя соответственно; h_f – максимальная плотность упаковки частиц.

Как показывают исследования, граничный или сольватный слой вяжущего вещества образуется при совмещении компонентов связующего на границе раздела фаз. Этот слой характеризуется плотным и упорядоченным расположением структурных элементов вяжущего и крупных молекул олигомера. Реологические свойства смесей и физико-механические свойства КМ зависят от толщины сольватного слоя, от строения слоя и прочности сцепления сольватной оболочки с поверхностью частиц дисперсной фазы. Однако граничный слой определяет еще и агрегативную устойчивость дисперсионной системы, от которой зависит возможность образования в структуре композита кластеров. Как показывают исследования авторов, если толщина прослойки вяжущего многократно превосходит толщину сольватной оболочки, то самопроизвольное образование кластеров невозможно из-за ничтожно малого влияния поверхностной энергии частиц дисперсной фазы.

Определение толщины сольватной оболочки предлагается выполнять на основе реологического, энергетического, структурного подходов.

Реологический подход основан на законе Эйнштейна:

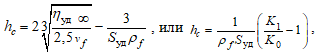     (5)

где  – приведенная вязкость; K₁ , K₀ – коэффициенты, определяемые по вязкостям дисперсной системы, в которой среда не образует совсем или образует на поверхности частиц сольватную оболочку бесконечно малой толщины.

Энергетический подход заключается в учете Ван-дер-Ваальсовского взаимодействия молекул:

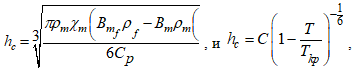      (6)

где ; ρ_m – плотность вяжущего вещества; ρ_m – плотность вяжущего при толщине h; χ_m – изотермическая сжимаемость вяжущего; B_m и B_mf – константы Ван-дер-Ваальсовского взаимодействия молекул, вяжущего между собой и структурными элементами другой фазы соответственно; T_кр – критическая температура структурообразования.

Структурный подход основан на учете процессов, протекающих на границе раздела фаз:

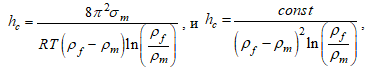     (7)

где σ_m – поверхностное натяжение вяжущего вещества.

Из (5)...(7) следует, что при заметном удалении от T_кр значения h_c находятся в интервале 10^-7...10^-9 м. Причем для веществ, состоящих из сложных молекул, толщина h_c близка к 10^-7...10^-8 м; для веществ, состоящих из простых молекул, – близка к 10^-9.

Как показывает практика, использование формул (5)...(7) сопряжено с трудностями инструментального определения величин. Процессы, протекающие на границе раздела фаз, невозможно оценить.

Авторами предлагается способ определения h_c, лишенный указанных недостатков. Он основан на энергетическом подходе. А именно, при смачивании поверхности твердого тела выделяется энергия, равная:

      (8)

где σ_ж – поверхностное натяжение; θ – краевой угол смачивания поверхности твердого тела; S – площадь смоченной поверхности. Эта энергия расходуется на образование сольватного слоя с числом молекул , где N_A – постоянная Авогадро; RT – тепловая энергия 1 моля вяжущего.

Толщина и масса сольватного слоя определяются в виде:

    (9) где m_c , ρ_c – масса и плотность слоя соответственно, M – молекулярная масса вяжущего.

Соотношения (8) и (10) определяют коэффициенты в выражении для потенциала. Из (7), (8) и (9), получим:

    (10)

Из (10) получаем, что толщина прослойки вяжущего возрастает с увеличением молекулярной массы, размеров молекул, поверхностного натяжения вяжущего. Также на увеличение толщины сольватного слоя влияет увеличение смачиваемости поверхности наполнителя вяжущим. Уменьшение толщины прослойки вяжущего наблюдается при повышении температуры и плотности слоя. Данные положения подтверждаются экспериментальными данными [8], [9].

При предварительных расчетах можно принять . Максимальная толщина сольватного слоя тогда определится по (10):

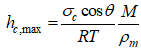     (11)

Значения толщина сольватного слоя для некоторых вяжущих веществ приведены в таблице 1.

 

Таблица 1 – Максимальная толщина сольватного слоя h_c,max, нм [8]

Вид вяжущего	Температура, 0С
	25	50	75	125	150
Серное вяжущее	–	–	–	2,12	2,02
Эпоксидная фенол-альдегидная смола	14,6	13,4	12,5	–	–
Фенолформальдегидная смола	13,4	12,4	11,5	–	–

 

Расчетные значения h_c,max совпадают с экспериментальными данными, и формула (11) может быть использована для исследования процессов структурообразования (флокулообразования) КМ [8], [9].

Для теоретической системы из двух частиц при отсутствии внешних сил, с учетом их значительного удаления друг от друга (, в выражении (1) для потенциала значимым является второе слагаемое; первое – может быть отброшено.

Моделирование структурообразования проводили с прямоугольной системой координат. Начало координат располагалось в месте первой частицы, а направление оси абсцисс выбиралось по направлению вектора . При малом трении уравнение (2) запишем в виде:

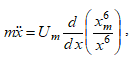     (12)

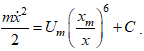где Um – глубина потенциальной ямы ,  – ее положение. Далее:     (13)

За начало отсчета принимаем момент соприкосновения частиц, направление отсчета меняем на противоположное. Тогда постоянная интегрирования  (целесообразность задания начального условия в такой форме будет обоснована ниже) и

     (14)

Как видно, с ростом времени t обе части (14) возрастают (потенциальная энергия взаимодействия частиц переходит в кинетическую), расстояние x между частицами – уменьшается.

Из (14) имеем:

      (15)

Следовательно, время «самопроизвольного» образования флокул в КМ (время перемещения частицы из точки  определится в виде:

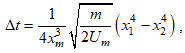      (16)

которое быстро увеличивается вместе с увеличением начального расстояния между частицами (пропорционально четвертой степени расстояния).

Расчетные значения Δt, полученные в соответствии с (16) для частиц диаметром 1 мкм, приведены в таблице 2. Принималось:  – определяемая по (4) максимальная толщина сольватного слоя, N – число молекул в сольватном слое, k – постоянная Больцмана, T – температура.

 

Таблица 2 – Оценка времени кластерообразования, лет

Вид вяжущего	Начальное расстояние между частицами, мкм
	1	5	10	50	100
Серное вяжущее	1	500	10000	5×106	108
Эпоксидная смола	3 сут.	5	100	5×104	106

 

Приведенные значения в таблице 2 являются нижним пределом времени кластерообразования (без учета сил отталкивания и диссипативных свойств системы). Точные экспериментальные значения будут больше, чем приведенные в таблице 2.

Покажем возможность образования линейного кластера за счет захвата частиц в процессе перемешивания композиции. Система координат выбираем так, чтобы в правой части осталось единственное ненулевое слагаемое. Пренебрегая силами инерции, закон движения частицы можно представить в виде:

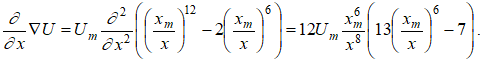      (17) где  – скорости частицы и дисперсионной среды соответственно. Точка, соответствующая максимальному значению силы  будет:      (18) Приравнивая производную к нулю, получим:      (19) Значение силы, действующей на частицу в точке :      (20)

Приравнивая силу вязкого трения, действующую на частицу со стороны дисперсионной среды, силе, действующей на частицу со стороны поля другой частицы, получим предельное значение скорости дисперсионной среды, при которой еще возможно кластерообразование:

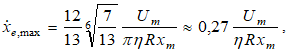     (21) где R – радиус частицы, η – вязкость среды.

Значения предельной скорости, рассчитанные в соответствии с (21), приведены в таблице 3.

 

Таблица 3 – Оценка предельная скорость дисперсионной среды, мм/с

Вид вяжущего	Диаметр частицы, мкм
	0,1	0,5	1	5	10
Серное вяжущее	1,3×106	2,6×105	1,3×105	2,6×104	1,3×104
Эпоксидная смола	1,7	0,34	0,17	0,03	0,02

  Заключение

Из представленных результатов следует, что образование кластеров в процессе перемешивания композиции за счет захвата частиц в высоковязких системах не происходит, т.к. силы вязкого трения, действующие на частицу со стороны дисперсионной среды, приводят к разрушению кластеров. Однако, образование кластеров в низковязких наполненных системах возможно при поступлении энергии извне – т.е. при различных способах энергетической накачки системы – интенсивном перемешивании, подогреве, встряхивании, обработке ультразвуком и пр.

Анализ результатов позволяет сделать вывод, что самопроизвольное образование флокул из макроскопических (более 1 мкм) частиц также невозможно. В системах, состоящих из частиц, линейные размеры которых, а также межчастичное расстояние между которыми, сопоставимы с величиной h_c,max – возможно образование флокул и флокулярных конгломератов.

Уравнение (16) является одной из компонент обобщенной модели структурообразования дисперснонаполненных систем [7] и позволяет оценить время «самопроизвольного» образования флокул в композиционном материале при управляемом многокритериальном синтеза композитов с заданными параметрами структуры.

Разработанный метод имитационного моделирования флокулообразования в дисперсных системах позволяет учесть влияния основных рецептурных и технологических факторов на процесс структурообразования композитов. Адекватность полученных аналитических решений подтверждается численными решениями, полученными для известных композиционных материалов с погрешностью не выше 5% [8], [10].

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References

1. Эбелинг, В. Физика процессов эволюции / В. Эбелинг, А. Энгель, Р. Файстель. - М. : УРСС, 2001. - 326 с.
2. Бобрышев, А.Н. Синергетика композиционных материалов / А.Н. Бобрышев, В.Н. Козомазов, Л.О. Бабин, В.И. Соломатов - Липецк : НПО ОРИУС, 1994. - 152 с.
3. Бормотов, А.Н. Разработка и управление качеством строительных материалов с регулируемой структурой и свойствами для защиты от радиации / А.Н. Бормотов, А.П. Прошин, Е.В. Королев, А.М. Данилов, И.А. Гарькина // Идентификация систем и задачи управления SICPRO’03: Труды II Международной конференции. – М. : Институт проблем управления им. В.А. Трапезникова РАН, 2003. – С. 2437-2460.
4. Прошин, А.П. Динамические модели при исследовании кластерообразования в композиционных материалах. Предельные системы / А.П. Прошин, А.М. Данилов, Е.В. Королев, В.А. Смирнов // Известия вузов. Строительство. – №3. – 2003. – С. 32-38.
5. Прошин, А.П. Теоретические аспекты синтеза полимерных композиционных материалов для защиты от радиации / А.П. Прошин, А.М. Данилов, И.А. Гарькина, А.Н. Бормотов, В.И. Соломатов // Известия ВУЗов. Строительство и архитектура. – № 6. – 2001. – С. 7-9.
6. Мелькер, А.И. Самоорганизация и образование геликоидальных структур полимеров / А.И. Мелькер, Т.В. Воробьева // Физика твердого тела. - - Т. 39. - № 10. - С. 1883-1889.
7. Бормотов А.Н. Математическое моделирование и многокритериальный синтез композиционных материалов специального назначения : дис. … док. техн. наук : 05.13.18 : защищена 21.12.2011 : утв. 30.08.2012 / Бормотов Алексей Николаевич. – Пенза, Пензенский государственный технологический университет, 2011 – 316 с.
8. Бормотов А.Н. Полимерные композиционные материалы для защиты от радиации : монография. – М., Палеотип, 2012. – 272 с.
9. Proshin A.P. The Extra-Heavy Concrete For Protection From Radiation / P. Proshin, E.V. Korolev, A.N. Bormotov, O.L. Figovsky //Proceedings of the International Conference on Role of Concrete in Nuclear Facilities2005 International Congress – Global Construction: Ultimate Concrete Opportunities. Ser. "Role of Concrete in Nuclear Facilities – Proceedings of the International Conference". – University of Dundee, Concrete Technology Unit. Dundee, Scotland, 2005. – С. 69-76.
10. Бормотов А.Н. Математическое моделирование и многокритериальный синтез композиционных материалов / А.Н. Бормотов, И.А. Прошин, Е.В. Королев. – Пенза, Изд-во ПГТА, 2011. – 352 с.

Список литературы на английском языке / References in English

1. Ebeling, V. Fizika processov evolyucii [Physics of evolutionary processes] / V. Ebeling, A. Engel', R. Fajstel'. – M.: URSS, 2001. – 326 p. [in Russian]
2. Bobryshev, A.N. Sinergetika kompozicionnyh materialov [Synergetics of composite materials] / A.N. Bobryshev, V.N. Kozomazov, L.O. Babin, V.I. Solomatov – Lipeck : NPO ORIUS, 1994. – 152 p. [in Russian]
3. Bormotov, A.N. Razrabotka i upravlenie kachestvom stroitel'nyh materialov s reguliruemoj strukturoj i svojstvami dlya zashchity ot radiacii [Development and quality management of building materials with adjustable structure and properties for radiation protection] / A.N. Bormotov, A.P. Proshin, E.V. Korolev, A.M. Danilov, I.A. Gar'kina // Identifikaciya sistem i zadachi upravleniya SICPRO’03: Trudy II Mezhdunarodnoj konferencii [Identification of systems and control tasks SICPRO'03: Proceedings of the II International Conference]. – M. : Institut problem upravleniya im. V.A. Trapeznikova RAN [Institute of Management Problems. V.A. Trapeznikov RAS], 2003. – P. 2437-2460. [in Russian]
4. Proshin, A.P. Dinamicheskie modeli pri issledovanii klasteroobrazovaniya v kompozicionnyh materialah. Predel'nye sistemy [Dynamic models in the study of clustering in composite materials. Limiting systems] / A.P. Proshin, A.M. Danilov, E.V. Korolev, V.A. Smirnov // Izvestiya vuzov. Stroitel'stvo [Izvestiya vuzov. Building]. – №3. – 2003. – P. 32-38. [in Russian]
5. Proshin, A.P. Teoreticheskie aspekty sinteza polimernyh kompozicionnyh materialov dlya zashchity ot radiacii [Theoretical aspects of the synthesis of polymer composite materials for protection from radiation] / A.P. Proshin, A.M. Danilov, I.A. Gar'kina, A.N. Bormotov, V.I. Solomatov // Izvestiya VUZov. Stroitel'stvo i arhitektura [Proceedings of the universities. Construction and architecture]. – № 6. – 2001. – P. 7-9. [in Russian]
6. Mel'ker, A.I. Samoorganizaciya i obrazovanie gelikoidal'nyh struktur polimerov [Self-organization and formation of helicoidal structures of polymers] / A.I. Mel'ker, T.V. Vorob'eva // Fizika tverdogo tela [Solid State Physics]. – 1997. – Vol. 39. – № 10. – P. 1883-1889. [in Russian]
7. Bormotov A.N. Matematicheskoe modelirovanie i mnogokriterial'nyj sintez kompozicionnyh materialov special'nogo naznacheniya [Mathematical modeling and multicriteria synthesis of composite materials for special purposes] : dis. … of PhD in Engineering : 05.13.18 : defense of the thesis 21.12.2011 : approved 30.08.2012 / Bormotov Aleksej Nikolaevich [Bormotov Alexey Nikolaevich]. – Penza, Penzenskij gosudarstvennyj tekhnologicheskij universitet [Penza State Technological University], 2011 – 316 p. [in Russian]
8. Bormotov A.N. Polimernye kompozicionnye materialy dlya zashchity ot radiacii : monografiya [Polymeric composite materials for radiation protection: monograph]. – M., Paleotip [Paleotype], 2012. – 272 p. [in Russian]
9. Proshin A.P. The Extra-Heavy Concrete For Protection From Radiation / P. Proshin, E.V. Korolev, A.N. Bormotov, O.L. Figovsky //Proceedings of the International Conference on Role of Concrete in Nuclear Facilities2005 International Congress – Global Construction: Ultimate Concrete Opportunities. Ser. "Role of Concrete in Nuclear Facilities – Proceedings of the International Conference". – University of Dundee, Concrete Technology Unit. Dundee, Scotland, 2005. – С. 69-76. [in English]
10. Bormotov A.N. Matematicheskoe modelirovanie i mnogokriterial'nyj sintez kompozicionnyh materialov [Mathematical modeling and multicriteria synthesis of composite materials] / A.N. Bormotov, I.A. Proshin, E.V. Korolev. – Penza, Publishing house PSTA, 2011. – 352 p. [in Russian]