Submit manuscript Sign in / Sign up
Advanced search
Article sections

EMPIRICAL SIMULATION OF THE HARDNESS DISTRIBUTION OF AN α-SOLID SOLUTION OF A NITRIDED CASE

Research article
Krukovich M.G.
Fedotova A.D.
DOI:
https://doi.org/10.23670/IRJ.2020.102.12.007
Issue: № 12 (102), 2020
Published:
2020/12/17

ЭМПИРИЧЕСКОЕ МОДЕЛИРОВАНИЕ РАСПРЕДЕЛЕНИЯ ТВЕРДОСТИ α - ТВЕРДОГО РАСТВОРА АЗОТИРОВАННОГО СЛОЯ

Научная статья

Крукович М.Г.1, *, Федотова А.Д.2

1 ORCID: 0000-0001-5563-093Х;

1, 2 Российский университет транспорта (МИИТ), Москва, Россия

* Корреспондирующий автор (ya.bormag[at]yandex.ru)

Аннотация

На основании множества проведенных экспериментов азотирования в газовых, жидких и твердых средах различных конструкционных сталей установлено влияние легирующих элементов на кинетику роста фаз слоя и твердость. Разработана и апробирована эмпирическая модель предиктивного расчета распределения содержания азота и твердости по толщине α – твердого раствора азотированного слоя. Модель предусматривает применение термодинамического коэффициента активности азота и его зависимости от суммарного влияния содержания легирующих элементов. Представлены сравнительные результаты численных экспериментов расчета максимальной твердости и ее распределения по толщине α - слоя с реальными экспериментальными данными на различных сталях. Расчет по представленной модели показал более высокое совпадение с экспериментами, чем рекомендуемые в литературных источниках методики расчета.

Ключевые слова: азотированный слой, эмпирическая модель, твердость, α – фаза, легирующий элементы, конструкционная сталь, коэффициент термодинамической активности азота, предиктивный расчет.

EMPIRICAL SIMULATION OF THE HARDNESS DISTRIBUTION OF AN α-SOLID SOLUTION OF A NITRIDED CASE

Research article

Krukovich M.G.1, *, Fedotova A.D.2

1 ORCID: 0000-0001-5563-093X;

1, 2 Russian University of Transport (MIIT), Moscow, Russia

* Corresponding author (ya.bormag[at]yandex.ru)

Abstract

The study establishes the influence of alloying elements on the kinetics of layer phase growth and hardness based on numerous nitriding experiments in gas, liquid, and solid media of various types of structural steel. The article develops and tests an empirical model for predictive calculation of the distribution of nitrogen content and hardness over the depth of the α – solid solution of the nitrided case. The model provides for the application of the thermodynamic coefficient of nitrogen activity and its dependence on the total effect of the content of alloying elements. The research presents comparative results of numerical experiments for calculating the maximum hardness and its distribution over the depth of the α-layer with real experimental data on various types of steel. The calculation that is based on the presented model shows a higher agreement with the experiments than the calculation methods recommended in the literature.

Keywords: nitrided case, empirical model, hardness, α-phase, alloying elements, structural steel, coefficient of thermodynamic activity of nitrogen, predictive calculation.

Введение

Твердость нитридных фаз азотированного слоя, имеющих ограниченную толщину (0,01 – 0,04 мкм) в зависимости от условий обработки и материала подложки изменяется в достаточно узком интервале и составляет 1000 – 1300 HV [1], [3], [4]. В то же время она может значительно уменьшаться в зависимости от пористости поверхностного слоя. Основную часть азотированного слоя на конструкционных сталях составляет α-твердый раствор с дисперсными включениями нитридов, который и определяет основные эксплуатационные характеристики слоя, сжимающие напряжения на поверхности упрочненных деталей и плавное уменьшение твердости от поверхности к сердцевине детали.

Твердость диффузионной части азотированного слоя представляет собой сумму упрочнения твердого раствора (∆т.р.) и упрочнения дисперсными частицами (∆д.ч.). Следовательно, степень упрочнения определяется концентрацией азота в слое и геометрическими параметрами выделяющихся в матрице нитридных фаз. Упрочнение при формировании диффузионной зоны, является результатом торможения дислокаций включениями нитридов, поэтому для расчета целесообразно использовать модели Мотта - Набаppo и Орована. Теория Мотта н Набарро применима для случаев когерентного выделения частиц второй фазы. В этом случае при деформации частицы перерезаются движущейся дислокацией. Для матрицы с некогерентными частицами второй фазы различают три механизма дислокационного взаимодействия: для случая тонких выделений – механизм перерезания частиц, механизм огибания частиц (по Оровану) и механизм переползания (по Хиршу) [2], [5], [9].

Проведенные расчеты [10] показали, что максимальное упрочнение азотированного слоя можно получить как за счет когерентных, так и некогерентных выделений путем соответствующей оптимизации структуры при реализации расчетных показателей: диаметра выделений и дистанции между ними. В то же время расчет суммарной твердости азотированных легированных сталей по вышеупомянутой методике приводит к получению результатов с ошибкой ~ 15% [5].

Таким образом, целью данной работы является разработка эмпирической модели расчета твердости α – фазы азотированного слоя, обеспечивающей получение более достоверных результатов.

Сущность разработанной модели

Моделирование распределения твердости по толщине слоя α-твердого раствора конструкционных сталей в данной работе проводилось в два этапа. На первом этапе рассчитывалось влияние легирующих элементов (до 6 % по массе) на твердость α-твердого раствора в зоне, примыкающей к зоне нитридов на расстоянии ~ 0,025 мм. А на втором этапе находили формулы влияния легирующих элементов на распределение твердости от поверхности вглубь стальной основы с учетом коэффициента термодинамической активности азота.

Твердость азотированного слоя в начале α - твердого раствора представляется как сумма приращения твердости слоя за счет азота и легирующих элементов, и твердости подложки (термически обработанной упрочняемой стали) [5], [11].

13-01-2021 17-43-45     (1)

На основании проведенных экспериментов и анализа литературных данных были разработанные формулы для расчета приращения твердости 13-01-2021 17-43-53 в зависимости от содержания каждого легирующего элемента в материале подложки, которые позволяют предварительно оценить с учетом правила аддитивности возможную суммарную твердость азотированной стали при совокупном влиянии этих элементов. Полученное расчетное значение твердости характеризует твердость в начале α – слоя. Далее представленная модель предусматривает расчет распределения твердости, исходя из рассчитанной или экспериментально определенной толщины α – слоя и распределения азота.

Влияние легирующих элементов в стали на приращение твердости

Исследование влияния содержания легирующих элементов на твердость α – твердого раствора азотированного слоя проводилось на различных конструкционных сталях, в которых изменялась концентрация только одного из элементов. При этом сделано допущение, что содержание легирующих элементов на всем протяжении слоя соответствует их среднему содержанию в стали. Полученные зависимости влияния каждого элемента были аппроксимированы математическими формулами с высокой степенью достоверности (Таблица 1).

Суммарное значение твердости α - слоя при воздействии совокупности некоторого количества легирующих элементов определялось по формуле:

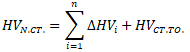13-01-2021 17-44-03    (2)  

Таблица 1 – Влияние содержания легирующих элементов на приращение твердости α - слоя

Легирующий элемент Расчетная формула Достоверность, R2
1 Ni 5,1095x3 - 54,795x2 + 192,96x + 92,079 0,991
2 Si 47,643x + 150 0,9967
3 Mn 72,558x + 153,41 0,9991
4 V 387,68x0,4038 0,9962
5 Cr 8,1988x3 - 94,883x2 + 385,87x + 105,29 0,9968
6 Al 4,193x3 - 65,062x2 + 375,31x + 101,12 0,9975
7 Mo 19,038x3 - 213,94x2 + 715,2x - 2,4302 0,9815
8 W 3,2338x3 - 35,937x2 + 128,76x + 97,625 0,9909
9 Ti 8,2836x3 - 97,2x2 + 399,83x + 101,85 0,9968
Примечание: х – содержание соответствующего легирующего элемента  

Расчет коэффициента термодинамической активности азота

Коэффициент термодинамической активности азота (γN) представляет собой меру отклонения реального раствора от равновесного состояния. Он тесно связан с термодинамической активностью азота и с распределением его по толщине слоя. При этом по мере увеличения расстояния от поверхности наблюдается снижение концентрации азота и, как следствие, повышение коэффициента активности и приближение его к единице. Следовательно, он характеризует способность к поглощению азота конкретной сталью или сплавом и уменьшается от поверхности до сердцевины детали.

13-01-2021 17-55-52      (3)

где СN – максимальное содержание азота в слое; С0 – равновесное содержание азота в α - железе; 13-01-2021 17-46-47 – термодинамический коэффициент активности азота в железе; 13-01-2021 17-46-56 - термодинамический коэффициент активности азота в легированной стали; 13-01-2021 17-51-41 - максимальное содержание азота в легированной стали.

Для расчета распределения твердости по толщине α-слоя наиболее приемлемым подходом является учет термодинамической активности азота в стали в зависимости от содержания легирующих элементов, которое принимается равным среднему содержанию в стали (Таблица 2).

Например, для содержания хрома в интервале до 5% по массе формула имеет вид [3]:

13-01-2021 17-47-05      (4) В этом случае термодинамический коэффициент активности азота от содержания хрома составит: 13-01-2021 17-47-21 при 3% Cr, а концентрация азота в этом случае составит: 13-01-2021 17-47-33     (5)  

Таблица 2 – Влияние легирующих элементов (% по массе) на термодинамический коэффициент активности азота в стали

Легирующий элемент Логарифм активности азота: lgγ(N) Концентрационный интервал, %
1 Cr - 0,54*(% Cr)0,5 0 - 5
- 0,0067(137+%Cr) 5 - 13
2 Si 0,5* (% Si) 0 - 3
3 Mo - 0,29* (% Mo) 0 - 5
4 Mn - 0,21* (% Mn) 0 - 3
- 0,28* (% Mn) 0 - 5
5 V - 0,895* (% V)0,4 0 – 2,5
6 C 0,41* (% C) 0 – 1,0
7 Al 0 Теоретическое влияние
- 0,5*(% Al) Расчетное влияние
8 Ni 0,019* (% Ni) 0 - 5
9 Ti - 0,588* (% Ti) 0 - 2
10 Zr - 0,22* (% Zr) 0 – 0,15
11 Nb - 0,59* (% Mo) 0 – 0,35
12 W - 0,118* (% W) 0 – 8,8
13 S 0,8*(%S) S > 0,1
14 Pb 0,7*(%Pb)0,5 Pb > 0,1
  Термодинамический коэффициент активности азота стали от ряда легирующих элементов определяли по формуле:13-01-2021 17-56-22      (6) В соответствии с полученным значением определяется максимальное содержание азота в α - твердом растворе 13-01-2021 17-56-27     (7)

Концентрация азота по толщине α - слоя в конкретной точке (yi) определяется по формуле, полученной из решения уравнений Фика и кинетическим закономерностям роста фаз слоя:

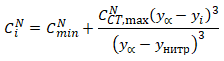13-01-2021 17-56-34       (8)

где: 13-01-2021 17-56-57 – минимальная концентрация азота в стали, не вызывающая изменение структуры и свойств;

 yα – толщина слоя α – твердого раствора, определенная металлографическим методом;

 yнитр – толщина слоя нитридов.

Сравнение рассчитанных значений твердости в начале α – слоя с экспериментальными данными (Таблица 3), полученными при обработке в расплавах солей, показал хорошее соответствие.

Распределение твердости по сечению слоя коррелирует с распределением азота с соответствующим коэффициентом активности в каждой точке слоя (13-01-2021 17-57-07). В результате проведенной статистической обработки результатов экспериментальных данных была разработана полуэмпирическая формула для расчета приращения твердости в точке (i) α-слоя:

13-01-2021 18-00-16        (9) Тогда твердость слоя в точке (i) составит: 13-01-2021 18-00-24       (10)  

Таблица 3 – Сравнительные данные экспериментов и расчета твердости

Марка стали Твердость на расстоянии 25мкм от поверхности, кгс/мм2 Погрешность, %
Эксперимент Расчет
10 280 297 6,07
35 375 350 6,9
80 405 438 8,2
35ХГМ 650 660 1,5
30Х2МНЮА 840 821 2,2
22ГФС 610 605 0,8
40Х5МФС 1190 1169 1,9
Х 700 649 7,2
30Х3М 880 865 2,9
35Х2Н4М 685 678 1,2
35ХГН2 630 621 1,2
А45Г2 450 446 0,9
АС15Г 315 318 0,9
Примечание: условия обработки: 570 оС; 1,5 ч; 38 % CNO-  

Полученные расчетные результаты численного эксперимента (Рис. 1) показывают хорошее совпадение с экспериментальными данными, а представленная эмпирическая методика позволяет легко разработать алгоритм расчета.

 

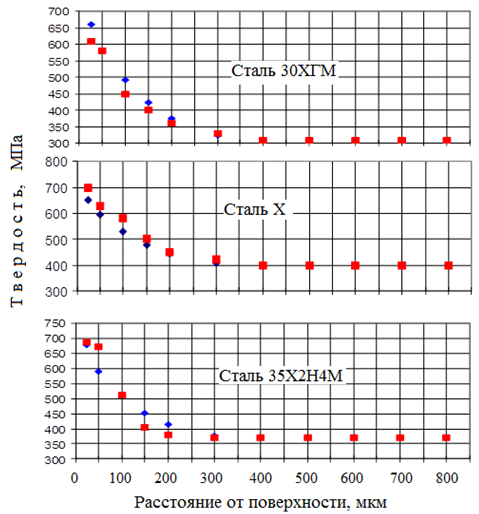
13-01-2021 18-01-20

Рис. 1 – Сравнение результатов реальных и численных экспериментов: 13-01-2021 18-02-04 Рассчитанные значения; 13-01-2021 18-02-11 Экспериментальные значения

Примечание: условия обработки: 570 оС; 1,5 ч; 38 % CNO-

  Заключение

В работе на основании проведенных обширных экспериментов азотирования в газовых, жидких и твердых средах установлено влияние легирующих элементов обрабатываемых конструкционных сталей на кинетику роста фаз слоя и твердость. Разработана и апробирована методика предиктивного расчета распределения содержания азота и твердости по толщине α – твердого раствора азотированного слоя. Методика предусматривает применение термодинамического коэффициента активности азота и его зависимости от суммарного влияния содержания легирующих элементов, что и было установлено в данной работе. Численные эксперименты расчета выходных параметров азотированных слоев на различных сталях показали более высокое совпадение с экспериментальными данными, чем рекомендуемые в литературных источниках методики расчета.

Конфликт интересов Не указан. Conflict of Interest None declared.

Список литературы / References

  1. Арзамасов Б.Н. Ионная химико-термическая обработка сплавов / Б.Н. Арзамасов, А.Г. Братухин, Ю.С. Елисеев, Т.А. Панайоти. – М.: Изд-во МГТУ им Н.Э. Баумана - 1999. – 400 с.
  2. Лахтин Ю.М. Химико-термическая обработка металлов / Ю.М. Лахтин, Б.Н. Арзамасов. – М.: Металлургия, 1985, 256 с.
  3. Ratajski J. Model of growth kinetics of nitride layers in the binary Fe – N system/ J. Ratajski // Nitriding technology. Proceedings the 9th international seminar. Warsaw, Poland 2003. P. 149-159.
  4. Mittemeijer E.J. Thermodynamics, kinetics and process control of nitriding / E.J. Mittemeijer, M.A.J. Somers // Surface Engineering, 1997, Vol. 13, N6, p. 483-497.
  5. Лахтин Ю.М. Теория и технология азотирования / Ю.М. Лахтин, Я.Д. Коган, Х.-Й. Шпис, З. Бемер. - М.: Металлургия, 1991, - 320 с.
  6. Герасимов С.А. Структура и износостойкость азотированных конструкционных сталей и сплавов / С.А. Герасимов, Л.И. Куксенова, В.Г. Лаптева. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2014. – 518 с.
  7. Исламкулов К.М. Моделирование процесса упрочнения малоуглеродистых сталей / К.М. Исламкулов, Ж.Т. Айменов, Д.У. Смагулов // Успехи современного естествознания. – 2014. – № 10. – С. 73-75;
  8. Дин Кай Цзянь. Сопоставление твердорастворного и нитридного упрочнения азотированного хромоникелевого сплава на основе разработанной математической модели / Дин Кай Цзянь, М.Ю. Семенов// ВЕСТНИК ПНИП. - Машиностроение, материаловедение, 2016. Т. 18, № 3. – С. 41 – 51.
  9. Петрова Л.Г. Моделирование процессов внутреннего азотирования жаропрочных сталей и сплавов / Л.Г. Петрова: дис. … д-ра техн. наук. − М., 2001. − 402 с.
  10. Солодкин Г.А. Расчет влияния легирующих элементов на твердость конструкционных сталей при газовом азотировании / Г.А. Солодкин, A.A. Булгач, Л.А. Глиберман // Применение ЭВМ в металловедении и металлообработке: Сб. научн. Тр./ МАДИ. – М.: МАДИ. 1986. – С. 32-42.
  11. Krukovich M.G. Simulation of the Nitride Process / M.G. Krukovich // Metal Science and Heat Treatment. V.46; Issue 1, 2; P. 25 – 31; 2004.

Список литературы на английском языке / References in English

  1. Arzamasov B. N. Ionnaia khimiko-termicheskaia obrabotka splavov [Ionic Chemical and Heat Treatment of Alloys] / B. N. arzamasov, A. G. Bratukhin, Yu. S. Eliseev et al. - M.: Publishing House of the Bauman Moscow State Technical University. -1999. - 400 p. [in Russian]
  2. Lakhtin Yu. M. Khimiko-termicheskaia obrabotka metallov [Chemical and Heat Treatment of Metals] / Yu. M. Lakhtin, B. N. Arzamasov. - M.: metallurgy, 1985, 256 p. [in Russian]
  3. Ratajski J. Model of growth kinetics of nitride layers in the binary Fe – N system / J. Ratajski // Nitriding technology. Proceedings the 9th international seminar. Warsaw, Poland 2003. P. 149-159.
  4. Mittemeijer E.J. Thermodynamics, kinetics and process control of nitriding / E.J. Mittemeijer, M.A.J. Somers // Surface Engineering, 1997, Vol. 13, N 6, p. 483-497.
  5. Lakhtin Yu. M. Teoriia i tekhnologiia azotirovaniia [Theory and Technology of Nitriding] / Yu. M. Lakhtin, Ya. D. Kogan, Kh. Y. Shpis et al., Moscow: Metallugriya, 1991, 320 p. [in Russian]
  6. Gerasimov S. A. Struktura i iznosostoikost' azotirovannykh konstruktsionnykh stalei i splavov [Structure and Wear Resistance of Nitrided Engineering Steel and Alloys] / Gerasimov, L. I. Kuksenova, V. G. Lapteva - M.: Publishing House of the Bauman Moscow State Technical University. , 2014. - 518 p. [in Russian]
  7. Islamkulov K. M. Modelirovanie protsessa uprochneniia malouglerodistykh stalei [Simulation of the Hardening Process in Low-Carbon Steel] / K. M. Islamkulov, Zh. T. Aimenov, D. U. Smagulov // Uspekhi sovremennogo estestvoznaniia [Advances in Modern Natural Science]. - 2014. - No. 10. - pp. 73-75 [in Russian]
  8. Ding Kai Tsien. Sopostavlenie tverdorastvornogo i nitridnogo uprochneniia azotirovannogo khromonikelevogo splava na osnove razrabotannoi matematicheskoi modeli [Comparison of Solid Solution and Nitride Hardening of Nitrided Chromium-Nickel Alloy Based on the Developed Mathematical Model] / Ding Kai Tsien, M. Yu. Semenov // [Bulletin of the Perm National Research Polytechnic University]. - Mechanical engineering, materials science, 2016. Vol. 18, No. 3. - pp. 41-51 [in Russian]
  9. Petrova L. G. Modelirovanie protsessov vnutrennego azotirovaniia zharoprochnykh stalei i splavov [Modeling of Internal Nitriding Processes for Heat-Resistant Steel and Alloys]: Candidate’s thesis. - Moscow, 2001. - 402 p. [in Russian]
  10. Solodkin G. A. Raschet vliianiia legiruiushchikh elementov na tverdost' konstruktsionnykh stalei pri gazovom azotirovanii [Calculation of the Effect of Alloying Elements on the Hardness of Structural Steels During Gas Nitriding]/ G. A. Solodkin, A. A. Bulgach, L. A. Gleberman // Primenenie EVM v metallovedenii i metalloobrabotke: Sb. nauchn. Tr. [The use of computers in physical metallurgy and metal working: A Collection of Studies] / MADI. - M.: MADI. 1986. - pp. 32-42 [in Russian]
  11. Krukovich M.G. Simulation of the Nitride Process / M.G. Krukovich. Metal Science and Heat Treatment. V.46; Issue 1, 2; P. 25 – 31; 2004.