PARALLEL TRANSMISSION OF BINARY MESSAGES BY OVERLAPPING SIGNALS
ПАРАЛЛЕЛЬНАЯ ПЕРЕДАЧА ДВОИЧНЫХ СООБЩЕНИЙ ПЕРЕКРЫВАЮЩИМИСЯ СИГНАЛАМИ
Научная статья
Вершинин В.А. *
ORCID: 0000-0002-0803-0680,
Рыбинский государственный авиационный технический университет, Рыбинск, Россия
* Корреспондирующий автор (vershinin-vladimir[at]yandex.ru)
АннотацияВ статье рассматривается параллельная передача двоичных сообщений. Перед передачей двоичное сообщение делится на блоки. Элементы блоков поступают для передачи одновременно и передаются с использованием предлагаемых ортогональных сигналов одинаковой длительности. Сигналы последовательно передаваемых блоков частично перекрываются во времени. Проанализированы удельные затраты полосы частот, пик-фактор и помехоустойчивость передачи. Использование предлагаемых сигналов по сравнению с синусоидальными ортогональными сигналами позволяет увеличить скорость спада боковых лепестков спектральной плотности мощности и уменьшить внеполосные излучения. При этом практически не ухудшается помехоустойчивость передачи.
Ключевые слова: параллельная передача, перекрывающиеся сигналы, ортогональные сигналы, полоса частот, внеполосные излучения, помехоустойчивость, пик-фактор.
PARALLEL TRANSMISSION OF BINARY MESSAGES BY OVERLAPPING SIGNALS
Research article
Vershinin V.A. *
ORCID: 0000-0002-0803-0680,
Rybinsk State Aviation Technical University, Rybinsk, Russia
* Corresponding author (vershinin-vladimir[at]yandex.ru)
AbstractThis paper discusses the parallel transmission of binary messages. Before starting the transmission process, a binary message is divided into blocks. The block elements come for transmission at the same time and are transmitted with the use of the proposed orthogonal signals of the same duration. The signals of sequentially transmitted blocks partially overlap in time. The specific costs of the frequency band, the peak factor, and the noise immunity of the transmission are analyzed. The use of the proposed signals in comparison with sinusoidal orthogonal signals can increase the decay rate of the side lobes of the power spectral density and reduce out-of-band emissions. In this case, the noise immunity of the transmission practically does not deteriorate.
Keywords: parallel transmission, overlapping signals, orthogonal signals, frequency band, out-of-band emissions, noise immunity, peak factor.
ВведениеВ классическом варианте метод параллельной передачи заключается в одновременной передаче блоков из L элементов сообщения с использованием L сигналов длительностью T ортогональных на этом интервале. Блоки поступают для передачи с интервалом T. Таким образом, сигналы, соответствующие элементам каждого блока, полностью перекрываются во времени, а сигналы, соответствующие последовательно передаваемым блокам не перекрываются во времени. Прием ведется на основе ортогонального разделения сигналов. Необходимо отметить, что основы теории линейного (в том числе ортогонального) уплотнения и разделения сигналов разработаны советским ученым Д.В.Агеевым в 1935 году [1]. Заметим также, что в основе широко используемой технологии OFDM (orthogonal frequency division multiplexing) лежит параллельная передача сообщений с использованием ортогональных синусоидальных сигналов. Одним из недостатков OFDM является малая скорость спада боковых лепестков спектральной плотности мощности, что приводит к увеличению внеполосных излучений. Стремление избавиться от этого недостатка приводит обычно к увеличению удельных затрат полосы или снижению помехоустойчивости.
В статье рассматривается параллельная передача двоичных сообщений, когда блоки поступают для передачи с интервалом и передаются с использованием L элементарных сигналов длительностью T ортогональных на этом интервале. В этом случае сигнал, соответствующий передаваемому блоку частично перекрывается с сигналом предыдущего блока и сигналом последующего блока. При приеме это приводит к возникновению перекрестных помех. Целью данной работы является исследование эффективности использования для такой параллельной передачи ортогональных сигналов вида:
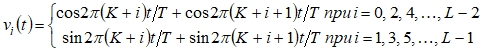
Эти сигналы определены на интервале времени ![]() , вне указанного интервала сигналы равны нулю. K – целое положительное число, определяющее расположение полосы частот, занимаемой сигналом на выходе модулятора. Значение L предполагается четным.
, вне указанного интервала сигналы равны нулю. K – целое положительное число, определяющее расположение полосы частот, занимаемой сигналом на выходе модулятора. Значение L предполагается четным.
При ![]() :
:
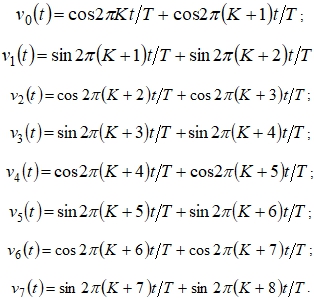
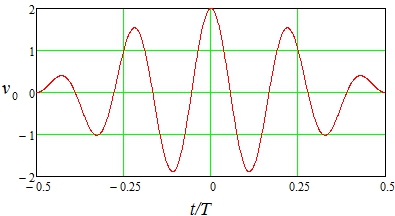
Рис. 1 – Нормированный сигнал![]()
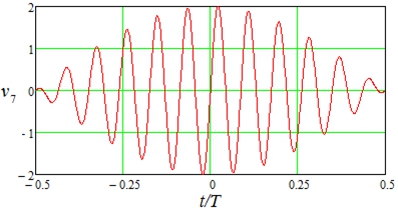
Рис. 2 – Нормированный сигнал![]()
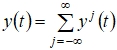 (3)
где
(3)
где Необходимо отметить, что применение сигналов вида (1) в различных вариантах для передачи двоичных сообщений рассматривалось в [2 – 7]. Причем в [2] рассматривалась параллельная передача, а в [6] и [7] – с использованием перекрывающихся во времени сигналов.
Полоса частот
Определим полосу частот, занимаемую сигналом в виде (2). Этот сигнал в общем случае является случайным сигналом. Будем считать элементы двоичного сообщения независимыми случайными величинами, принимающими два значения с равной вероятностью. Полоса частот F, занимаемая сигналом определяется, исходя из спектральной плотности мощности этого сигнала ![]() , где f – частота.
, где f – частота.
Спектральная плотность мощности сигнала (2)
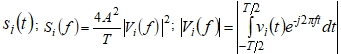 . Тогда можно получить:
. Тогда можно получить:
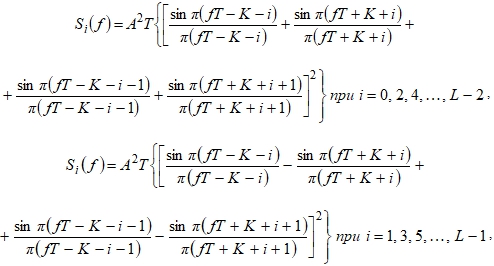
Средняя мощность сигнала (2) ![]() ; средняя энергия сигнала
; средняя энергия сигнала ![]() на интервале
на интервале ![]() ; средняя энергия сигнала, приходящаяся на элемент передаваемого сообщения
; средняя энергия сигнала, приходящаяся на элемент передаваемого сообщения ![]()
С использованием (4) получена зависимость при ![]() , приведенная на рис. 3 в виде
, приведенная на рис. 3 в виде ![]() , где
, где ![]() – максимальное значение
– максимальное значение ![]() .
.
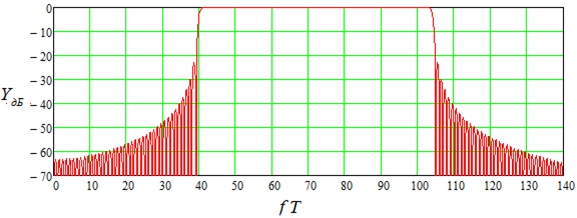
Рис. 3 – Зависимость ![]()
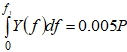 ;
;
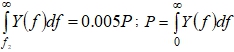
Полосу частот F, занимаемую сигналом (2), используя (4) и (5) вычислим при ![]() . Эта полоса равна
. Эта полоса равна ![]() соответственно. Удельные затраты полосы, определяемые как
соответственно. Удельные затраты полосы, определяемые как ![]() – скорость передачи информации (бит/с), равны 0.496 и 0.495.
– скорость передачи информации (бит/с), равны 0.496 и 0.495.
Вторым способом полоса частот определяется непосредственно с использованием зависимости ![]() по уровню –30 дБ. При
по уровню –30 дБ. При ![]() она равна
она равна ![]() , а удельные затраты полосы 0.531 и 0.516.
, а удельные затраты полосы 0.531 и 0.516.
Определим пик-фактор сигнала (2) как отношение максимального значения сигнала к ![]() . Тогда значению
. Тогда значению ![]() соответствует пик-фактор 7.92 и 11.0.
соответствует пик-фактор 7.92 и 11.0.
Помехоустойчивость
Оценим помехоустойчивость параллельной передачи при использовании ортогональных сигналов (1). Будем полагать, что на сигнал вида (3), в линии связи воздействует аддитивная помеха ![]() в виде белого шума с односторонней спектральной плотностью мощности N. Тогда на входе демодулятора имеет место сигнал
в виде белого шума с односторонней спектральной плотностью мощности N. Тогда на входе демодулятора имеет место сигнал
![]() (6)
(6)
Демодулятор принимает решение о принятом значении m-го элемента j -го блока (![]() ) на основе корреляционной обработки сигнала (6) на интервале
) на основе корреляционной обработки сигнала (6) на интервале ![]() передачи j-го блока [10]:
передачи j-го блока [10]:
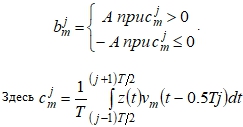 .
.
Рассмотрим структуру ![]() . С учетом (3) и (6):
. С учетом (3) и (6):
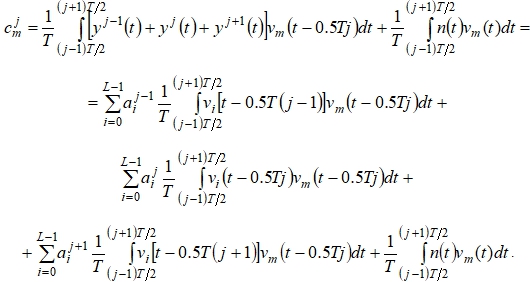
Здесь 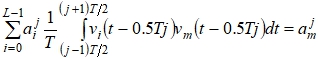 из-за ортогональности сигналов (1);
из-за ортогональности сигналов (1); ![]() – переданный элемент блока
– переданный элемент блока ![]() , из-за наличия помех принятый элемент
, из-за наличия помех принятый элемент ![]() может отличаться от
может отличаться от ![]() .
. 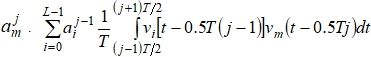 – перекрестная помеха, связанная с влиянием передачи элементов
– перекрестная помеха, связанная с влиянием передачи элементов ![]() предыдущего блока.
предыдущего блока. 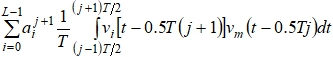 – перекрестная помеха, связанная с влиянием передачи элементов
– перекрестная помеха, связанная с влиянием передачи элементов ![]()
![]() следующего блока.
следующего блока. 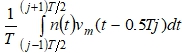 – слагаемое, связанное с влиянием помехи n(t), является случайной величиной, распределенной по нормальному закону [10] с нулевым математическим ожиданием и дисперсией
– слагаемое, связанное с влиянием помехи n(t), является случайной величиной, распределенной по нормальному закону [10] с нулевым математическим ожиданием и дисперсией ![]() .
.
Аналитически оценить помехоустойчивость с учетом перекрестных помех сложно и практически ненаглядно, поэтому дальнейший анализ будем проводить с использованием моделирования в среде Matlab. Для этого сигналы при передаче j-го блока на интервале ![]() рассматриваются в дискретные моменты времени
рассматриваются в дискретные моменты времени ![]() . Здесь
. Здесь ![]() – период дискретизации;
– период дискретизации; ![]() – число дискретных моментов времени на интервале
– число дискретных моментов времени на интервале ![]() , это число должно быть четным. При этом будем иметь в виду, что при достаточно малых
, это число должно быть четным. При этом будем иметь в виду, что при достаточно малых ![]() :
:
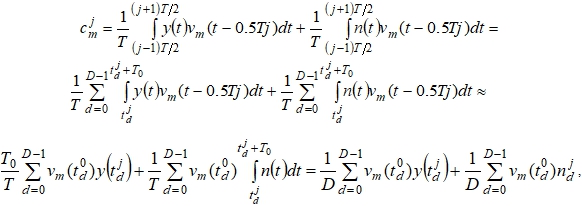
где 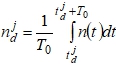 – значения помехи в дискретные моменты времени на интервале передачи j-го блока. Эти значения имеют [10] нормальное распределение с нулевым математическим ожиданием и дисперсией
– значения помехи в дискретные моменты времени на интервале передачи j-го блока. Эти значения имеют [10] нормальное распределение с нулевым математическим ожиданием и дисперсией ![]() . Воздействие помехи на сигнал принято характеризовать величиной
. Воздействие помехи на сигнал принято характеризовать величиной ![]() , где
, где ![]() – средняя энергия сигнала
– средняя энергия сигнала ![]() на интервале
на интервале ![]() , приходящаяся на элемент передаваемого сообщения,
, приходящаяся на элемент передаваемого сообщения, ![]() .
.
Тогда
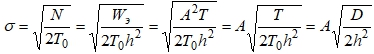
матрицу v с элементами ![]()
![]() ;
;
матрицу ![]() , у которой столбцы
, у которой столбцы ![]()
![]() соответственно равны столбцам матрицы v, а элементы столбцов
соответственно равны столбцам матрицы v, а элементы столбцов ![]() матрицы
матрицы ![]() равны нулю;
равны нулю;
матрицу ![]() , у которой столбцы
, у которой столбцы ![]() соответственно равны столбцам
соответственно равны столбцам ![]() матрицы v, а элементы столбцов матрицы равны нулю;
матрицы v, а элементы столбцов матрицы равны нулю;
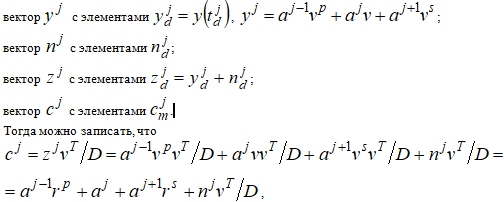
где ![]() – транспонированная матрица относительно матрицы
– транспонированная матрица относительно матрицы ![]() – матрица, определяющая перекрестную помеху, связанную с влиянием передачи элементов предыдущего блока;
– матрица, определяющая перекрестную помеху, связанную с влиянием передачи элементов предыдущего блока; ![]() – матрица, определяющая перекрестная помеху, связанную с влиянием передачи элементов следующего блока. Половина элементов столбцов матриц
– матрица, определяющая перекрестная помеху, связанную с влиянием передачи элементов следующего блока. Половина элементов столбцов матриц ![]() равна нулю. Отличные от нуля элементы создают перекрестную помеху. Нетрудно также получить, что
равна нулю. Отличные от нуля элементы создают перекрестную помеху. Нетрудно также получить, что ![]() .
.
- function er=gr2(h2,U,L)
- rng('default');
- K=4;
- D=260;
- A=1;
- T=1;
- T0=T/D;
- v=zeros(L,D);
- vp=zeros(L,D);
- vs=zeros(L,D);
- td=-T/2:T0:T/2-Td;
- for i=0:2:L-2
- v(i+1,:)=cos(2*pi*(K+i)*td/T)+cos(2*pi*(K+i+1)*td/T);
- end
- for i=1:2:L-1
- v(i+1,:)=sin(2*pi*(K+i)*td/T)+sin(2*pi*(K+i+1)*td/T);
- end
- vp(:,1:D/2)=v(:,D/2+1:D);
- vs(:,D/2+1:D)=v(:,1:D/2);
- er=0;
- sigma=A*sqrt(D/(2*h2));
- ap=2*A*round(rand(1,L))-1;
- a=2*A*round(rand(1,L))-1;
- as=2*A*round(rand(1,L))-1;
- n=normrnd(0,sigma,1,D);
- for j=1:U
- y=ap*vp+a*v+as*vs;
- z=y+n;
- c=z*v'/D;
- b=2*(c >=0)-1;
- er=er+ sum(ne(b,a));
- ap=a;
- a=as;
- as=2*A*round(rand(1,L))-1;
- n(1:D/2)=n(D/2+1:D);
- n(D/2+1:D)= normrnd(0,sigma,1,D/2);
- end
- end
- Определяется функция вычисляющая число ошибочно принятых элементов при заданных значениях h2 , U и L.
- Начинается подготовительная часть программы. Устанавливаются настройки генератора случайных чисел в значения по умолчанию.
- Устанавливается значение K.
- Устанавливается значение D.
- Устанавливается значение A.
- Устанавливается значение T.
- Определяется период дискретизации T0.
- Определяется матрица v с нулевыми элементами.
- Определяется матрица
 с нулевыми элементами.
с нулевыми элементами. - Определяется матрица
 с нулевыми элементами.
с нулевыми элементами. - Определяется вектор, элементы которого соответствуют дискретным моментам времени
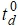 .
. - Задается параметр циклов формирования четных строк матрицы v.
- Определяются четные строки матрицы v.
- Конец циклов формирования четных строк матрицы v.
- Задается параметр циклов формирования нечетных строк матрицы v.
- Определяются нечетные строки матрицы v.
- Конец циклов формирования нечетных строк матрицы v.
- Определяются строки матрицы
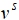 .
. - Определяются строки матрицы
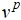 .
. - Устанавливается нулевое значение переменной результата
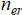 .
. - Определяется
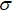 .
. - Определяется начальное значение вектора, соответствующего
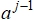 .
. - Определяется начальное значение вектора, соответствующего
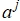 .
. - Определяется начальное значение вектора, соответствующего
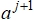 .
. - Формируется начальное значение вектора дискретных значений помехи
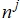 .
. - Задается параметр циклов, моделирующих передачу U блоков.
- Формируется вектор дискретных значений передаваемого сигнала
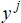 .
. - Формируется вектор дискретных значений принимаемого сигнала
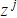 .
. - Определяется вектор
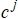 .
. - Определяется вектор принятых значений передаваемых элементов
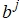 .
. - Вычисляется сумма количества ошибок в текущем и предыдущих испытаниях.
- Определяется новое значение вектора, соответствующего
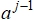 .
. - Определяется новое значение вектора, соответствующего
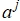 .
. - Определяется новое значение вектора, соответствующего
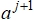 .
. - Формируется новое значение первой половины значений элементов вектора
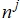 .
. - Формируется новое значение второй половины значений элементов вектора
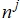 .
. - Конец циклов, моделирующих передачу U блоков.
- Конец программы моделирования.
Результаты моделирования с помощью приведенной выше программы приведены в таблице 1. Моделирование производилось при ![]() и различных значениях
и различных значениях ![]() . В результате были получены значения числа ошибок
. В результате были получены значения числа ошибок ![]() при передаче
при передаче ![]() элементов двоичного сообщения. Затем с помощью функции berconfint пакета Matlab определена оценка вероятности ошибки
элементов двоичного сообщения. Затем с помощью функции berconfint пакета Matlab определена оценка вероятности ошибки ![]() , нижняя
, нижняя ![]() и верхняя
и верхняя ![]() граница оценки с доверительной вероятностью 0.95.
граница оценки с доверительной вероятностью 0.95.
Таблица 1 – Результаты моделирования
Рассмотрим лежащую в основе технологии OFDM параллельную передачу двоичных сообщений с помощью ортогональных синусоидальных сигналов. Определим на интервале времени ![]() множество ортогональных синусоидальных сигналов следующего вида:
множество ортогональных синусоидальных сигналов следующего вида:
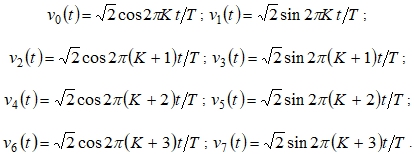
Сигнал на выходе модулятора с использованием сигналов (7)
![]() (8)
(8)
где ![]() . Энергия сигнала, приходящаяся на элемент передаваемого сообщения
. Энергия сигнала, приходящаяся на элемент передаваемого сообщения ![]() . Заметим, что в этом случае (в отличие от (2)) сигнал, соответствующий передаваемому блоку не перекрывается с сигналами других блоков.
. Заметим, что в этом случае (в отличие от (2)) сигнал, соответствующий передаваемому блоку не перекрывается с сигналами других блоков.
Спектральная плотность мощности сигнала (8)
![]()
где
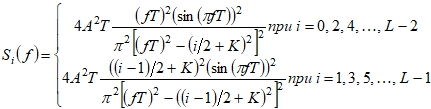
Можно получить:
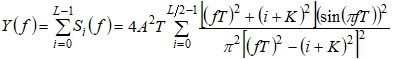 (9)
(9)
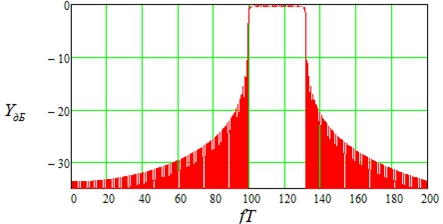
Рис. 5 – Зависимость ![]()
На основании (9) полосу частот F вычислим (первый способ) с использованием (5) при ![]() для значений
для значений ![]() . Эта полоса равна соответственно
. Эта полоса равна соответственно ![]() . Удельные затраты полосы равны 0.538 и 0.500. При определении полосы частот вторым способом по уровню –30 дБ она равна
. Удельные затраты полосы равны 0.538 и 0.500. При определении полосы частот вторым способом по уровню –30 дБ она равна ![]() , а удельные затраты полосы 1.72 и 1.41. Значениям
, а удельные затраты полосы 1.72 и 1.41. Значениям ![]() соответствует пик-фактор 7.90 и 11.0.
соответствует пик-фактор 7.90 и 11.0.
Существенное увеличение удельных затрат при определении полосы вторым способом связано с малой скоростью спада боковых лепестков спектральной плотности мощности при использовании сигналов (8). В то же время, при использовании частично перекрывающихся сигналов (2) удельные затраты при определении полосы вторым способом возрастают незначительно.
Вероятность ошибки при корреляционном приеме сигнала (8) может быть определена формулой [10]:
![]()
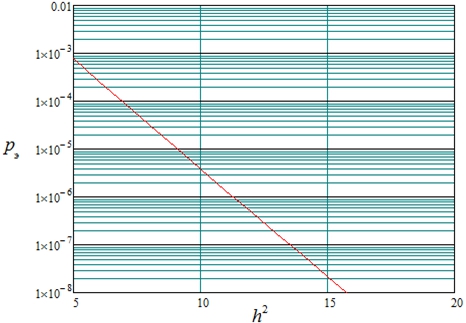
Рис. 6 – Зависимости вероятности ошибки от ![]()
Сопоставляя данные таблицы 1 с рис. 6 можно заключить, что использование частично перекрывающихся сигналов (2) на основе сигналов (1) практически не ухудшает помехоустойчивость передачи по сравнению с использованием сигналов (8) на основе сигналов (7).
Заключение
Использование при параллельной передаче частично перекрывающихся сигналов на основе предлагаемых ортогональных сигналов по сравнению с неперекрывающимися синусоидальными ортогональными сигналами позволяет получить лучшие удельные затраты полосы, увеличить скорость спада боковых лепестков спектральной плотности мощности (уменьшить внеполосные излучения). При этом помехоустойчивость практически не ухудшается.
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Агеев. Д.В. Основы теории линейной селекции / Агеев. Д.В. // Научно-техн. сб. Ленингр. электротехн. ин-та связи.– 1935.– N
- Вершинин В.А. Параллельная передача двоичных сообщений линейно независимыми сигналами / Вершинин В.А. // Международный научно-исследовательский журнал. 2019. N6(84).
- Передача дискретных сообщений/ Вершинин В.А. Рыбинская государственная авиационная технологическая академия им. П.А. Соловьева. Рыбинск, 2002.– 82 с.– Деп. в ВИНИТИ 17.12. 2002, № 2196-В2002
- Вершинин В.А. Передача двоичных сообщений симплексными сигналами [Электронный ресурс] / В.А. Вершинин // Журнал радиоэлектроники: электронный журнал. 2013. N URL: http://jre.cplire.ru/jre/nov13/5/text.pdf (дата обращения: 12.09.2019)
- Vershinin V.A. The transmission of binary messages special biorthogonal signals [Electronic resource] / Vershinin V.A. // Eastern European Scientific Journal.– 2015.– N4.– URL: http://www.auris-archiv.de/mediapool/99/990918/data/DOI_10.12851_EESJ201508.pdf (accessed: 12.09.2019)
- Вершинин В.А. Передача двоичных сообщений перекрывающимися сигналами [Электронный источник] / Вершинин В.А. // Журнал радиоэлектроники: электронный журнал. 2017. N - URL: http://jre.cplire.ru/jre/oct17/5/text.pdf (дата обращения: 12.09.2019)
- Вершинин В.А. Поэлементный прием и прием в целом при перекрывающихся элементарных сигналах [Электронный ресурс] / Вершинин В.А. // Журнал радиоэлектроники: электронный журнал. 2018. N URL: http://jre.cplire.ru/jre/oct18/5/text.pdf (дата обращения: 12.09.2019)
- Сергиенко А.Б. Цифровая связь: Учеб. пособие / Сергиенко А.Б. СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2012.– 164 с.
- Скляр Бернард. Цифровая связь. Теоретические основы и практическое применение / Скляр Бернард. 2-е изд.: Пер. с англ.– М.: Издательский дом «Вильямс», 2003.– 1104 с.
- Теория электрической связи: Учебник для вузов / А.Г. Зюко, Д.Д. Кловский, В.И. Коржик, М.В. Назаров; под ред. Д.Д. Кловского. – М. : Радио и связь, 1998.– 432 с.
Список литературы на английском языке / References in English
- D.V. Osnovy teorii lineynoy selektsii [Fundamentals of the theory of linear selection] . Ageyev. D.V. // Nauchno-tekhn. sb. Leningr. elektrotekhn. in-ta svyazi [Scientific and technical collection of Leningrad electrotechnical Institute of communications].– 1935.– N10. [in Russian]
- Vershinin V.A. Parallel'naya peredacha dvoichnyh soobshchenij linejno nezavisimymi signalami [Parallel transmission of binary messages by linearly independent signals] / Vershinin V.A. // Mezhdunarodnyj nauchno-issledovatel'skij zhurnal [International research journal]. N6(84). [in Russian]
- Peredacha diskretnyh soobshchenij [Transmission of discrete messages] / Vershinin V.A. Rybinskaya gosu-darstvennaya aviacionnaya tekhnologicheskaya akademiya im. P.A. Solov'eva. Rybinsk, 2002.– 82 p.– Dep. v VINITI 17.12. 2002, № 2196-V2002. [in Russian]
- Vershinin V.A. Peredacha dvoichnyh soobshchenij simpleksnymi signalami [Transmission of binary messages by simplex signals] [Electronic resource] / Vershinin V.A. // ZHurnal radioelektroniki: elektronnyj zhurnal [Journal of radio electronics: electronic journal]. 2013. N11. URL: http://jre.cplire.ru/jre/nov13/5/text.pdf (accessed: 12.09.2019) [in Russian]
- Vershinin V.A. The transmission of binary messages special special biorthogonal signals [Electronic resource] / Vershinin V.A. // Eastern European Scientific Journal.– 2015.– N4.– URL: http://www.auris-archiv.de/mediapool/99/990918/data/DOI_10.12851_EESJ201508.pdf (accessed: 12.09.2019)
- Vershinin V.A. Peredacha dvoichnyh soobshchenij perekryvayushchimisya signalami [Transmission of binary messages by overlapping signals] / Vershinin V.A.// ZHurnal radioelektroniki: elektronnyj zhurnal [Journal of radio electronics: electronic journal]. 2017. N10. URL: http://jre.cplire.ru/jre/oct17/5/text.pdf (accessed: 12.09.2019) [in Russian]
- Vershinin V.A. Vershinin. Poelementnyj priem i priem v celom pri perekry-vayushchihsya elementarnyh signalah [Element-by-element reception and reception in General, when the overlapping of the elementary signals] [Electronic resource] / Vershinin V.A. // ZHurnal radioelektroniki: elektronnyj zhurnal [Journal of radio electronics: electronic journal]. 2018. N10. URL: http://jre.cplire.ru/jre/oct18/5/text.pdf (accessed: 12.09.2019) [in Russian]
- Sergiyenko A.B. Tsifrovaya svyaz: Ucheb. Posobiye [Digital communication: a tutorial] / Sergiyenko A.B. SPb.: Izd-vo SPbGETU «LETI». 2012.– 164 p. [in Russian]
- Sklyar Bernard. Tsifrovaya svyaz. Teoreticheskiye osnovy i prakticheskoye primeneniye / Sklyar Bernard. 2nd edition: Per. s angl.– M.: Izdatelskiy dom «Viliams». 2003.– 1104 p. [in Russian]
- Teoriya elektricheskoy svyazi: Uchebnik dlya vuzov [Theory of telecommunications: the Textbook for high schools] / A.G. Zyuko, D.D. Klovskiy, V.I. Korzhik, M.V. Nazarov; edited by D.D. Klovskogo. – M. : Radio i svyaz. 1998.– 432 p. [in Russian]
