LIFE PREDICTION OF STRUCTURAL DESIGN BASED ON MODELS OF MATERIAL AS A PHYSICAL MEDIUM

Петров М.Г.

Кандидат технических наук, Сибирский научно-исследовательский институт авиации имени С.А. Чаплыгина

ПРОГНОЗИРОВАНИЕ ДОЛГОВЕЧНОСТИ ЭЛЕМЕНТОВ КОНСТРУКЦИЙ НА ОСНОВЕ МОДЕЛЕЙ МАТЕРИАЛА КАК ФИЗИЧЕСКОЙ СРЕДЫ

Аннотация

Методология прогнозирования долговечности конструктивных элементов основывается на кинетической концепции разрушения. Случайные процессы нагружения и температурных флуктуаций моделируются суммированием элементарных случайных функций. Дан ряд примеров расчётных оценок долговечности конструктивных образцов из металлических сплавов при случайных процессах нагружения и когерентных процессах нагружения и нагрева. Эта методология даёт возможность решить те задачи, которые ещё не были решены.

Ключевые слова: долговечность, разрушение, неупругость, случайные воздействия.

Petrov M.G.

PhD in Engineering, Siberian aeronautical research institute named after S.A. Chaplygin

LIFE PREDICTION OF STRUCTURAL DESIGN BASED ON MODELS OF MATERIAL AS A PHYSICAL MEDIUM

Abstract

The methodology of life prediction of structural components is based on the kinetic concept of fracture. Random processes of loading and temperature fluctuations are simulated by a summing of unit random functions. A set of examples is given to calculate life evaluations of structural components under random processes of loading and coherent processes of loading and heating. This methodology enables one to solve those problems which are yet not been worked.

Keywords: longevity, failure, inelasticity, random effects.

Introduction

Danger regions of structures, where macro cracks appear, are subjected to combined effects of various forces. The nominal stresses from several components of loads, which can be inter-correlated random processes, are considered as conditions of failure. The temperature stresses can be another parameter that is related with temperature at critical location of structure partially or completely. The problem on life prediction of structures consists in the determinations of point and time of macro cracks appearance in its elements under concurrent effects of random and determinate constituents of loads and temperature variations.

Solution of the problem

Strength is the interdisciplinary area. The problem is solved in the framework of kinetic concept of fracture, which considers the plastic deformation and accumulation of damages in materials as thermally activated processes [1]. The methodology of life prediction of structure elements supposes the use of three groups of models: models of materials, models of structure elements and models of external effects.

We have introduced new bodies into rheology that describe plastic flow and plastic hysteresis of solids in terms of the theory of rate processes [2, 3]. Composed of rheological bodies, the structural model of material represents formally internal thermodynamic processes in alloys and responds to external effects similar to the material itself. We take, as criterion of fracture, concentration criterion [4, 5], which is accepted obeying for individual structural element of material model.

The models of structure elements are used for reproducing of stress-deformed conditions in danger regions of structure. Their challenge is to associate the nominal stresses (or strains) with the strains in the critical locations of structure elements in time. The model of structure element integrally with the material model forms calculated model of danger region of structure and describes processes of stress and plastic strain variations and of accumulation of damages in critical location.

To simulate the external effects as random processes the theory of random functions has been taken, whereby the random process is presented as a sum of unit random functions (URF) [6, 7]. The equivalent pseudo-random process with discrete spectrum as a sum of harmonic URF is of use as simplest model of actual random process with predetermined standard statistical characteristics. The representing of random process by the sum of URF allows the use of discrete process in the form of piece-linear dependence both in experiments and in computations. The amplitude and frequency modulations of harmonic URF do better about saving in the calculation time and about desired impact.

The temperature and time appear in the solutions of differential equations of material model in explicit form; this being so, the problem of reproducing the arbitrary conditions of structure loading is attacked by piece-linear approximating of actual determined or equivalent pseudo-random processes of force and temperature effects. All processes of external effects break down into time stages, for every of which mathematical expectation, spectral density, and distribution law of current values of process are determined.

The discretion degree of spectrum of equivalent pseudo-random process is adopted as dictated by material of structure element, by stress concentration factor and a root-mean square deviation (RMSD) of process. It can be expressed quantitatively by the following formula:

\[{{D}_{d}}=\sum\limits_{i=1}^{Z}{D_{i}^{2}}/{{D}^{2}}\]

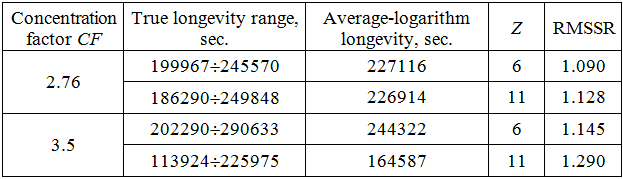
where D_i is dispersion of i-part of process at this located frequency, D is a total dispersion of process, and Z is a number of spectrums lines. If the process is presented by harmonic functions of equal amplitudes, so will D_d = 1/Z [7]. In Table 1 are given the test results of two types structural specimens with variable concentration factor at constant value of spectral density of process presented by distinct number of harmonics of equal amplitudes. Here RMSSR is root-mean square scatter ratio – the life logarithm RMSD’s antilogarithm. It is more descriptive characteristic of scatter.

Table 1 − Test results of structural specimens 8-mm thick and 110-mm wide a duralumin exchanger with two species of notches. Tests performed under pseudo-random loading process presented by a sum of variable number Z of the same amplitude harmonics (RMSD = 35 MPa at zero-mean stress, frequency range 0.5–5.5 Hz; at five specimens for every loading mode)

The fatigue tests of material specimens and sheet with central hole of aluminum alloy 1201 T1 were conducted under poly harmonic pseudo-random process of loading [7]. The life evaluations were performed on four-element material model involving rheological bodies of hysteresis type. The structural model of material itself fulfils the “schematization” of random process like the material, because the damage from subsequent reversal of the load is determined by residual strains in model bodies from earlier reversal.As seen from the table 1, the increase of stress concentration factor requires a decrease of discretion degree of spectrum. On the other hand, the increase of a RMSD of process at constant concentration factor implies increase of process dispersion at critical location, what calls for the same thing.

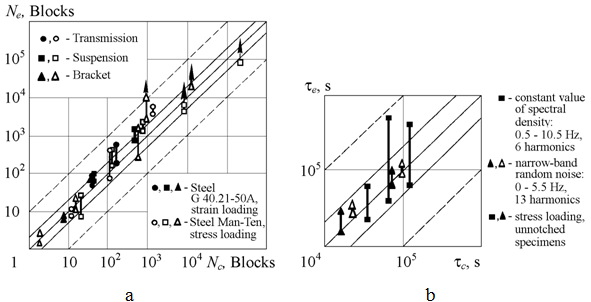
The life calculations of unnotched specimens of steel G 40.21-50A at strain loading [8, 9] and of SAE-type specimens of steel Man-Ten were performed on the SAE cumulative fatigue damage test program [10]. In Fig. 1 (a) is shown the comparison between the calculation results and experiment. The calculated data are given for the case of constant frequency 15 Hz. The greatest deflections in computations are smaller here than with other calculation methods [11]. Fig. 1 (b) is shown the same for aluminum alloy specimens under poly-harmonic loading.

                           

Fig. 1 − Comparison of calculated and experimental life data of specimen: a – loading on the SAE cumulative fatigue damage test program; b – loading under poly-harmonic process [7]

To synthesize inter-correlated processes with equivalent discrete spectra the frequency range of processes is broken down into frequency intervals. For each frequency interval, the required coherent function is determined by separation of process dispersions into coherent and independent parts. That is most merely handled by three techniques: by additive synthesis and through the amplitude or frequency modulation.

In the first case, the dispersion is distributed among harmonics of equal and incommensurable frequencies according to the inter-statistical characteristics of processes. The incommensurable frequencies result from frequency ratios as irrational numbers. In [7] is diagrammed the simultaneous distribution density of current values of processes X and Y for coherent function of 0.5 on a frequency interval Δf by this technique.

In the second case the coherent function is given by the modulation degree that is by fraction of constant amplitudes A_c in amplitude-modulated harmonics of equal frequencies. The combined amplitude of such URF

\[A(t)={{A}_{c}}+{{A}_{v}}{{F}_{m}}(t)\]

where F_m is modulating function. The modulation degree is variable from zero to one and defined by the following expression:

\[{{D}_{m}}={{A}_{v}}/({{A}_{c}}+{{A}_{v}})\]

where A_v is the variable part of amplitude. The dispersion coefficients at harmonic URF, which control the coherent components of processes on frequency interval, are the following:

\[CD=A_{c}^{2}/(A_{c}^{2}+A_{v}^{2}/2)\]

for harmonic modulation function F_m and

\[CD=A_{c}^{2}/(A_{c}^{2}+A_{v}^{2}/3)\]

for saw-tooth-shaped modulation function. The modulation frequencies and carrier frequency must be incommensurable here. In [7] illustrates the simultaneous distribution density of URF for coherent function of 0.5 through amplitude-modulated harmonics.

In the third case the coherent function is defined by the modulation index and calculated from the first kind Bessel’s functions of zeros-order [12]. Figure in [7] gives an indication of the simultaneous distribution density of two frequency-modulated harmonics for coherent function of 0.5. With this technique, the result depends only slightly on whether the coherent function is derived by modulation of one or both processes.

 

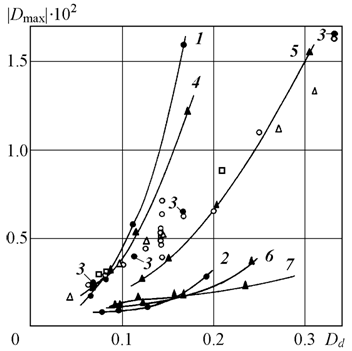
Fig. 2 − Relationship between peak departures from cumulative Gaussian law and discretion degree of spectrum: for a sum of harmonic URF of constant amplitudes (or frequency-modulated URF) distributed uniformly at constant value of spectral density throughout frequency (¡), frequency logarithm (r) and frequency square (o); for a sum of amplitude-modulated harmonic URF with harmonic (l) and saw-tooth-shaped (p) modulation functions at variable modulation degree; 1 – D_m = 0.333;   2 − D_m = 0.23; 3 – D_m = 0.335 [f(A_c) ¹ f(A_v)]; 4 – D_m = 0.25; 5 – D_m = 0.29; 6 – D_m = 0.065; 7 – D_m = 0.21 [f(A_c) ¹ f(A_v)]; 3, 7 – equivalent changing from every amplitude-modulated URF to URF with D_m = 1 and harmonic of incommensurable frequency f

Suppose that we must in addition meet Gaussian distribution. Fig. 2 depicts the relation between the peak departures from cumulative Gaussian law and discretion degree of spectrum. The amplitude modulation at certain modulation degrees is better with this aim in mind [7].

To estimate the life of this structure element we must take life calculations for a set of points of contour and choose the lesser value. In the special case that the processes are symmetric, and have identical manner of spectral densities and distribution laws, the region and the time of crack appearance will correspond to the point with greatest dispersion

\[{{D}_{\Sigma }}=CF_{\sigma }^{2}{{D}_{\sigma }}+CF_{\tau }^{2}{{D}_{\tau }}+2C{{F}_{\sigma }}C{{F}_{\tau }}\sum\limits_{\Delta {{f}_{i}}}{\sqrt{C{{D}_{i}}[\sigma ]{{D}_{\sigma }}C{{D}_{i}}[\tau ]{{D}_{\tau }}}\cos {{\varphi }_{i}}}\]

Here CF_s and CF_t are concentration factors for this point at contour of a hole from nominal normal stress s and nominal shear stress t. Dispersion coefficients CD_i[s] and CD_i[t] depend on the coherent portions of process dispersions on frequency intervals Δf_i, and j_i are displaces in phases between coherent parts of processes conforming to relative phase spectrum [13]. In this case, the critical locations at contour of a hole may be in regions from points with CF_s = Max to points with CF_t = Max within two pairs of opposite angles of p/4.

The products CD_i[s]×CD_i[t] are equal to coherent functions of processes on associated frequency intervals. In the event that we have several processes, these multipliers in pairs form the coherent matrix.

Synthesis techniques of inter-correlated processes of stress and temperature variations are no different from the synthesis techniques of inter-correlated processes of loading. The distinction is in the realization of strain and damage calculation procedures on the time step. In [7] are correlated the experimental and calculated data of life for the sheets with central holes and riveted stringer both under coherent processes and under independent processes of tension and heating. The tests under thermo cyclic loading are performed both under alternative thermal stresses only (with a great static mean load) and under synchronous cyclic load and temperature variations. The range of calculated values of life is consistent with basic errors of load and temperature, whereas the range of experimental values – with true spread of life. Within limits of experimental errors and deflections in the material properties, all test data accord with calculations.

Processes of failure at creep and fatigue are proceeding concurrently but that is determined the longevity which ends firstly. There is needed to estimate interaction of damages of different type and change of structural state of material [14, 15].

Conclusion

The use of kinetic approach, which is based on the physical notions of fracture, for solving strength problems, makes possible the calculation life assessments of structural components under arbitrary temperature-force effects. The presenting of actual random processes as a sum of unit random functions with discrete spectrum solves very simple a problem of reproducing of their interconnection on life estimations of structure elements.

References

1. Petrov M.G., Ravikovich A.I. Deformation and failure of aluminum alloys from the standpoint of the kinetic concept of strength // Journal of Applied Mechanics and Technical Physics. - 2004. - V. 45, No 1. - P. 124-132.
2. Petrov M.G. Rheological properties of materials from the point of view of physical kinetics. // Journal of Applied Mechanics and Technical Physics. – 1998. - V. 39, No 1, - P. 104-112.
3. Петров М.Г. Некоторые структурные модели для описания реологических свойств материалов // Механика композиционных материалов и конструкций. - 2007. - Т. 13, № 2. - С. 191-208.
4. Petrov V.A. Kinetic approach to fracture of solids (III): The statistical features of the time to break (longevity). Homogeneous material. // Phys. Stat. Sol. (b). - 1972. - V. 54, No 1. - P. 369-377.
5. Петров В.А., Башкарев А.Я., Веттегрень В.И. Физические основы прогнозирования долговечности конструкционных материалов. - СПб.: Политехника, 1993. - 475 с.
6. Вентцель В.С., Овчаров Л.А. Теория случайных процессов и её инженерные приложения. - М.: Наука, 1991. - 384 с.
7. Petrov M.G. Simulation of random thermal and loading effects that are taken by aircraft structure // Proceedings of XIII International conference on the methods of aerophysical research. Part I. - Novosibirsk: Publishing House «Parallel», 2007. - P. 165-170.
8. Conle A., Topper T. H. Overstrain effect during variable amplitude service history testing // International Journal of Fatigue. - 1980 - V. 2, No. 3. - P. 130-136.
9. Conle A., Topper T. H. Fatigue service histories: techniques for data collection and history reconstruction. - SAE paper 820093, 1982.
10. 10. Tucker L.E., Bussa S.L. The SAE cumulative fatigue damage test program. Fatigue under complex loading. - SAE, 1977. - P. 1-53.
11. Tucker L.E., Downing S., Camillo L. Accuracy of simplified fatigue prediction methods. - SAE paper 750043, 1975.
12. Анго А. Математика для электро- и радиоинженеров. - М. Наука, 1967. - 780 с.
13. Бендат Дж., Пирсол А. Измерение и анализ случайных процессов. М.: Мир, 1974. – 464 с.
14. Petrov M.G., Ravikovich A.I. Damage accumulation in aluminum alloys under plastic deformation and creep // Journal of Applied Mechanics and Technical Physics. - 2006. V. 47, No 1. - P. 143-151.
15. Petrov M. G. Some methods of analysis and diagnostics of structure and properties of materials produced under various technological processes // Proceedings of XIV International conference on the methods of aerophysical research. Section V. - Novosibirsk: ITAM, 2008. - 1 electron. opt. disc. - Paper No 24.