Insulin level prediction system based on the Brown model for patients with type 1 diabetes mellitus

Математическое моделирование биологических процессов представляет собой сложную многопараметрическую задачу, находящуюся на стыке медицины, биологии и информационных технологий

Существующие системы прогнозирования уровня глюкозы и расчета доз инсулина часто не обладают достаточной точностью, что может приводить к опасным для жизни пациента состояниям — гипогликемической или гипергликемической коме

В последние годы наблюдается смещение исследовательского фокуса от чисто глюкозо-ориентированных предсказательных моделей к методам, напрямую учитывающим и/или оценивающим активный инсулин (Insulin-on-Board, IOB) и параметры дозирования. Так, предложены модельные оцениватели IOB на основе расширенного фильтра Калмана, использующие прямые измерения инсулина для более точной в реальном времени оценки «остаточного» действия введённых доз, что критично для предотвращения гипо- и гипергликемии

Одновременно развиваются клинически ориентированные AI-системы титрования: в рандомизированном исследовании показано, что алгоритм AI способен обеспечивать качество инсулин-терапии, сопоставимое с врачом, что подтверждает клиническую реализуемость интеллектуальных решений в дозировании

Параллельно активно исследуются подходы глубокого обучения: от автоматического расчёта болюсной дозы при «необъявленных» приёмах пищи средствами (Deep Reinforcement Learning, DRL) до трансформерных и мультимодальных архитектур для персонализированного краткосрочного прогноза CGM-сигнала, что улучшает предсказуемость динамики и позволяет учитывать контекст пациента

На этом фоне предлагаемая в статье модификация модели Брауна с адаптивными параметрами и каскадным расчётом статистик занимает нишу легковесных, интерпретируемых и вычислительно экономных предсказателей временных рядов инсулина. В отличие от DL/DRL-подходов, требующих значительных массивов данных и сложной настройки, адаптивное экспоненциальное сглаживание обеспечивает прозрачность и быструю персонализацию, а явная фокусировка на IOB (по аналогии с EKF-оцениванием) делает метод релевантным текущим трендам, при этом создавая основу для гибридизации (например, инициализация/регуляризация параметров по данным из DL-моделей)

Таким образом, новизна данного исследования заключается в модификации модели Брауна за счет адаптивных параметров и каскадного расчета статистических характеристик для заданного числа лагов, что позволяет строить индивидуально адаптирующуюся под конкретного пациента математическую модель регуляции гликемии. Целью работы является разработка и исследование программной системы, реализующей функцию прогнозирования значения инсулина на основе модели Брауна.

В качестве источника данных для исследования использовались значения инсулина, полученные из памяти инсулиновой помпы пациента с сахарным диабетом 1 типа (см. таблицу). Исходный временной ряд состоял из 1182 измерений, проведенных с интервалом в 3±1 минуты. Погрешность измерения значений инсулина составила ±0,001 м.е.

Для анализа и прогнозирования была выбрана модель Брауна — адаптивная модель прогнозирования, основанная на методе экспоненциального сглаживания и позволяющая выделить две основные компоненты временного ряда: уровень и тренд

Для модели первого порядка прогнозируемое значение рассчитывалось по формуле 1:

где:

i — текущее время; i = 1, 2, …, N, или

k — время упреждения; k=1, 2, …, N-1, или

A0, A1 — коэффициенты, поиск которых осуществляется с помощью метода наименьших квадратов

Для модели второго порядка использовалась формула 2:

где:

i — текущее время; i = 1, 2, …, N, или

k — время упреждения; k=1, 2, …, N-1, или

A0, A1, A2 — коэффициенты, поиск которых осуществляется с помощью метода Крамера.

В результате вывода получились следующие формулы для коэффициентов модели (формула 3):

Перед построением моделей был проведен анализ временного ряда. С помощью теста Дики-Фуллера была подтверждена стационарность ряда для всех исследуемых лагов. Анализ линейного тренда для лагов j=1, j=3, j=10 показал его отсутствие (коэффициент детерминации R2<0,3), что обусловило применение теста с константой.

В качестве оценки адекватности модели решено использовать абсолютную и относительную погрешность, вычисляет по формуле 4:

где:

∆ — абсолютная погрешность измерения,

y — значения инсулина, полученное с датчика,

где:

δ — относительная погрешность измерения,

y — значения инсулина, полученное с датчика,

Программная реализация системы была выполнена на языке Python в среде разработки PyCharm с использованием библиотек NumPy, Pandas, OpenPyXL и Tkinter. Программа позволяет загружать данные из Excel-файла, задавать количество лагов, производить каскадный расчет статистических характеристик (математическое ожидание, дисперсия, среднеквадратическое отклонение, минимум, максимум, мода, автоковариация, автокорреляция), каскадно вычислять коэффициенты моделей Брауна, выполнять прогнозирование и сохранять результаты в формате Excel.

Были проведены вычислительные эксперименты для лагов j=1, 3, 7, 10, 20, 30, 40, 60, что соответствует прогнозированию на 3, 9, 21, 30, 60, 90, 120 и 180 минут вперед соответственно. Для каждого лага исследовались статистические характеристики и оценивалась точность прогноза.

Анализ автокорреляционной функции показал, что для малых лагов (j=1, j=3) корреляция является высокой и весьма высокой по шкале Чеддока (от -0,9 до -0,7). С увеличением лага корреляция ослабевала, начиная с 50-го сдвига для j=1 и с 5-9-го сдвига для больших лагов, она классифицировалась как слабая (~0,3 – 0,1) и умеренная (~0,5 – 0,3). Однако на больших сдвигах (например, после 950-го для j=1) наблюдался повторный рост корреляции, что может быть связано с циклическими суточными колебаниями уровня инсулина. Точность прогнозирования оценивалась по средней относительной ошибке. Наилучшие результаты показала модель Брауна первого порядка. Ее средняя относительная ошибка варьировалась от 11,67% (для j=20) до 22,5% (для j=30). Модель второго порядка продемонстрировала признаки переобучения, особенно на малых лагах (j=1, j=3), где ее средняя относительная ошибка достигала высоких значений, что делает ее непригодной для практического использования в данной конфигурации. Для лагов j=7, j=10, j=20, j=30, j=40, j=60 ошибка модели второго порядка была сопоставима или незначительно превышала ошибку модели первого порядка.

Причина лучшей работы модели первого порядка заключается в том, что простая линейная структура позволяет избежать избыточного подстраивания под случайные колебания ряда. Модель второго порядка пыталась аппроксимировать шум как закономерность, что приводило к завышению прогноза и росту ошибки. Таким образом, природа ошибок связана с избыточной чувствительностью более сложной модели к локальным флуктуациям, тогда как модель первого порядка лучше отражает общую динамику процесса.

На рисунке 1 представлен график коэффициента корреляции Пирсона для лага j=1, иллюстрирующий высокую степень зависимости между соседними измерениями при малом временном запаздывании.

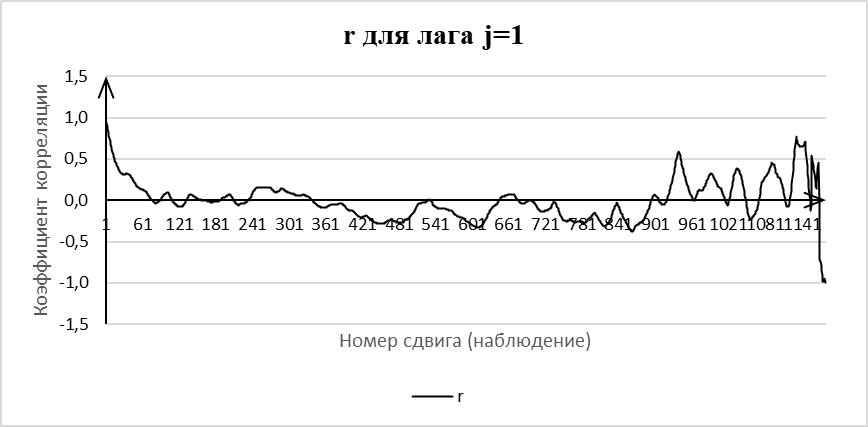
Рисунок 1 - График коэффициента корреляции Пирсона для временного ряда инсулина

Примечание: лаг j=1

DOI:10.60797/IRJ.2025.161.51.2

На рисунке 2 показан пример прогнозирования временного ряда с помощью модели Брауна первого и второго порядка для лага j=20. Видно, что прогнозные значения адекватно следуют общему тренду, однако присутствует заметный разброс ошибки.

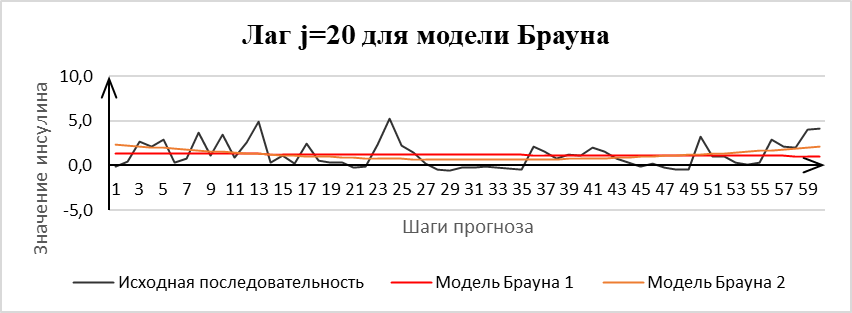
Рисунок 2 - График исходных и прогнозных значений инсулина

Примечание: модель Брауна 1-го и 2-го порядка, лаг j=20

DOI:10.60797/IRJ.2025.161.51.3

В результате работы была разработана и реализована программная система для прогнозирования уровня инсулина на основе модели Брауна. Проведенные вычислительные эксперименты на реальных данных показали, что временной ряд инсулина является стационарным и обладает выраженной автокорреляционной зависимостью на малых лагах. Наилучшая точность прогноза была достигнута с использованием модели Брауна первого порядка для лага j=20 (60 минут), средняя относительная ошибка составила 11,67%. Модель второго порядка склонна к переобучению на данных данной природы и показала неудовлетворительные результаты для краткосрочного прогнозирования.

Перспективы дальнейших исследований связаны с интеграцией в модель дополнительных физиологических параметров (уровень глюкозы, прием углеводов, физическая активность), использованием гибридных моделей (например, сочетание модели Брауна с нейронными сетями), а также проведением клинических испытаний для валидации системы на более обширных выборках данных.