Modelling of Digital Noise Generation
Modelling of Digital Noise Generation
Abstract
The work is dedicated to the analysis of structural models of digital noise generation. The article presents a number of models of digital noise generation as a means of information protection. Structural schemes based on ring oscillators, linear shift registers with feedbacks are presented. As analogues the physically unclonable functions made on the basis of ring pulse generators with delay line on the basis of multiplexers; hybrid generators; on the basis of Box-Muller algorithm; on the basis of ring oscillator with metastable state and a model on the basis of FPGA are given. A description of the methods for evaluating the quality of generated sequences is given, in particular, graphical tests for analysing pseudo-random sequences are specified. The work presents the result of research on the selected structure of the digital noise generator based on ring oscillators. The ring oscillator based random sequence generator synthesizes a signal with a certain frequency. The frequency of the signal in each ring oscillator depends on the signal delay in each inverting element, and may be slightly different in different ring oscillators due to small deviations in the element parameters. The results of graphical tests are demonstrated: histogram of the distribution of a sequence of random numbers; distribution of elements of a sequence of random numbers on a plane; bit-by-bit autocorrelation function of a random series; symbolic autocorrelation function of a random sequence.
1. Введение
Задача получения шумового сигнала с заданными параметрами является актуальной для разработки цифровых систем обработки информации. В зависимости от области применения, требования к шумовому сигналу могут быть разными, например, в радиоэлектронной борьбе может требоваться создание шумовой завесы с определенным спектральным распределением и мощностью, а в криптографии может требоваться создание случайной последовательности с высокой энтропией.
Цифровые источники шума используются в различных областях, включая радиоэлектронную борьбу, где часто используется так называемая «шумовая завеса», в беспроводных коммуникациях они могут использоваться для защиты от перехвата и расшифровки беспроводных сигналов, в криптографии для создания случайных последовательностей, которые используются для шифрования и дешифрования информации и многих других направлениях.
Использование цифровых источников шума имеет ряд преимуществ перед пассивными компонентами, таких как резисторы и диоды. В частности, цифровой генератор шума позволяет получить равномерный спектральный состав шума, имеет более высокую стабильность и контролируемость параметров.
Случайный процесс, получаемый в цифровом генераторе шума, действительно является псевдослучайным, так как основан на алгоритмах генерации случайных чисел. В частности, цифровой генератор шума позволяет получить равномерный спектральный состав шума, имеет более высокую стабильность и контролируемость параметров.
2. Методы и принципы исследования
Рассмотрим структурные модели генерации цифрового шума. Псевдослучайная последовательность (m-последовательность) может формироваться с помощью линейных регистров сдвига с обратными связями (ЛРСОС). Такая последовательность двоичных символов используется для получения шума с равномерной спектральной плотностью в рабочем диапазоне частот, который является «белым» .
Последовательность, генерируемая с помощью ЛРСОС обладает рядом свойств:
1) период последовательности предполагает распределение единиц и нулей в соотношении: количество нулей в последовательности на 1 меньше количества единиц;
2) сумма двух последовательностей, которые являются результатом циклического сдвига исходной m-последовательности, является результатом циклического сдвига исходной последовательности;
3) при скольжении окна шириной r бит вдоль m-последовательности каждая серия из r бит появляется один раз за исключением серии из r нулей.
Для любой m-последовательности свойственно: одна серия из единиц длиной r; одна серий из нулей длиной r-1; одна серия единиц и одна серия нулей длиной r-2; две серии из единиц и две серии из нулей длиной r-3; четыре серии единиц и четыре серии нулей длиной r-4; 2r-3 серий единиц и 2r-3 серий нулей длиной 1.
Другим подходом к получению цифрового шума является использование физически неклонируемых функций . Каждый кольцевой генератор создается на основе уникальных физических свойств, таких как различия в технологическом процессе изготовления или в параметрах материалов. Принцип воспроизведения таких функций основан на неравномерности задержек распространения сигналов по каскадам множества кольцевых генераторов. Изменение задержек невозможно проконтролировать, следовательно, частоты генераторов будут отличаться. Данная особенность и используется для формирования значений функций.
Известны также гибридные генераторы шума, сочетающие цифровой источник первичного шума с прецизионными цифроаналоговыми преобразователями (рисунок 1) .
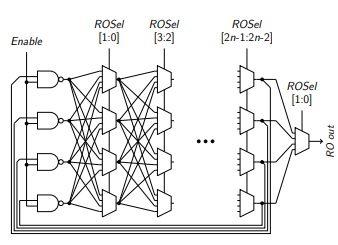
Рисунок 1 - Структура кольцевого генератора импульсов с линией задержки на основе мультиплексоров
Белый шум может быть получен, используя лишь два независимых случайных значения. Пара независимых случайных величин является аргументами для трансцендентных функций, значения которых невозможно вычислить с помощью полиномиальных выражений. Следовательно, для аппаратной реализации потребуется только два ЛРСОС. Результаты вычислений по алгоритму Box-Mueller могут храниться в памяти, а её адресация происходит псевдослучайным образом. Дальнейшая обработка случайных значений подразумевает умножение с накоплением и преобразование интегрированного потока в аналоговую форму. Такие процедуры позволяют сгладить неравномерности Гауссового распределения. Качество такого шума можно оценить, используя функцию плотности вероятности.
В работе в качестве источника шума предложен кольцевой генератор импульсов, способный перейти в метастабильное состояние. Данный метод получения энтропии в системе позволяет увеличить пропускной диапазон генератора случайных чисел при меньшем времени накопления.
Основой такого генератора является инвертор, замкнутый петлёй обратной связи, через переключатель (рисунок 2).
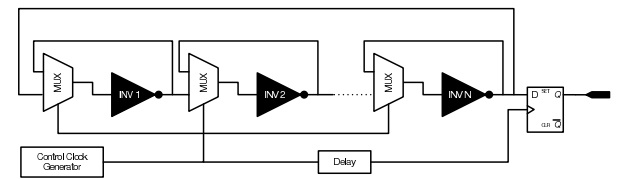
Рисунок 2 - Кольцевой генератор с метастабильным состоянием
В случае, когда переключатель замкнут, инвертор находится в метастабильном состоянии и напряжение на его выходе колеблется вследствие теплового шума. Если из таких элементов состоит кольцевой генератор, то его начальное состояние будет зависеть от энтропии, которая возникает при колебаниях выходного напряжения.
Существуют также способы создания генераторов случайных чисел на базе программируемых логических интегральных схем. Идея состоит в том, чтобы использовать кольцевой генератор импульсов в качестве узла, задающего тактовую частоту. Кроме того, используется так называемый хаотический генератор, состоящий из последовательной цепи инверторов, охваченной обратной связью через элемент «Исключающее ИЛИ». Производительность такого генератора может быть увеличена повышением тактовой частоты, либо добавлением каскадов, соединенных параллельно. Для усиления статистических свойств могут применяться блоки последующей обработки, которые представляют собой ЛРСОС на выходе каждого хаотического генератора , , , .
3. Основные результаты
Анализируя представленные выше модели генерации цифрового шума, и основываясь на субъективном выборе, предлагается принять к рассмотрению модель на основе кольцевого генератора шума, используя особенность метастабильности триггера как источника энтропии в цифровой системе обработки информации.
На основе рассмотренных структурных моделей генерации цифрового шума, предлагается для дальнейшего исследования выбрать собственную структуру генератора цифрового шума на базе кольцевых генераторов (рисунок 3 а).
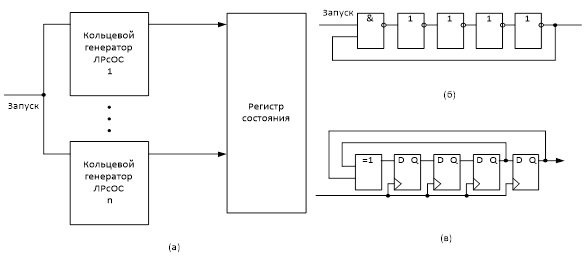
Рисунок 3 - Генератор шума:
а) общая структура генератора цифрового шума; б) кольцевой генератор импульсов; в) ЛРСОС
На основе данных положений выделим две структуры генератора цифрового шума. Первая предполагает в качестве источников шума использовать множество ЛРСОС, состояние которых в дальнейшем фиксируется в регистре, работающем на системной частоте (рис 3, б). Вторая структура использует в качестве источников шума кольцевые генераторы импульсов, обладающие более высокой спектральной плотностью мощности и подверженные влиянию питающего напряжения, температуры, а также технологического разброса параметров кристалла (рисунок 3, в).
В дальнейшем планируется провести исследование статистических свойств подобной структуры генератора с использованием графических тестов анализа псевдослучайных последовательностей.
4. Обсуждение
Реализуем генератор случайной последовательности из шестнадцати кольцевых генераторов с нечётным количеством каскадов от 3 до 33 (Рисунок 3, б), работающих параллельно.
Оценку качества генерируемых последовательностей можно выполнить с помощью набора тестов. Имеется ряд графических тестов, позволяющих провести анализ последовательности:
– тест на равномерность распределения в виде гистограммы, на которой отображаются частоты появления каждого значения;
– тест на автокорреляцию, представляющий собой график автокорреляции, на котором отображается корреляция между каждым значением и его задержанным экземпляром;
– тест на серийность, который используется для проверки наличия серий (последовательностей одинаковых значений) в последовательности. Для этого используется график серийности, на котором отображается количество серий заданной длины в последовательности;
– тест на частоту битов используется для проверки равномерности распределения нулей и единиц в последовательности. Для этого используется график частоты битов, на котором отображается количество нулей и единиц в последовательности;
– тест на длину последовательности использует график длины последовательности, на котором отображается количество вхождений последовательностей заданной длины в сгенерированную последовательность;
– тест на повторение блоков в виде графика повторения блоков, на котором отображается количество повторов каждого блока в последовательности;
– тест на случайность перестановок использует график перестановок, на котором отображается количество циклов в перестановке.
Проект выполнен на отладочной плате Sipeed Tang Nano 9K с FPGA Gowin GW1NR-LV9QN88PC6/I5, язык описания аппаратуры Verilog HDL.
Каждую секунду состояние генератора фиксируется в регистре и отправляется в последовательный порт компьютера (рисунок 4).

Рисунок 4 - Состояние генератора
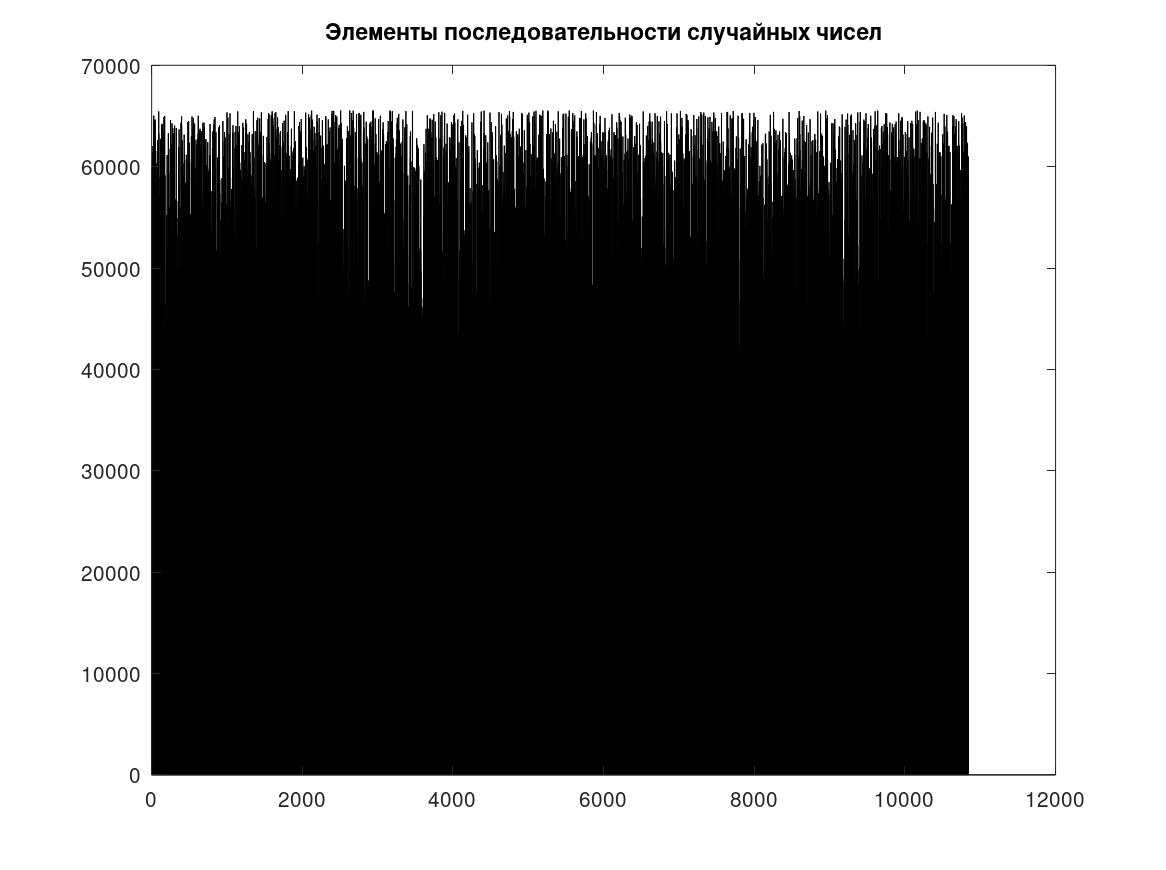
Рисунок 5 - Графические характеристики качества случайной последовательности — элементы последовательности случайных чисел
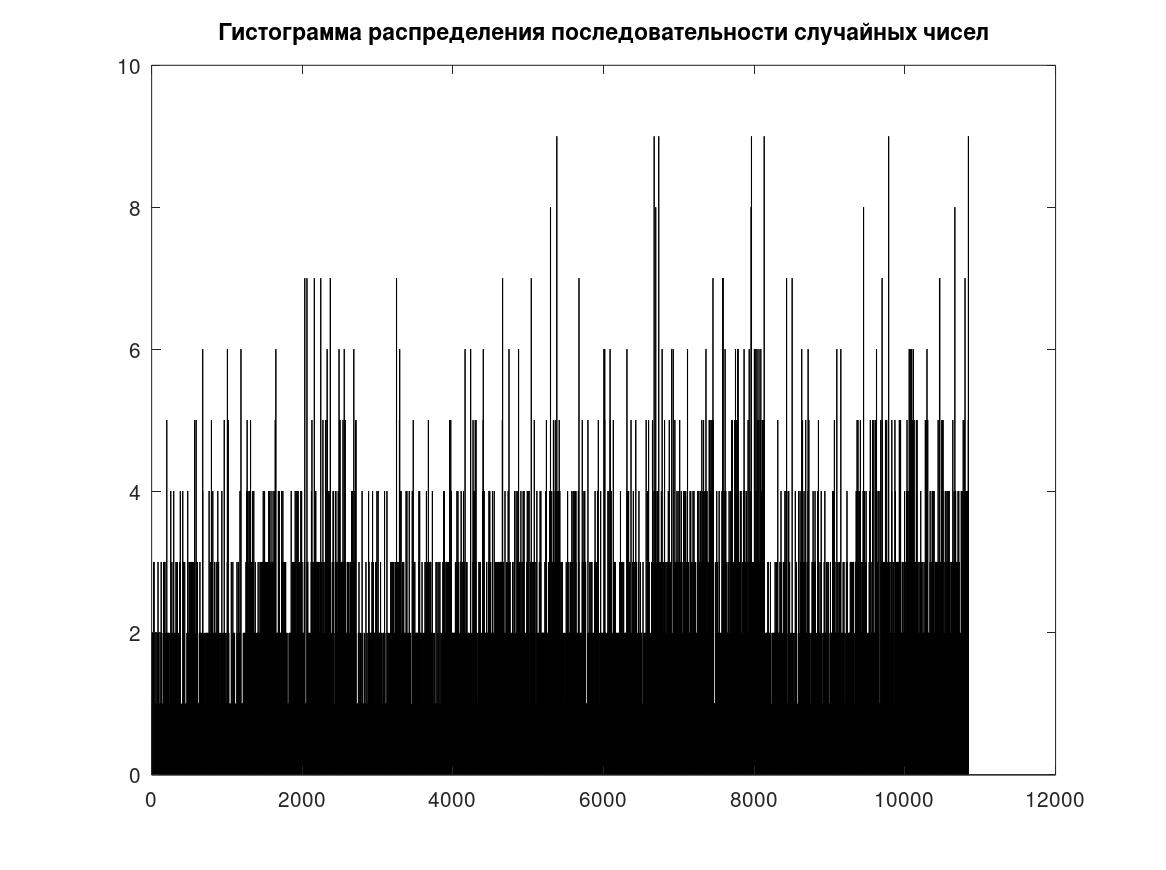
Рисунок 6 - Графические характеристики качества случайной последовательности — гистограмма распределения последовательности случайных чисел
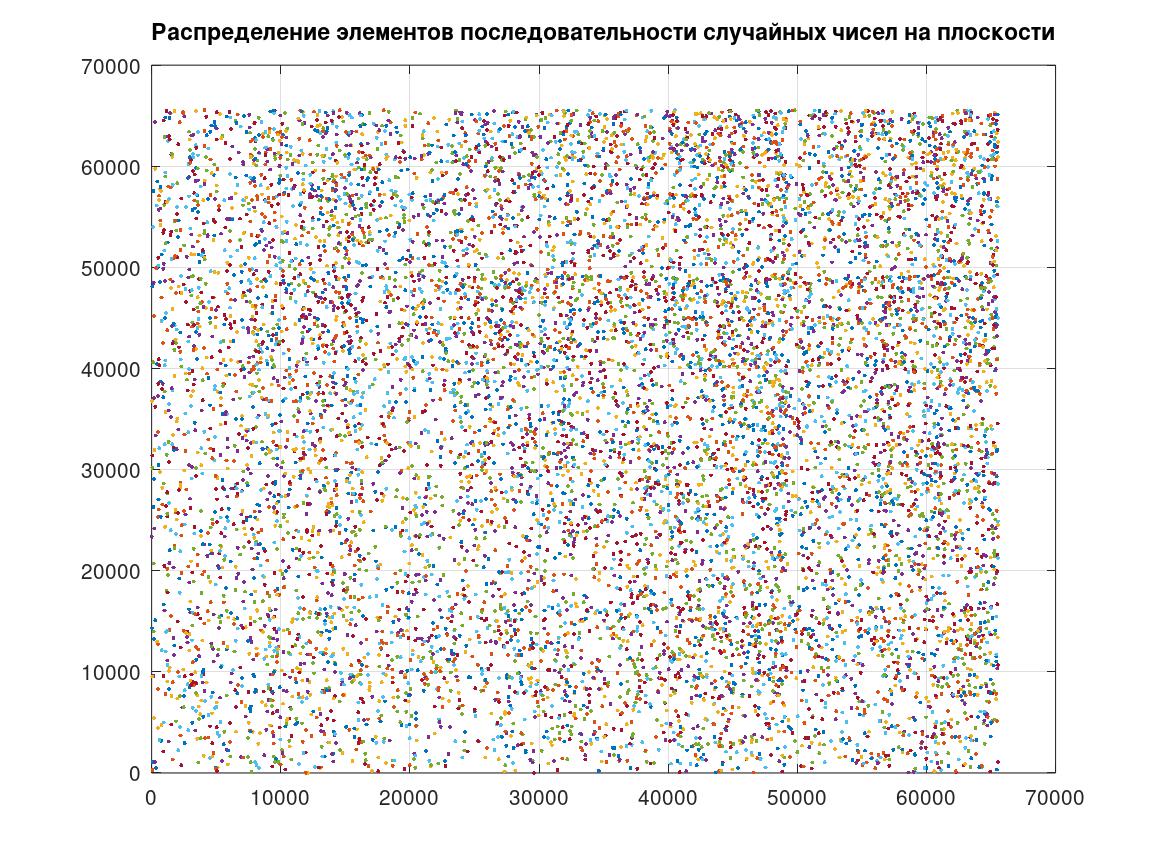
Рисунок 7 - Графические характеристики качества случайной последовательности — распределение элементов последовательности случайных чисел на плоскости

Рисунок 8 - Пиксельное изображение случайной последовательности
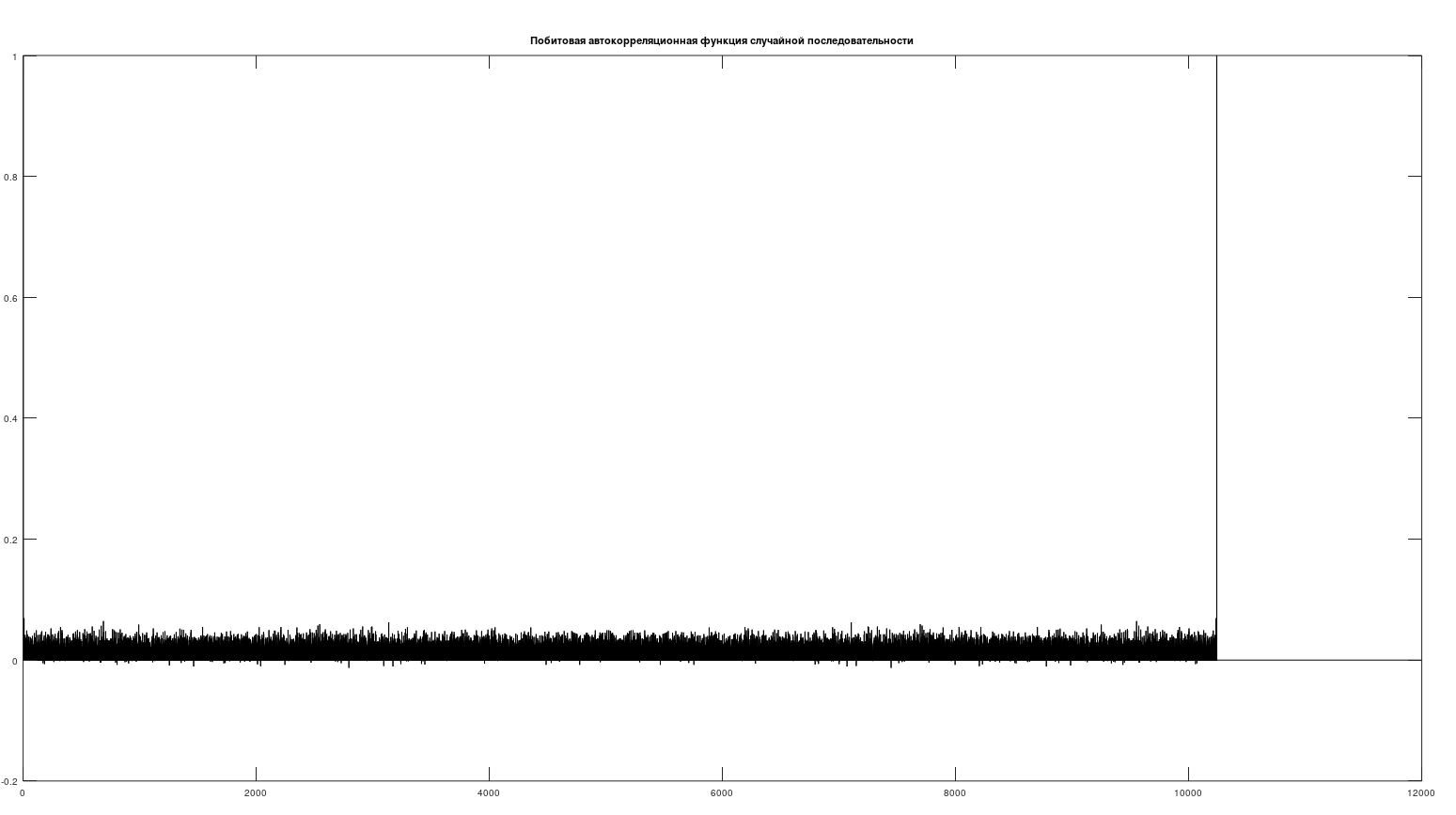
Рисунок 9 - Побитовая автокорреляционная функция случайной последовательности
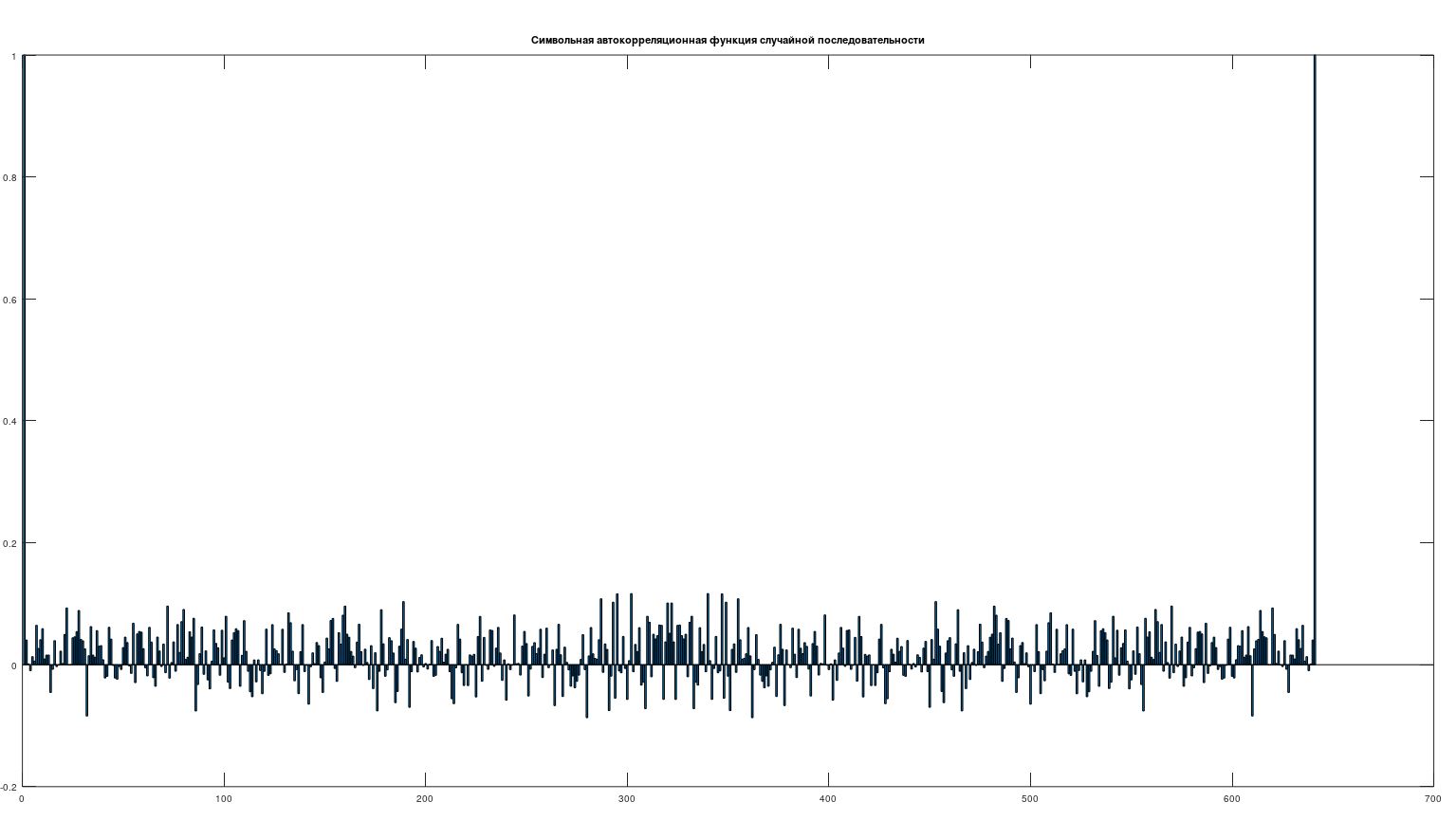
Рисунок 10 - Символьная автокорреляционная функция случайной последовательности
5. Заключение
Исходя из анализа результатов исследования видно, что выбранная структура генератора цифрового шума формирует случайную последовательность и может быть использована для задач подобного направления. В дальнейшем исследование может быть дополнено другими методами анализа. Например, для повышения безопасности генераторов цифрового шума на основе ЛРСОС могут использоваться такие методы, как добавление шума к начальному состоянию регистра, использование нескольких ЛРСОС с разными начальными состояниями и обратной связью, а также применение криптографических преобразований к выходной последовательности.
