DEVELOPMENT OF THE ALGORITHM FOR CONSTRUCTING INDIVIDUAL TRAJECTORY OF STUDENT

Корнева А.В.¹, Соловьева Ю.А.², Корнев Е.С.³

¹ Кандидат технических наук, ²Кандидат технических наук, ³Кандидат технических наук, Сибирский государственный индустриальный университет

РАЗРАБОТКА АЛГОРИТМА ПОСТРОЕНИЯ ИНДИВИДУАЛЬНОЙ ТРАЕКТОРИИ РАЗВИТИЯ УЧАЩЕГОСЯ

Аннотация

В статье рассмотрено – разработка алгоритма построения и корректировки индивидуальной траектории развития учащегося с учетом начального уровня знаний и значения функции влияния начальных условий на продолжительность обучения. Для количественной оценки эффективности обучения была построена функция влияния начальных условий на продолжительность освоения дисциплины.

Ключевые слова: алгоритм, индивидуальная траектория, построение индивидуальной траектории  

Korneva A.V.¹, Solovieva J.A.², Kornev E.S.³

¹ Candidate of Technical Sciences, ²Candidate of Technical Sciences, ³Candidate of Technical Sciences, Siberian State Industrial University

DEVELOPMENT OF THE ALGORITHM FOR CONSTRUCTING INDIVIDUAL TRAJECTORY OF STUDENT

Abstract

The article considers the development of an algorithm for constructing and adjusting the trajectory of the individual trajectory of student, taking into account the initial level of knowledge and values of the influence of initial conditions on the duration of the training. To quantify the effectiveness of the training was constructed influence function of the initial conditions on the duration of the development of the discipline.

Keywords: automation, business process, industry.

Темп развития современного мира приводит к росту потребности людей в новой информации для продуктивной профессиональной деятельности. Все это отразилось на системе общего среднего, специального и, особенно,  высшего профессионального образования. От современных специалистов требуется способность мобильно и гибко реагировать на инновационные продукты, быстро адаптироваться к изменяющимся условиям труда. Особую актуальность и ценность приобретает развитие у студентов в процессе обучения умение самостоятельной учебной деятельности. Развитие этих навыков следует осуществлять уже при подготовке к обучению в вузе, так как это позволить не только увеличить адаптированность учащегося к условиям обучения в вузе, но и существенно повысить уровень образовательной подготовки.

При разработке алгоритма построения индивидуальной траектории первоначально необходимо определить необходимый уровень знаний учащегося подготовки по базовым дисциплинам для успешного освоения программ ВПО по определенному направлению обучения в ВУЗе.

Начальные условия, такие как период обучения, частота посещения занятий, количество тем в изучаемой дисциплине и др. оказывают существенное влияния на продолжительность освоения дисциплины учащимся. Эти факторы можно учесть в алгоритме посредством линейной функции, значение которой будут использоваться при построении индивидуальной траектории.

Корректировку индивидуальной траектории развития учащегося необходимо осуществлять на каждом шаге итерационного процесса посредством минимизировать ее отклонение от базовой. При численном решении задачи минимизации для учета ограничений в алгоритме построения индивидуальной траектории целесообразно использовать метод штрафных функций.

На начальном этапе алгоритма определяется базовая траектория подготовки учащихся, для которой используются усредненные статистические данные приемных компаний ВУЗов за пятилетний период.

Для учета влияния начальных условий на продолжительность освоения дисциплины предлагается функция (P_осв), которая позволит количественно оценить эффективность обучения вида

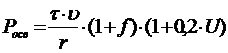, (1)

где r – количество тем для изучения, τ – возможный период обучения,  – частота посещения занятий, f – финансовая обеспеченность, U - возможность удаленного доступа к ресурсам образовательного процесса.

На основе значения функции влияния начальных условий строится индивидуальная траектория подготовки учащегося. Начальная точка траектории принимается равной начальному уровню знаний старшеклассника Y_нач. Исходя из значения функции продолжительности, определяется конечная точка траектории по формуле

,      (2)

где P_осв – значение функции влияния начальных условий на продолжительность освоения дисциплины, k – коэффициент продолжительности обучения, k =0,25 ÷0,32.

Для минимизации отклонения индивидуальной траектории от базовой решается задача численного моделирования.

Дано: значения базовой траектории Q_баз, значения индивидуальной траектории по каждой из тем x₁,x₂,…,x_r.

Начальные условия: возможный период обучения (τ), частота посещения занятий (), финансовая обеспеченность (f), возможность удаленного доступа к ресурсам образовательного процесса (U), количество тем в дисциплине (r), точность вычислений (ε).

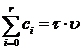Ограничение: , где c₀,с₁,…,с_r – количество часов по каждой теме.

Требуется: подобрать такие значения постоянных числовых параметров с₀,с₁,…,с_r, чтобы минимизировать разницу между уровнем освоения дисциплины базовой траектории и индивидуальной, определяемой значениями функции  в зависимости от уровня освоения тем, входящих в дисциплину (x₁,x₂,…,x_r)

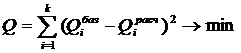.       (3) Решение: зависимость Q_расч для i-го измерения можно записать в виде 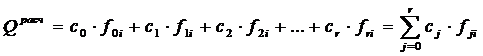,      (4)

где f_ji – значение j-ой функции при значениях независимых переменных в i-м эксперименте.

После подстановки выражения (4) в сумму квадратов невязок формула (3) с учетом штрафной функции будет иметь вид

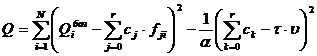, (5) где α – настроечный параметр в методе штрафных функций, .

Для нахождения минимума функции Q требуется одновременное равенство нулю частных производных по параметрам c₀,c₁,…,c_r:

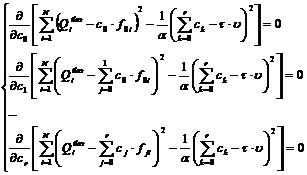    (6)

Значения коэффициентов c₀,c₁,…,c_r определяются посредством решения системы линейных алгебраических уравнений и осуществления предельного перехода при .

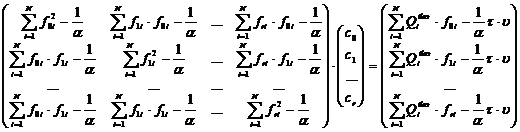 (7)  

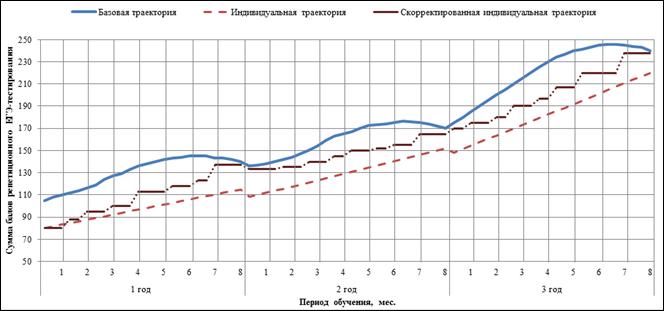
Рисунок 1 – Пример построения и корректировки индивидуальной траектории обучения

 

Таким образом, был разработан алгоритм построения индивидуальной траектории подготовки учащегося с учетом функции влияния начальных условий на продолжительность освоения дисциплины, позволяющий посредством численного моделирования поэтапно минимизировать отклонения индивидуальной траектории от базовой с применением метода штрафных функций для учета ограничений. Кроме того, установлено, что многоуровневая корректировка индивидуальной траектории развития учащегося на протяжении всего периода обучения позволяет существенно повысить степень освоения дисциплины.

Литература

1. Корнева А.В. Разработка математической модели оценки и учета личностных параметров при довузовской подготовке учащихся [Текст] / А.В. Корнева, Л.Д. Павлова , Ю.А. Соловьева // Научное обозрение№ 8. – М, 2015.- С. 225-230.
2. Соловьева А.В. Компьютерное моделирование многоуровневой системы подготовки учащихся к освоению программ высшего профессионального образования [Текст]: Дис... канд. тех. наук. - Новокузнецк, 2013. – 142.
3. Соловьева А.В. Компьютерное моделирование многоуровневой системы подготовки учащихся к освоению программ высшего профессионального образования [Текст]: Автореф. дис... канд. тех. наук. - Новокузнецк, 2013. – 19
4. Соловьева А.В. Разработка программного комплекса многоуровневой системы подготовки абитуриентов/А.В. Соловьева, Л.Д. Павлова, Ю.А. Соловьева//Телематика'2013: сб. науч. ст. -СПб: СПбГУ ИТМО, 2013. -С. 215-220.
5. Соловьева А. В.Организационно-функциональная система построения индивидуальной траектории подготовки конкурентоспособного абитуриента [Текст] / А.В. Соловьева, Л.Д. Павлова , Ю.А. Соловьева  // Педагогический профессионализм в образовании: сб. науч. статей. - Новосибирск: НГПУ, 2012. -С. 390-397.
6. Соловьева А. В. [Текст] / А.В. Соловьева, Ю.А. Соловьева Построение индивидуальной траектории карьерного развития на этапе довузовской подготовки//Телематика’2011: сб. научных статей. -СПб.: СПбГУ ИТМО, 2011. -С. 212-214.

References

1. Korneva A.V. Development of mathematical model for assessment and management of personal parameters in pre-university preparation of students [Text] / A.V. Korneva, L.D. Pavlova, J.A. Solovieva // Scientific Review № 8. - M, 2015.- pp 225-230.
2. SolovievаV. Computer simulation of multi-level system of preparation of students to development programs of higher education [Text]: Dis ... Cand. tech. Sciences. - Novokuznetsk, 2013. - 142.
3. Solovieva A.V. Computer simulation of multi-level system of preparation of students to development programs of higher education [Text]: Author. dis ... cand. tech. - Novokuznetsk, 2013. - 19
4. Solovieva A.V. Development of the program complex multi-level system of training students / A.V. Solovieva, L.D. Pavlova, J.A. Solovieva // Telematika'2013: Sat. scientific. SPb: ITMO, 2013. -C. 215-220.
5. SolovievаV. Organizational and functional system of construction of individual trajectory of training competitive entrant [Text] / A.V. Solovieva, L.D. Pavlova, J.A. Solovieva // Pedagogical professionalism in education: Sat. scientific. articles. - Novosibirsk: NSPU, 2012. -C. 390-397.
6. Solovieva A.V. [Text] / A.V. Solovieva, J.A. Solovieva Building individual trajectory of career development at the stage of preliminary training // Telematika'2011: Sat. scientific articles. SPb .: ITMO, 2011. -C. 212-214.