THE METHOD OF SECOND-ORDER CALIBRATION AND ERROR CORRECTION FOR VECTOR NETWORK ANALYZER MEASUREMENTS

Савин А.А.

Кандидат технических наук, Томский государственный университет систем управления и радиоэлектроники

Работа выполнена при поддержке гранта Президента Российской Федерации № МК-3107.2015.8

МЕТОД ДОПОЛНИТЕЛЬНОЙ КАЛИБРОВКИ И КОРРЕКЦИИ ИЗМЕРЕНИЙ ВЕКТОРНОГО АНАЛИЗАТОРА ЦЕПЕЙ

Аннотация

В статье рассмотрено – применение специального метода калибровки для увеличения точности векторного анализатора цепей, частотно-временная модель калиброванного анализатора, которая является основой дополнительной калибровки и коррекции измерений, и порядок обработки верификационных измерений при помощи алгоритма фильтра Калмана.

Ключевые слова: векторный анализатор цепей, калибровка, коррекция верификация.

 

Savin A.A.

PhD in Engineering, Tomsk State University of Control Systems and Radioelectronics

THE METHOD OF SECOND-ORDER CALIBRATION AND ERROR CORRECTION FOR VECTOR NETWORK ANALYZER MEASUREMENTS

Abstract

The article considers applying of special calibration method to increase the accuracy of the vector network analyzer, frequency-time domain model of the calibrated analyzer that is the basis of the second-order calibration and correction, processing order of measurements using unscented Kalman filter.

Keywords: vector network analyzer, calibration, correction, verification.

 

Векторные анализаторы цепей (ВАЦ) предназначены для измерения комплексных коэффициентов передачи и отражения (S-параметров) различных СВЧ устройств. Порядок работы с прибором предполагает его калибровку, необходимую для исключения (математической коррекции) систематической погрешности измерений. В зависимости от качества калибровки, даже калиброванный прибор может содержать неисключенные составляющие систематической погрешности (эффективные параметры). Метод дополнительной калибровки и коррекции измерений ВАЦ предназначен для раздельного оценивания каждого эффективного параметра согласно признанной модели погрешностей прибора в любой среде распространения сигнала (коаксиальной, волноводной или копланарной).

Метод основан на обработке измеренных S-параметров прецизионной линии передачи в следующих режимах: на проход, то есть при подключении линии одновременно к двум измерительным портам прибора; на отражение для каждого измерительного порта отдельно, то есть при подключении короткозамкнутой линии или линии в режиме холостого хода к измерительному порту.

Обработка измерений предполагает совместное оценивание эффективных параметров калиброванного ВАЦ во всей или ограниченной полосе частот прибора. Алгоритм совместного оценивания основан на частотно-временной модели измерений. Каждый эффективный параметр локализован во временной области и его частотные свойства задаются ограниченным набором комплексных отсчетов. Комплекснозначные отсчеты для каждого эффективного параметра располагаются в полосе частот работы прибора (от начальной частоты f_Start до конечной частоты f_End) в сетке с интервалом Δf по частоте. Для расчета Δf используется соотношение:

Δf  = v / (2L),

где v – скорость распространения зондирующего сигнала прибора в среде измерений; L – длина верификационной линии.

Измерения линии передачи в описанных выше режимах должны быть выполнены с шагом по частоте, который меньше Δf более чем в два раза. При расчете частотной характеристики каждого эффективного параметра на произвольной частоте измерений используется интерполяция кубическими сплайнами. На Рис. 1 показана частотно-временная модель калиброванного ВАЦ при тестировании линии с короткозамкнутым или открытым портом.

 

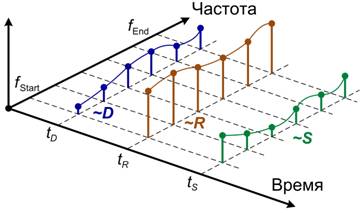
Рис. 1 - Частотно-временная модель калиброванного ВАЦ при тестировании линии с короткозамкнутым или открытым портом

  Для примера, на Рис. 1 каждый эффективный параметр описан набором из 6 отсчетов. При использовании интерполяции кубическими сплайнами требуется минимум 3 отсчета. На Рис. 2 показана частотно-временная модель калиброванного ВАЦ при тестировании линии, которая подключена к двум портам прибора одновременно. Слева на Рис. 2 показана модель для измерений коэффициента отражения, справа – коэффициента передачи.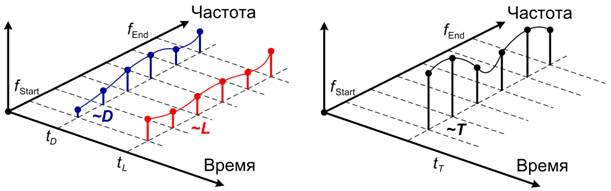  

Рис. 2 - Частотно-временная модель калиброванного ВАЦ при тестировании линии на проход

 

Количество эффективных параметров ВАЦ, который содержит два измерительных порта, равно 10 [1]. Это следующие параметры: направленность (обозначена D на Рис. 1 и 2) для каждого порта; трекинг тракта отраженных сигналов (обозначен R на Рис. 1) для каждого порта; рассогласование порта в режиме источника (обозначено S на Рис. 1) для каждого порта; рассогласование порта в режиме приемника (обозначено L на Рис. 2) для каждого порта; трекинг передачи из первого порта во второй и из второго порта в первый (обозначен T на Рис. 2). Переменной t с нижним индексом обозначено положение на оси времени соответствующего эффективного параметра, которое зависит от длины верификационной линии: t_D = 0; t_R = 2L / v; t_S = 4L / v; t_L = 2L / v; t_T = L / v.

Измеренный коэффициент отражения при тестировании линии в коротким замыканием или холостым ходом (КО₁) можно записать в виде:

КО₁ = D + R·δ²·Γ + S·R·(δ²·Γ)²,

где δ – известный коэффициент передачи линии, определяющий положение эффективного параметра на оси времени; Γ – известный коэффициент отражения короткозамкнутой нагрузки или нагрузки холостого хода. Переменные, входящие в выражение для КО₁, определены для всех точек по частоте, в которых выполнены измерения.

Измеренный коэффициент отражения при тестировании линии на проход (КО₂) можно записать в виде:

КО₂ = D + L·R·δ²,

Измеренный коэффициент передачи при тестировании линии на проход (КП) можно записать в виде:

КП = T·δ,

Переменные, входящие в выражение для КО₂ и КП, определены для всех точек по частоте, в которых выполнены измерения.

В качестве алгоритма одновременной обработки всех измерений (КО₁ для всех измерительных портов, КО₂ и КП для каждой пары измерительных портов) и оценивания эффективных параметров использован известный алгоритм UKF (unscented Kalman Filter) [2]. Применение алгоритма UKF, который использует численную процедуру расчета среднего и ковариационной матрицы, позволяет эффективно  решить задачу оценивания при наличии громоздких выражений, определяющих связь наблюдаемых сигналов и вектора состояния. Вектор состояния содержит действительные и мнимые части отсчетов всех эффективных параметров прибора. Инициализация алгоритма заключается в задании начальных значений вектора состояния (начального приближения или начальной оценки) и ковариационной матрицы погрешности начальной оценки. Начальное приближение для вектора состояния определено следующими свойствами: действительные значения составляющих высокого уровня (трекинги передачи и отражения) равны 1; мнимые значения составляющих высокого уровня равны 0; действительные и мнимые значения параметров низкого уровня (направленности и рассогласования) равны 0. Ковариационная матрица имеет диагональный вид, дисперсии начальных оценок принимаются равными 0.1². После инициализации на вход алгоритма рекурсивно при увеличении частоты начинают поступать измерения, а на выходе фильтра формируются оценки вектора состояния модели измерительной системы в соответствии с математическим аппаратом алгоритма UKF [2]. По мере поступления и обработки измерений точность оценок возрастает. После обработки всех отсчетов измерений достигается максимальная точность оценки вектора состояния. Итоговая оценка используется для расчета эффективных параметров ВАЦ путем применения интерполяции кубическими сплайнами.

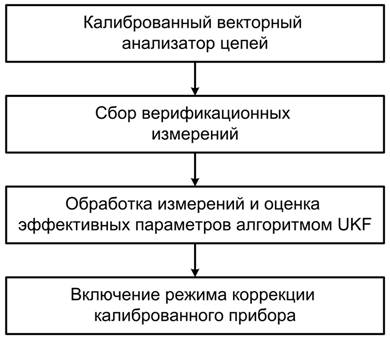
Для увеличения точности измерений S-параметров исследуемых устройств реализована векторная коррекция второго уровня, использующая результаты оценки комплексных параметров и известные [3] формулы исключения систематической погрешности. Полная структурная схема реализации метода дополнительной калибровки и коррекции измерений ВАЦ показана на Рис. 3.

 

Рис. 3 - Структурная схема метода

 

Рассмотренный подход позволяет снизить амплитуду эффективных параметров низкого уровня (D, S, L) примерно на 10 дБ (с минус 35-40 дБ до минус 45-50 дБ) и высокого уровня (R, T) примерно в 5 раз (с 0.05 до 0.01 дБ) в среднем для различных измерительных установок.

Литература

1. Savin A. A. Estimation of Complex Residual Errors of Calibrated Two-Port Vector Network Analyzer / A. A. Savin, V. G. Guba, A. Rumiantsev, B. D. Maxson // Proceedings of the 83rd ARFTG Microwave Measurement Conference. – Tampa, USA, 2014. – P. 1-4.
2. Julier S. J. Unscented filtering and nonlinear estimation / S. J. Julier, J. K. Uhlmann // Proceedings of the IEEE. – 2014. – Vol. 92, No. 3. – P. 401-422.
3. Губа В. Г. Классификация и анализ методов калибровки векторных анализаторов цепей/ В. Г. Губа, А. А. Ладур, А. А. Савин // Доклады ТУСУРа. – 2011. – № 2(24), ч. 1. – С. 149-155.

References

1. Savin A. A. Estimation of Complex Residual Errors of Calibrated Two-Port Vector Network Analyzer / A. A. Savin, V. G. Guba, A. Rumiantsev, B. D. Maxson // Proceedings of the 83rd ARFTG Microwave Measurement Conference. – Tampa, USA, 2014. – P. 1-4.
2. Julier S. J. Unscented filtering and nonlinear estimation / S. J. Julier, J. K. Uhlmann // Proceedings of the IEEE. – 2014. – Vol. 92, No. 3. – P. 401-422.
3. Guba V. G. Classification and analysis of vector network analyzer calibration methods / V. G. Guba, A. A. Ladur, A. A. Savin // Reports of TUSUR – 2011. – № 2(24), part 1. – P. 149-155.