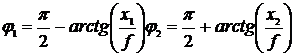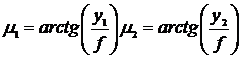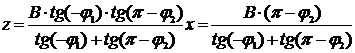CONTROL OF ANGULAR POSITIONS OF STRUCTURAL ELEMENTS WITH A LASER MEASURING SYSTEMS

Сазонникова Н.А.¹, Нонин А.С.², Ткаченко А.С.³, Вобликов Д.Н.⁴

¹Кандидат технических наук, доцент, ^2,3,4 Аспирант, Самарский государственный аэрокосмический университет имени академика С.П. Королева (Национальный исследовательский университет)

КОНТРОЛЬ УГЛОВОГО ПОЛОЖЕНИЯ ЭЛЕМЕНТОВ КОНСТРУКЦИЙ С ПОМОЩЬЮ ЛАЗЕРНЫХ ИЗМЕРИТЕЛЬНЫХ СИСТЕМ

Аннотация

С целью совершенствования контроля положений деталей при сборке и эксплуатации разработана лазерная измерительная система контроля углового положения элементов конструкции. Реализована малогабаритная углоизмерительная система с высокой точностью измерения (погрешность ≤2ʺ) при дистанции между объектом контроля и автоколлиматором до 20 м и диапазоне измерения (10…12ʹ). Задача решена методом "прямой угловой засечки". В результате анализа выявлена погрешность измерения координат центра изображения на ПЗС-матрице измерительного прибора.

Ключевые слова: лазерные измерительные системы, угловое положение, элементы конструкции.

 

Sazonnikova N.A.¹, Nonin A.S.², Tkachenko A.S.³, Voblikov D.N.⁴

¹PhD in Engineering, associate professor, ^2,3,4 Postgraduate student, Samara State Aerospace University

CONTROL OF ANGULAR POSITIONS OF STRUCTURAL ELEMENTS WITH A LASER MEASURING SYSTEMS

Abstract

To improve the monitoring of provisions of parts during assembly and subsequent operation the laser measuring system is designed to control the angular position of the structure. The small-sized measuring rotary system providing high accuracy (error ≤ 2ʺ) when significant working distance between the test object and the autocollimator up to 20 m and a relatively wide measurement range (10...12ʹ) is realized. The method of "straight angled serifs" was constructed to solve this problem. As a result of the analysis the measuring error of co-ordinates of center of the image on an instrument CCD matrix is revealed.

Keywords: laser measuring systems, the angular position, structural elements

 

Метрологическое обеспечение многих измерительных задач производственной и научной деятельности при создании элементов конструкций летательных ап­паратов и двигателей предусматривает измерение пространственного положения объектов контроля относительно единой жёсткой базы в процессе их перемещения. Совершенствование технологий изготов­ления и современных средств производства летательных аппаратов и двигателей требует точного контроля положений де­талей при сборке, заключительных опера­циях и последующей эксплуатации [1-5].

Методику измерения пространст­венного положения элементов конструк­ции рассмотрим на примере системы из­мерения деформаций элементов посадоч­ных мест под чувствительные элементы  системы управления движением леталь­ного аппарата (ЧЭ СУД) (рис. 1).

Вес и температура, действующие на элементы конструкции, вызывают дефор­мацию зеркал, изменение позиции и ли­нейный сдвиг каждой из плоскостей зер­кал относительного заданного положения. Для компенсации этих воздействий необ­ходимо реализовать систему для измере­ния отклонения посадочных поверхностей от установленного номинала [5].

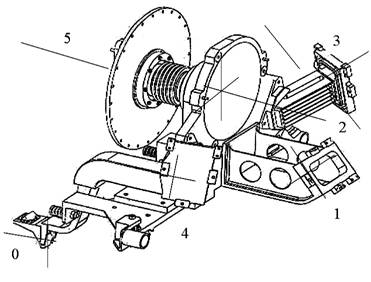
Рисунок 1 – Общий вид конструкции платформы с посадочными местами под ЧЭ СУД: 0 – узел подвески; 1,3,4– места установки зеркал; 2, 5 –вращающиеся плоские зеркала.

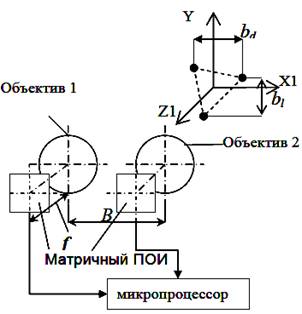
Рисунок 2 – Обобщённая структурная схема оптико-электронной системы, работающей по методу триангуляции

Для контроля углового положения крупногабаритных конструкций эффек­тивны оптико-электронные измеритель­ные системы. Применительно к постав­ленной задаче необходима реализация ма­логабаритной углоизмерительной сис­темы, обеспечивающей высокую точность измерения (погрешность не более 1,5…2ʹʹ) при значительной рабочей дис­танции между объектом контроля и авто­коллиматором (до 20 м) и относительно широком диапазоне измерения (10…12ʹ).

Чувствительность измерения в ОЭС контроля  углового положения элементов конструкции обоих видов по дальности и угловым координатам прямо пропорциональна произведению базового расстояния между контрольными точками объекта (для ОЭС, работающей по методу «угловой засечки» – между центрами апертур объективов двух приемных каналов) на фокусное расстояние объектива [4,5].

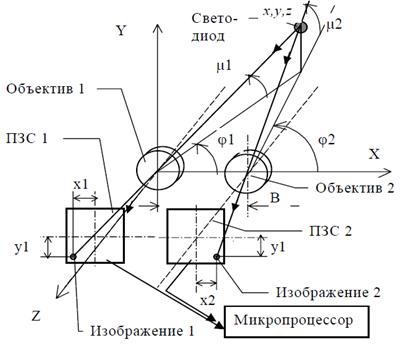
Измерительный канал реализует триангуляционный метод. В соответствии с методом каждая видеокамера измеряет углы визирования лазерного диода, рас­положенного в контрольной точке. Изме­ряются углы визирования в горизонталь­ной и вертикальной плоскостях. Для этого ПЗС-матрицы, расположенные в фокаль­ных плоскостях объективов видеокамер, измеряют по две координаты изображе­ний в горизонтальной и вертикальных плоскостях изображений светодиода со­ответственно (рис. 3).

При решении задачи автоматизиро­ванного контроля положения с объектом связываются визирные цели, фиксирую­щие три и более его контрольных точки. Изображения визирных целей регистри­руются оптико-электронным измеритель­ным преобразователем, включающем в общем случае несколько измерительных каналов, с отдельными анализаторами на основе матричных фотоприемников, и с последующей компьютерной (микропро­цессорной) обработкой видеокадра. При этом предварительная обработка измери­тельной информации может осуществ­ляться в непосредственной близости от анализатора, что увеличивает помехоза­щищённость системы в целом и исклю­чает избыточность информации.

В ОЭС, работающей по методу «угловой засечкой» углы визирования трёх (или более) визирных целей объекта из­меряются двумя видеосистемами, каждая из которых включает матричный приём­ник оптического излучения (ПОИ) (рис. 2). Обработка видеокадров выполняется микропроцессором.

Угловые поля видеосистем перекры­ваются, обеспечивая визирование контро­лируемого объекта, центры объективов видеосистем расположены на известном базовом расстоянии B.

Выполнен теоретический анализ чувствительности ОЭС двух видов к из­мерению линейных и угловых координат.

В частности, при условии измери­тельной задачи, когда система работает на дальнем участки дистанции, L >> B, L>> b_l ,b_d и одной измеряемой координате, чувствительность измерения ОЭС «угло­вой засечки» смещений x,y и дистанции L до объекта определяются выражениями: [3]

,  (1)

.  (2)

Выражения (1),(2) справедливы и для ОЭС метода триангуляции (МТ) «об­ратной угловой засечки» при замене B на b_d. Чувствительность к углам поворота для ОЭС МТ «обратной угловой засечки» определяется выражением

.   (3)

Выражение (3) определяет чувстви­тельность измерения поворота Θ₃ при b = b_d и измерения поворотов Θ₁, Θ₂ при b = b_l.

В ОЭС МТ «угловой засечки» вели­чина b базы между визирными целями не известна заранее, а определяется в про­цессе измерения линейных координат, что определяет потенциально большую по­грешность измерения углов поворота по сравнению с ОЭС МТ «обратной угловой засечки».

Рисунок 3 – Принцип работы прибора по методу «угловой засечки»

Углы визирования и координаты контрольной точки определяются сле­дующими соотношениями:

,   (4)

,    (5)

,   (6)

где , f - фокусное расстояние объектива, В – базовое расстояние между осями видео­камер.

Контроль поверхности площадок проходит в два этапа. На первом – контроль положения посадочных мест проводится без технологических нагрузок. На втором этапе контроль посадочных мест проводится после проведения испытаний. Отражающие зеркала от смещений вдоль оптической оси и от поперечных смеще­ний предохраняют металлические пластины, установленные на площадках.

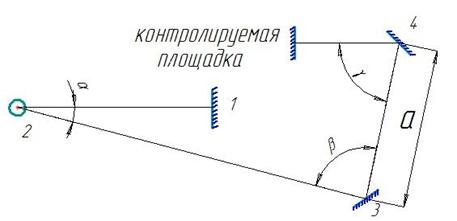
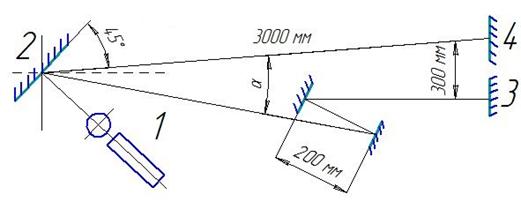
Описанный ниже способ позволяет вы­явить оптическим способом стабильность положения посадочных площадок под чувствительные элементы и оценить воз­действие внешней среды. На рис. 4 и 5 показаны оптические схемы измерений стабильности положения посадочных мест под чувствительные элементы. На рис. 5 представлен общий вид конструкции с посадочными местами под ЧЭ СУД.

В первом случае на рис. 4 приво­дится оптическая схема для определения отклонений площадки чувствительных элементов. Углы β и γ  задаются из усло­вия, что зеркала на базовой и измеряемой поверхности должны устанавливаться строго перпендикулярно оптической оси измерительного прибора 2 (например, те­лекамера). Угол a - находится как α = β  - γ . В данной схеме лазерный излучатель устанавливается на теодолите и необхо­дим для определения точки пересечения опорной и измеряемой оси.

Рисунок 4 – Оптическая система для определения отклонений площадок конструкции подвески чувст­вительных элементов: 1-базовая площадка, 2-измерительный прибор, 3, 4-зеркала для определения места пересечения оп­тических осей, 5-исследуемая площадка

Рисунок 5 – Измерение положения посадочных мест под чувствительные элементы: 1 - лазер и теодолит; 2 – большое зеркало; 3 – контролируемая площадка; 4 – «базовая» площадка (α = 10˚02’34’’)

 

Оптические оси базовой и исследуе­мой площадок лежат в одной плоскости. Если они параллельны друг другу, то за­дается условие перекрестия. Расстояние и углы между зеркалами 3 и 4 в процессе проведения измерений не изменяют свою величину. На рис. 5 приводится опытная схема измерений угла между зеркалами 3 и 4 с использованием оптического усили­теля (зеркало 2). После каждого вида ис­пытаний узел посадочной площадки ин­дивидуально устанавливается в схему вертикального контроля. При проведении испытаний требуется минимизировать деформацию поверхности зеркал от торцевых нагрузок в пределах 10''. В соответствии с комплексной программой экспериментальной отра­ботки собранный узел посадочного места зеркала подвергается испытаниям с целью подтверждения сохранности его характе­ристик: транспортные технологические испытания; испытания на прочность к воздействию линейных ускорений по осям Х и Y (вдоль оптической оси зеркала и в поперечном направлении); испытания на кратковременные динамические ускоре­ния по осям Х и Y; испытания на проч­ность к воздействию пониженной (- 50°С) и повышенной (+ 50°С) температуры; термовакуумные испытания, при которых температура зеркала изменялась в преде­лах ±5°С; при этом во всем диапазоне из­менения температуры от +12°С до +28°С контролируется качество зеркала.

При выборе параметров лазерного излучения, расчёт которых следует про­вести, необходимо исходить из того, что их число должно быть минимальным, так как большой объём полученных результа­тов может затруднять их использование. Как правило, наибольшие изменения аберраций имеют место для лучей, иду­щих на край входного зрачка и край поля изображения. Поэтому для подавляющего большинства оптических систем доста­точно ограничиться расчётом следующих лучей: для точки на оси – луча, идущего на край входного зрачка и для края поля изображения – главного луча; двух мери­диональных лучей, идущих на верхний и нижний края входного зрачка (с учётом виньетирования) и одного внемеридио­нального луча, идущего в точку зрачка с координатами m=0, M=m_max, где m_max – ра­диус зрачка.

Для оптических систем, работающих с большой числовой апертурой (с боль­шим относительным отверстием), целесо­образно рассчитать осевой и внеосевой лучи для зоны входного зрачка с коорди­натой m =. Для систем со сред­ними и большими полями изображений следует дополнительно рассчитать лучи пучка, идущего из точки предмета с орди­натой y = (или при  для  =), где y_max – размер предмета, _max – синус угла поля.

Основными требованиями на первом этапе контроля посадочных мест под чув­стви­тельные элементы являются: диапа­зон измерений -  от 0' до 10'. погрешность из­мерения - 10'', измерения проводятся при нормальных условиях. Параметры ок­ружающей среды не оказывают влияния на точность измерений при обеспечении их стабильности в следующих диапазо­нах: по температуре - ±5°С; по влажности - ±5%; по давлению - ±10 мм рт. ст., - до­пустимая амплитуд  виброперемещений – не более 5 мм на дистанции 20 м. Система измерений должна позволять производить измерения перемещений по трем координатам, при этом взаимное расположе­ние измеряемых элементов может быть произвольным без ограничения на степень свободы.

Экспериментальные исследования проводились согласно схеме на рис. 4. При отработке методики использовался теодолит 2Т2А, излучатель – полупровод­никовый лазер IDL5S-640. Точность из­мерений составляла 3’’. При длине базо­вой оси 3 м влияние внешних воздействий не наблюдается.

В результате проведённого анализа выявлены следующие первичные погреш­ности, определяющие точность измерения линейных и угловых координат контроли­руемого объекта: погрешность измерения координат центра изображения измери­тельной марки на ПЗС-матрице измери­тельного оптико-электронного преобразо­вателя, обусловленная шумами и дискрет­ностью приёмной площадки и погреш­ность измерения, определяемая отклоне­нием величины фокусного расстояния объективов от номинального значения.

Таким образом, разработанная мето­дика контроля положений посадочных мест с использованием полупроводнико­вого лазера позволяет сократить трудоём­кость испытаний, в том числе процесса наладки системы, в 3–4 раза. При этом точность измерений системы составляла 0,1'', а при длине базовой оси 3 м влияние внешних воздействий не наблюдается.

Литература

1. Ворона А.М., Коняхин И.А. Исследование регулярного виньетирования в оптико-электронных системах измерения угловых деформаций крупногабаритных конструкций // Изв. ВУЗов. «Приборостроение». Т. 51, 2008. № 9. С. 14-18.
2. Аникст Д.А., Константинович К.М., Меськин И.В. Высокоточные угловые из­мерения. М.: Машиностроение, 1987. 480 с.
3. Михеев С.В., Коняхин И.А. Моделирование оптической системы измерения координат объекта методом обратной линейной засечки // Сборник трудов VI Международной конференции “Прикладная оптика” 18-21 октября 2004 г, СПб, Т.1 "Оптическое приборостроение". СПб.: 2004. С. 335-338.
4. Коняхин И.А. Панков Э.Д. Трёхкоординатные оптические и оптико-электронные угломеры. М.: Недра 1991. 224 с.
5. Михеев С.В. Моделирование оптической системы измерения координат объекта методом обратной угловой за­сечки //Сборник трудов II межвузовской конференции молодых учёных 28–31 марта 2005 г./ Под редакцией В.Л. Ткалич. Том 3. СПб: СПбГУ ИТМО, 2005. С. 180-183.

References

1. Vorona A.M., Konjahin I.A. Issledovanie reguljarnogo vin'etirovanija v optiko-jelektronnyh sistemah izmerenija uglovyh deformacij krupnogabaritnyh konstrukcij // Izv. VUZov. «Priborostroenie». T. 51, 2008. № 9. S. 14-18.
2. Anikst D.A., Konstantinovich K.M., Mes'kin I.V. Vysokotochnye uglovye izmerenija. M.: Mashinostroenie, 1987. 480 s.
3. Miheev S.V., Konjahin I.A. Modelirovanie opticheskoj sistemy izmerenija koordinat ob#ekta metodom obratnoj linejnoj zasechki // Sbornik trudov VI Mezhdunarodnoj konferencii “Prikladnaja optika” 18-21 oktjabrja 2004 g, SPb, T.1 "Opticheskoe priborostroenie". SPb.: 2004. S. 335-338.
4. Konjahin I.A. Pankov Je.D. Trjohkoordinatnye opticheskie i optiko-jelektronnye uglomery. M.: Nedra 1991. 224 s.
5. Miheev S.V. Modelirovanie opticheskoj sistemy izmerenija koordinat ob#ekta metodom obratnoj uglovoj zasechki //Sbornik trudov II mezhvuzovskoj konferencii molodyh uchjonyh 28–31 marta 2005 g./ Pod redakciej V.L. Tkalich. Tom 3. SPb: SPbGU ITMO, 2005. S. 180-183.