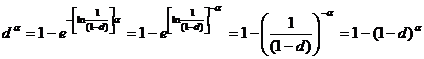USING OF THE DIFFICULTY OF ACHIEVING THE GOAL FOR EVALUATION OF SYNERGETIC EFFECT IN THE CREATION OF INTEGRATED STRUCTURES

Алексеев А.П.¹, Абрамов Г.В.², Булгакова И.Н.³

¹Аспирант, ²доктор технических наук, профессор, ³кандидат экономических наук, Воронежский Государственный Университет

ИСПОЛЬЗОВАНИЕ ТРУДНОСТИ ДОСТИЖЕНИЯ ЦЕЛИ ДЛЯ ОЦЕНКИ СИНЕРГЕТИЧЕСКОГО ЭФФЕКТА ПРИ СОЗДАНИИ ИНТЕГРИРОВАННЫХ СТРУКТУР

Аннотация

Получение синергетических эффектов от совместной деятельности – важное конкурентно преимущество. В статье проанализированы существующие подходы к оценке синергизма, они сильно ограничены и не могут быть использованы для интегральной оценки. Построена оптимизационная модель оценки синергетического эффекта на основе универсальных гибких параметров -  трудностей достижения цели.

Ключевые слова: интеграция предприятий, синергетический эффект, трудность достижения цели.

Alekseev A.P.¹, Abramov G.V.², Bulgakova I.N.³

¹Postgraduate student, ²PhD in Engineering, professor, ³PhD in Economics, Voronezh State University

USING OF THE DIFFICULTY OF ACHIEVING THE GOAL FOR EVALUATION OF SYNERGETIC EFFECT IN THE CREATION OF INTEGRATED STRUCTURES

Abstract

Receiving of synergic effects by cooperative activities is important competitive advantage. This article analyzes exist approaches to synergy valuation, they are limited and cannot be used for integral valuation. We suppose the optimization model for valuation of synergic effects based on flexible universal parameters - difficulties of achieving the goal.

Keywords: enterprises integration, synergic effect, difficult of achieving the goal.

Основная цель взаимодействия предприятий на основе интеграции экономических процессов – получение синергетических преимуществ от совместной деятельности. Ведь создание и функционирование интегрированных структур целесообразно только тогда, когда оно приносит положительный, стабильный эффект [1].

Создателем синергетического направления в науке является Герман Хакен [2]. Синергетика занимается изучением систем, состоящих из большого числа частей, компонентов или подсистем, сложным образом взаимодействующих между собой. При этом возможно появление синергетического эффекта. Синергетический эффект в экономике означает превышение совокупных результатов деятельности интегрированной экономической системы от суммы результатов деятельности предприятий до их объединения в интегрированную экономическую систему.

Различают два вида синергии: синергию, возникающую за счет субаддитивности, и синергию, возникающую за счет супераддитивности. Синергический эффект неосязаем и настолько неуловим, что предсказать или определить его отдельному человеку практически невозможно. Именно поэтому анализ и оценку величины синергического эффекта рекомендуется осуществлять многочисленным коллективом [3].

Среди показателей синергизма можно выделить [4]:

– ускорение темпов роста объемов производства и (или) продаж на фоне развертывания совместной деятельности;

– достижение экономии накладных расходов и транзакционных [5] издержек в рамках интегрированного предприятия;

– улучшение соотношения «цена – качество» по номенклатурным группам товаров, производимых совместно;

– наращивание доли продаж в разрезе продуктовых групп объединения;

– увеличение инвестиционного потока в программы совместной деятельности предприятий и т.д.

Критерии и показатели эффекта интеграции процессного типа в последние годы активно разрабатывались Ю.В. Якутиным [6], например, коэффициент собственных НИОКР, коэффициент внутренней кооперации, коэффициент внутреннего кредитования и т.д.

К сожалению, использование в системах корпоративного менеджмента качественно и количественно определенных показателей синергетического эффекта совместной деятельности бизнес-единиц на практике пока является экзотикой [7]. Применение традиционных способов детерминированного  анализа для расчета эффекта синергии («неразложимого остатка») в случаях одновременного изменения значений факторов мультипликативных моделей сопряжено с некоторыми недочетами и неточностями [8]. В частности:

- использование интегрального метода предполагает равномерное распределение результата синергии («неразложимого остатка») между всеми факторами, повлиявшими на его формирование, независимо от уровня их изменения;

- логарифмический метод учитывает изменение фактора относительно его первоначального уровня (использование индексов), а не степень участия (его значение относительно изменения других факторов) в образовании «дополнительного» результата;

- Метод цепных подстановок и метод абсолютных разниц характеризуются наиболее существенными недостатками, поскольку основаны на определенной последовательности изменений факторов модели, в которой в первую очередь изменяются количественные, а затем качественные факторы, что, в свою очередь, влияет на степень их воздействия на конечный  результат изменения. [8].

Помимо традиционных методов также были разработаны более углубленные методы расчета синергетического эффекта в узких областях, таких как торговый, инвестиционный и управленческий синергизм, которые, однако, неприменимы в других областях оценки синергии. Кроме отсутствия универсальности, эти методы также ограничены во взаимодействии друг с другом ввиду использования принципиально разных подходов.

Для расчета синергизма современных предприятий необходима универсальная и гибкая методика, не привязанная к конкретным показателям работы предприятия, а использующая вместо фактических данных оценки определенной структуры. Вариантом подхода к гибкому формализованному представлению процесса принятия решения описывает теория полезности, одним из воплощений которой является модель Р. Стоуна [9].

Будем понимать под термином «полезность» количественную оценку предпочтения одного набора параметров организации другому. Под параметрами организации нами понимаются показатели, характеризующие предприятие с точки зрения различных областей деятельности.

Рассмотрим набор из n параметров - вектор , координата  которого показывает количественную оценку некоторой характеристики работы предприятия. Выбор организации характеризуется отношением предпочтения - на множестве  наборов  определена функция полезности , значение которой при наборе  равно оценке полезности, которую предприятие дает этому набору. Ее можно называть степенью удовлетворения потребностей организации, если она достигает данного значения параметров.

Для модели Стоуна функция полезности имеет вид [10]:

                                                                     (1)

Если при этом существует  бюджетное ограничение, то

                                                                                                     (2)

Здесь  – минимально необходимый уровень i-го параметра, который должен быть достигнут в любом случае. Для того чтобы набор  мог быть полностью приобретен, необходимо, чтобы доход I превышал стоимость набора. Цена  – оценка стоимости повышения i-го параметра на одну единицу, I – доход организации. Показатели степени  характеризуют относительную ценность благ для предприятия.

Задача рационального поведения предприятия заключается в выборе такого набора, который максимизирует функцию полезности при заданном бюджетном ограничении. Очевидно, что оптимальный набор обращает бюджетное ограничение в равенство, тогда задачу выбора можно заменить задачей на условный экстремум, для решения которой применим метод Лагранжа [10].

Универсальность модели Стоуна позволяет использовать ее для сравнения полезностей наборов различных параметров [9].

Однако также необходим гибкий механизм приведения различных по своей природе параметров к единообразной оценке полезности. В качестве меры полезности, по нашему мнению, могут выступать оценки типа «трудности достижения цели» [11], которые являются, с одной стороны, мерой несоответствия фактического качества ресурсов системы и требований к этому качеству, с другой - обобщенной оценкой качества.

Понятие «трудность» исходит из соображений о том, что получить результат определенного качества тем труднее, чем ниже качество ресурсов, подаваемых на входе, и выше требования к качеству результат на выходе, при прочих равных условиях [12].

Пусть есть некая система, на входе которой подается набор ресурсов i, необходимых для достижения результата. Величиной  обозначим оценку качества ресурса i, заданную в полуинтервале . Так как не все значения качества ресурсов достижимы, имеет смысл ввести минимальное требование к качеству ресурса , так же заданное в полуинтервале . Невыполнение минимального требования к качеству автоматически ведет к невыполнению требований качества результата, поэтому .

Чтобы определить трудность  как функцию оценки качества ресурса и требования к качеству, нужно обозначить свойства этой функции:

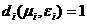1. , при 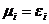, т.е. трудность достигает максимального значения в том случае, когда качество ресурса находится на минимальном уровне и равно требованию к качеству.
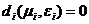2. , при 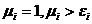, т.е. трудность минимальна в том случае, когда качество ресурса достигает своего максимального значения, если требования к качеству ниже этого значения.
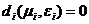3. , при 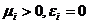, т.е. трудность минимальна при любом качестве ресурса, если требований к качеству нет.

Этим трем свойствам отвечает функция [13]:

 , при этом                             (3)

Так как качество результата можно трактовать как иерархическую совокупность его отдельных свойств [14], то оценка качества результата, выражаемая через частные трудности , должна быть интегральной и является функцией оценок отдельных свойств.

Если результат зависит от двух ресурсов или может быть охарактеризован двумя свойствами, оценки трудности которых имеют значения  и , то интегральная оценка будет иметь вид .

Данная оценка должна удовлетворять следующим требованиям:

1. Ассоциативность - .
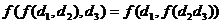2. Коммутативность - .
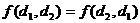3. Ограниченность - .
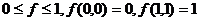4. Нейтральность нулевого значения компонент - .

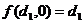Как показано в [13] всем перечисленным условиям удовлетворяет функция:

                                                    (4)

Эту операцию обозначим как обобщенное сложение трудностей [14]:

Тогда операция обобщенного умножения на некоторое число , согласованная с операцией обобщенного сложения, может быть задана в форме:

 .                                                                                   (5)

Операция обобщенного возведения в степень будет иметь вид:

                                                                                        (6)

Знак соответствует операции обобщенного возведения в степень .

Формула (3) легко может быть обобщена на случай n компонент:

                                                                                        (7)

Полученные оценки являются оценками того же типа, что и d, т.е. оценками трудности достижения цели [8], которые могут использоваться как гибкие и универсальные параметры для различных моделей, в том числе модели Стоуна.

Воспользуемся оценками трудности достижения нужных уровней параметров как мерой их полезности в формуле (1). Представим общую полезность набора параметров/ресурсов как интегральную оценку трудности достижения этого набора с учетом относительных ценностей:

                                                                              (8)

где  - вектор оценок трудностей достижения цели.

Функция (8) является аддитивной относительно параметров трудности,  каждый из которых взвешивается коэффициентом , характер которого указывает на относительную ценностью параметра для предприятия. Операция   суммирования в (8) представляет собой операцию обобщенного сложения трудностей по аналогии с (7),  - коэффициент в операции обобщенного возведения в степень по аналогии с (6).

Объединим операции обобщенного сложения и возведения в степень.  На примере двух параметров, используя (4), данное объединение будет иметь вид:

                      (9)

Упростим операцию возведения трудности в степень, используя (6):

            (10)

Тогда формула (8) с учетом этих преобразований принимает вид:

                     (11)

Рассмотрим пример системы из двух параметров, которые обладают оценками качества  и , и требованиями к качеству  и  соответственно.

На данном этапе положим относительные ценности параметров максимальными, т.е. .

Пусть параметры обладают следующими характеристиками:

Рассчитаем трудности по формуле (3):

Отметим, что, несмотря на почти одинаковую оценку качества, трудность достижения цели для этих двух параметров разительно отличается ввиду разных требований к качеству.

Вычислим интегральную оценку трудности по формулам (4) и (7):

Несмотря на очень низкую трудность для первого параметра, интегральная оценка получилась относительно высокой, т.к. относительная ценность обоих параметров одинакова.

Сравним результат с трудностью достижения этих же параметров при условии высокой ценности первого и низкой ценности второго.

Пусть , .

Воспользуемся формулой (11):

Отметим, что высокая ценность параметра с низкой трудностью почти никак не повлияла на итоговую оценку, в то время как снижение ценности параметра с высокой трудностью серьезно ее сократило.

Теперь положим , , тогда:

Можно сделать вывод, что ценность параметра с низкой трудностью не критична для итоговой интегральной оценки, для снижения общей трудности гораздо существеннее ценность параметров с высокими трудностями.

Полученные таким методом оценки полезности показателей не зависят от количественных и качественных характеристик этих показателей и могут использоваться как гибкие и универсальные параметры, как для схематичных моделей, так и для вполне конкретных характеристик функционирования предприятий.

Литература

1. Сибирская Е.В. Комплексный подход к инновационному развитию Орловского региона / Е.В. Сибирская, Д.Г. Булгаков // Инновационный вестник Регион. – 2007. – № 1 (7). – С. 8–14.
2. Климонтович Н.Ю. Без формул о синергетике. Минск: Вышэйшая школа, 1986. 458 c.
3. Жемчужников С.И. Направления совершенствования взаимодействия предприятий на основе интеграции экономических процессов // Инновационные Технологии Управления. ИнВестРегион. 2011. № 1. - С. 20-26.
4. Козенкова Т.А. О построении системы показателей синергетического эффекта финансово-экономической интеграции. Изд. дом «Экономическая газета», Бухгалтерский учет и анализ, 2011. – С.61-68.
5. Coase R.H. The nature of the firm // Economica.1937. V. 4. P. 15.
6. Якутин Ю.В. Модели корпоративной интеграции: проектирование, развитие, эффективность. М.: Изд. дом «Экономическая газета», 2006. - С. 238.
7. Масютин С.А. Корпоративное управление: опыт и проблемы М.: Финстатинформ, 2003. 280 с.
8. Алексеев А.П. Совершенствование методики оценки синергетического эффекта процесса интеграции предприятий // Евразийский союз ученых. 2014. №9. – С. 14-17.
9. Алексеев А.П. Использование модели Р. Стоуна для оценки синергетического эффекта процесса интеграции предприятий // Наука и образование в жизни современного общества. 2014. №11. С. 10-11.
10. Бабушкин Ю.В., Новикова А.Г. Разработка программно-алгоритмического обеспечения рабочего места математика-экономиста. Молодежь и современные информационные технологии. Труды конференции. Томск, изд. ТПУ, 2004 г.
11. Руссман И.Б., Леденева Т.М. Некоторые способы построения интегральных оценок для агрегирования ресурсов // Оптимизация и моделирование в автоматизированных системах: Межвузовский сборник научных трудов. 1991. - С.122–124.
12. Булгакова И.Н., Саликов Ю.А. Совершенствование модели развития социально-экономических систем // Современная экономика: проблемы и решения – Воронеж, 2010 - №2(2) – С. 146-154.
13. Руссман И.Б. Интегральные оценки качества в организационных системах // Сборник "Структурная адаптация сложных систем управления", Изд. ВПИ, Воронеж, 1977, с. 90-92.
14. Бермант М.А., Руссман И.Б. О проблеме оценки качества // Экономика и математические методы. 1978. №4.

References

1. Sibirskaja E.V. Kompleksnyj podhod k innovacionnomu razvitiju Orlovskogo regiona / E.V. Sibirskaja, D.G. Bulgakov// Innovacionnyj vestnik Region. – 2007. – № 1 (7). – S. 8–14.
2. Klimontovich N.Ju. Bez formul o sinergetike. Minsk: Vyshjejshaja shkola, 1986. 458 c.
3. Zhemchuzhnikov S.I. Napravlenija sovershenstvovanija vzaimodejstvija predprijatij na osnove integracii jekonomicheskih processov // Innovacionnye Tehnologii Upravlenija. InVestRegion. 2011. № 1. - S. 20-26.
4. Kozenkova T.A. O postroenii sistemy pokazatelej sinergeticheskogo jeffekta finansovo-jekonomicheskoj integracii. Izd. dom «Jekonomicheskaja gazeta», Buhgalterskij uchet i analiz, 2011. – S.61-68.
5. Coase R.H. The nature of the firm // Economica.1937. V. 4. P. 15.
6. Jakutin Ju.V. Modeli korporativnoj integracii: proektirovanie, razvitie, jeffektivnost'. M.: Izd. dom «Jekonomicheskaja gazeta», 2006. - S. 238.
7. 7. Masjutin S.A. Korporativnoe upravlenie: opyt i problemy M.: Finstatinform, 2003. 280 s.
8. Alekseev A.P. Sovershenstvovanie metodiki ocenki sinergeticheskogo jeffekta processa integracii predprijatij // Evrazijskij sojuz uchenyh. 2014. №9. – S. 14-17.
9. Alekseev A.P. Ispol'zovanie modeli R. Stouna dlja ocenki sinergeticheskogo jeffekta processa integracii predprijatij // Nauka i obrazovanie v zhizni sovremennogo obshhestva. 2014. №11. S. 10-11.
10. Babushkin Ju.V., Novikova A.G. Razrabotka programmno-algoritmicheskogo obespechenija rabochego mesta matematika-jekonomista. Molodezh' i sovremennye informacionnye tehnologii. Trudy konferencii. Tomsk, izd. TPU, 2004 g.
11. 11. Russman I.B., Ledeneva T.M. Nekotorye sposoby postroenija integral'nyh ocenok dlja agregirovanija resursov // Optimizacija i modelirovanie v avtomatizirovannyh sistemah: Mezhvuzovskij sbornik nauchnyh trudov. 1991. - S.122–124.
12. Bulgakova I.N., Salikov Ju.A. Sovershenstvovanie modeli razvitija social'no-jekonomicheskih sistem // Sovremennaja jekonomika: problemy i reshenija – Voronezh, 2010 - №2(2) – S. 146-154.
13. Russman I.B. Integral'nye ocenki kachestva v organizacionnyh sistemah // Sbornik "Strukturnaja adaptacija slozhnyh sistem upravlenija", Izd. VPI, Voronezh, 1977, s. 90-92.
14. 14. Bermant M.A., Russman I.B. O probleme ocenki kachestva // Jekonomika i matematicheskie metody. №4.