Modelling of warehouses for the storage of railway track top construction materials
Modelling of warehouses for the storage of railway track top construction materials
Abstract
Ensuring uninterrupted operation of the country's railway transport infrastructure is the most important task to be solved in the interests of both stable operation of industrial enterprises and ensuring safety. Within the framework of engineering and organizational measures aimed at solving this task, the timely creation of stocks of material resources required for construction and restoration work on railways is important.
The use of modern modelling methods at the stage of concept development for the creation of storage bases for construction and restoration materials should help in the analytical evaluation of available options for the implementation of the developed solutions, including for the purpose of objective assessment of the degree of load on their individual elements and the formation of proposals for ways of functioning and composition.
The article describes the method of application of modelling methods developed by the author to estimate the effect obtained by changing the areas of storage sites and different strategies for managing the flow of incoming and outgoing materials. The assessment is made on the basis of the expected production volumes of construction and rehabilitation works and the capacity of the enterprises to supply railway track superstructure materials. The result of modelling is probabilistic parameters of states of storage bases of material supplies.
The main purpose of the models development is the scientific substantiation of the preliminary assessment of the options for the creation of warehouses for the storage of railway track superstructure elements, under the conditions of the initial data deficit and the complexity of the field experiment with real objects, by solving the problem of calculating the main parameters of the storage areas. The tasks solved in the process of research include: analysis of the degree of loading of warehouses and mathematical justification of their optimal capacity in order to reduce the idle time of storage areas and ensure the continuity of production processes at work sites.
The studied processes were modelled on the basis of the adopted variants of organization and technology of work execution. The developed models can be used both to solve current planning tasks and to act as a source of statistical data for organizationally connected multichannel models of transport construction formations functioning in the process of construction and restoration works.
1. Введение
В Российской Федерации железнодорожная сеть всегда являлась одним из важнейших элементов инфраструктуры государства, обеспечивающей транспортную связь регионов и городов, являющуюся одним из локомотивов роста экономического потенциала и обороноспособности страны .
Инфраструктура железнодорожного транспорта общего пользования – технологический комплекс, включающий в себя железнодорожные пути общего пользования и другие сооружения, железнодорожные станции, устройства электроснабжения, сети связи, системы сигнализации, централизации и блокировки, информационные комплексы и систему управления движением и иные обеспечивающие функционирование этого комплекса здания, строения, сооружения, устройства и оборудование .
В свое время термин «инфраструктура» пришел из военного дела, в котором под ним понимается система из сооружений, предназначенная для обеспечения действий войск (сил) в которую входят склады вооружения, боеприпасов и материальных средств, полигоны, аэродромы и прочее .
И в настоящее время от инфраструктуры железнодорожного транспорта на прямую зависит не только состояние экономики страны, но и ее безопасность. К решению задач по обеспечению бесперебойности её функционирования привлекаются специальные формирования Федеральных органов исполнительной власти и подразделения силовых ведомств.
При решении этих задач выполняются мероприятия по осуществлению всесторонней подготовки объектов транспортной инфраструктуры, привлекаемых сил и средств, к восстановлению поврежденных, сооружению новых и ремонту существующих объектов инфраструктуры железнодорожного транспорта.
Выполнение данных мероприятий требует использования запасов различного рода материальных средств, к первоочередным из которых можно отнести элементы верхнего строения железнодорожного пути. Общие вопросы организации хранения верхнего строения железнодорожного пути отражены в разделе V Правил «Требования к хранению, транспортированию и складированию материалов верхнего строения железнодорожного пути для обеспечения охраны труда работников». Но в настоящее время не до конца проработан вопрос по расчету потребных объемов находящихся на складах материалов и мест их расположения. В настоящее время объемы хранения определяются исходя из установленных в норм покилометрового запаса материалов верхнего строения пути для главных путей железных дорог и порядка их применения, порядок организации хранения определен в . Но данные нормы не в полной мере учитывают случаи производства значительных объемов работ, по укладки верхнего строения железнодорожного пути, выполняемых в соответствии с текущей обстановкой, которая может сложиться при стихийных бедствиях, в ходе подготовки и ведения боевых действий. В этих случаях для обеспечения установленных темпов сооружения верхнего строения железнодорожного пути склады (в том числе вновь сформированные) должны иметь оптимальное расположение и емкость площадок хранения. В настоящей статье описываются модели, которые можно использовать для решения данной задачи. Модели относятся к вероятностным математическим и базируются на теории управления запасами с использованием аппарата теории массового обслуживания на основе Марковских случайных процессов.
Эффективное использование складских площадей в этом случае будет выступать в качестве основного целевого показателя эффективности функционирования системы .
2. Описание математической модели
Возможности обеспечения требуемого темпа сооружения верхнего строения железнодорожного пути (далее – ВСЖП) возможно только в случае бесперебойного подвоза его элементов к месту производства работ. В свою очередь, решение этой задачи обеспечивается только при поддержании требуемого значения вероятности наличия запаса материальных средств на складах с которых организована их поставка. Соответственно, при наличии непосредственной связи между поддержанием требуемых темпов выполнения работ по укладке пути и доступными запасами материальных средств, постановку задачи можно изложить как определение рациональных объемов хранения запасов ВСЖП с учетом принятой стратегии управления и директивных ограничениях.
Наиболее очевидным будет использование вероятностной модели построенной с использованием аппарата теории массового обслуживания, представляя имеющиеся складские запасы материальных средств в виде очередей, при этом параметрами определяющими интенсивности восполнения и расходования материальных средств будут выступать потоки поступления заявок (λ) и их обслуживания (μ). Данный аппарат теории массового обслуживания работает с дискретными величинами, что полностью соответствует моделируемым процессам. Для упрощения расчетов в модели в качестве расчётной единицы берется количество материалов, содержащихся на складе, потребное для сооружения одного метра ВСЖП.
В случаях когда склад хранения запасов ВСЖП организуется в целях текущего обеспечения строительно-восстановительных работ, в таком случае, как правило, объемы единовременной поставки материальных средств на порядок больше, чем разовые объемы отгрузки. В частности, поставка может осуществляются с использованием подвижного железнодорожного состава, а отгрузка, для укладки портальными тракторными путеукладчиками, на путевые тележки. При этом за расчётную единицу должен приниматься средний объем отгружаемой партии ВСЖП, в единицах которой необходимо измерять объемы поступающих материальных средств. В отдельных случаях может наблюдаться картина когда интенсивность поступления материальных средств на склад совпадает с интенсивностью отгрузки (выдачи), что может определяться удаленностью от производственных площадок или центральных баз хранения. Для площадок организуемых в местах сборки звеньев рельсошпальной решетки будет характерна картина когда поступление материалов (готовых звеньев РШР) будет происходить более мелкими партиями, чем отгрузка.
Временно организуемые площадки (склады) хранения материалов ВСЖП, создаваемые в районах по возможности приближенных к местам производства работ, будут характеризоваться тем, что отгрузка материальных средств будет осуществляться фактически непрерывно, при этом потоки поступления и отгрузки материалов должных быть примерно равными. В том случае постановка задачи на моделирование может быть сформулирована следующим образом «Определение вместимости склада, в целях обеспечения наименьшей вероятности полного расходования хранящихся материальных средств», данную постановку можно дополнить еще одним условием «Определение вместимости площадок хранения склада, обеспечивающих наименьшую вероятность отсутствия свободных площадей, в любой момент времени». С помощью методов теории массового обслуживания данная задача может решаться с применением многоканальных систем массового обслуживания , в этом случае вместимость площадок хранения определяется числом каналов, выражающимся через равные объемы поставок и выдачи ВСЖП.
При текущей постановки задачи возможно ввести следующие допущения:
- максимальное число партий поставки на склад равно N,
- при выдаче очередной партии ВСЖП незамедлительно формируется заявка на поставку очередной партии для покрытия текущего некомплекта,
- отгрузка материальных средств со склада осуществляется с интенсивностью λ,
- в случае пустого склада, отгрузка не выполняется,
- усредненная продолжительность выполнения заявки на поставку равна Т = 1 / μ.
Соответственно, получилось описание системы в которой обеспечено непрерывное пополнение запасов ВСЖП, и суммарное значение имеющихся и заказанных материальных средств в поставляемых и отгружаемых партиях будет равно фиксированному числу N.
Данная модель, аналогична описанной в и относится к системе массового обслуживания, в качестве требований при этом выступают отгрузки материалов, а обслуживанием будет представляться поставка на склад новых партий.
Вероятности состояний системы можно представить в виде дифференциальных уравнений
В стационарном режиме, решение будет иметь следующий вид:
Для вероятности пустого склада
Вероятность наличия на складе n партий материальных средств
Вероятность заполнения всего объема склада (прием новых партий невозможен)
Определение средних значений запаса на сладе (в партиях поставки) можно вычислить выражением
Описанную модель можно использовать для определения параметров временных «полевых» площадок хранения материалов, для вариантов когда поставка осуществляется подвижным составом с интенсивностью μ, а выдача выполняется для покрытия, поступающих случайным образом от восстановительных подразделений, заявок с интенсивностью λ. Вычисление количественных показателей ВСЖП, исходя из расчётных партий поставок выполняется перемножением количества партий поставки – n на их единичный размер – q.
В этом случае требуемый размер складских площадок может быть вычислен исходя из их вместимости и заданных вероятностей опустошения склада, объема партии поставки и усредненных значений запасов материальных средств обеспечиваемых в заданном периоде.
Самым частым случаем будет ситуация, в которой размер поставляемой партии материалов значительно больше, чем объем партии отгрузки. Данный вариант реализуется при организации хранения материалов на складах путевых машинных станций АО «РЖД» и хранилищах Росрезерва, при их вывозе непосредственно на объекты производства работ. В таком случае будет актуальна задача определения оптимальных (рациональных) площадей площадок хранения и размеров принимаемых партий материальных средств, нацеленная на общее снижение затрат на содержание и обслуживание складских территорий.
Рассмотрим вариант расчета для следующих исходных данных.
Выполняется строительство (восстановление) участка железнодорожного пути, при котором требуется производство работ по укладки 1000 м рельсошпальной решетки (далее – РШР). Расстояние от базы хранения до места производства работ 5000 м. Отгрузка выполняется на путевые тележки типа ПТ-13 пакетами по три звена длинной по 25 метров, всего в партии 150 м. Скорость транспортировки к месту производства работ автомобильным транспортом, оборудованным универсальным устройством комбинированного хода, обеспечивающим возможность его движения по железнодорожному пути, составляет 1,389 м/с (5 км/ч).
Погрузка (выгрузка) пакета звеньев РШР (в одном пакете 3 звена РШР по 25 м) с железнодорожных платформ на складские площадки (со складских площадок на путевые тележки) занимает – 960 с (16 минут), 1 920 с для партии при использовании одного автомобильного крана . Временные затраты на разгрузку и укладку одного звена РШР составляет – 510 с (8,5 мин), для пакета – 1530 с (25,5 мин), 3 060 для партии. Общее время между отгрузками партий со склада 9 960 с.
Поставка партии РШР на склад выполняется со склада Росрезерва находящегося на удалении – 500 000 м с использование подвижного железнодорожного состава, партиями объемом по – 2 пакетов РШР на четырёхсотой платформе, в расчетном поезде 30 платформ, общий объем партии – 4 500 м (30 партий отгрузки), скорость движения поезда - 19,444 м/с (70 км/ч), время выгрузки 57 600 с (960 мин), среднее время выполнения одной поставки 83 314 с (2 777 с/партию отгрузки). Исходные данные для расчетов приведены в таблице 1.
Таблица 1 - Основные параметры склада
№ п/п | Параметр | Условное обозначение | Значение |
1 | Размер пакета отгрузки материалов ВСП (погонных метров) | q | 150 |
2 | Интенсивность отгрузки партий материалов со склада (шт./с) | λ | 0,00036 |
3 | Интенсивность поступления партий материалов на склад (шт./с) | μ | 0,0001 |
4 | Максимально возможное число парий поставки на склад (шт.) | N | 4 |
5 | Время поставки партии на склад (с) | Т | 83 314 |
7 | Размер партии поставки ВСП на склад (партия отгрузки) | w | 30 |
Исходя из приведенных исходных данных, выполнив расчёты для стационарного режима, мы получаем следующие значения.
Согласно (2) вероятность пустого склада Р0 = 0,28.
Согласно (3) вероятность наличия на складе n партий материальных средств при выполнении условия n<N
Р1 = 0,52
Р2 = 0,30
Р3 = 0,14
По формуле (4) рассчитываем вероятность заполнения всего объема склада Р4 = 0,04.
Также по выражению (5) вычислим средние значения запаса на сладе (в партиях поставки)
Zсред. = 1,725
Полученные при расчётах результаты показывают, что емкость склада рассчитанная на 4 партии с высокой вероятностью позволит обеспечить снабжение восстановительных работ потребными материалами.
Но что будет, если мы увеличим темп производства работ за счет сокращения времени укладки на 15 минут, в том случае интенсивность отгрузки партий материалов со склада (шт./с) λ = 0,00053.
Выполним расчёт мы получаем следующие значения.
Согласно (2) вероятность пустого склада Р0 = 0,42.
Согласно (3) вероятность наличия на складе n партий материальных средств при выполнении условия n<N
Р1 = 0,43
Р2 = 0,19
Р3 = 0,06
По формуле (4) рассчитываем вероятность заполнения всего объема склада Р4 = 0,01.
Также по выражению (5) вычислим средние значения запаса на сладе (в партиях поставки) Zсред. = 1,07.
Расчеты показывают, что в данном случае складские площади рассчитанные на хранение 4 партий РШР будут избыточными.
При таком подходе управление объемами хранимых материальных средств производится через заявки на поставку и отгрузку. Рациональные площади хранения определяются для установившихся режимов работы складских площадок, задающихся значениями вероятностей пустого склада и (или) пустующих площадей, а также уровнем среднего объемах находящихся на хранении материалов.
Определение усредненного объема отгружаемых партий – q, а также интенсивности поступления заявок на отгрузку – μ производится по выражению
где Gмес. – среднесуточный (среднемесячный, среднегодовой, среднеквартальный) объём отгрузки материальных средств со склада, в метрах ВСЖП.
Представим объем партии поставки материальных средств на склад, для хранения – Q в партиях отгрузки для производства строительно-восстановительных работ на объектах – q, что позволит использовать аппарат теории массового обслуживания. При этом примем отношение .
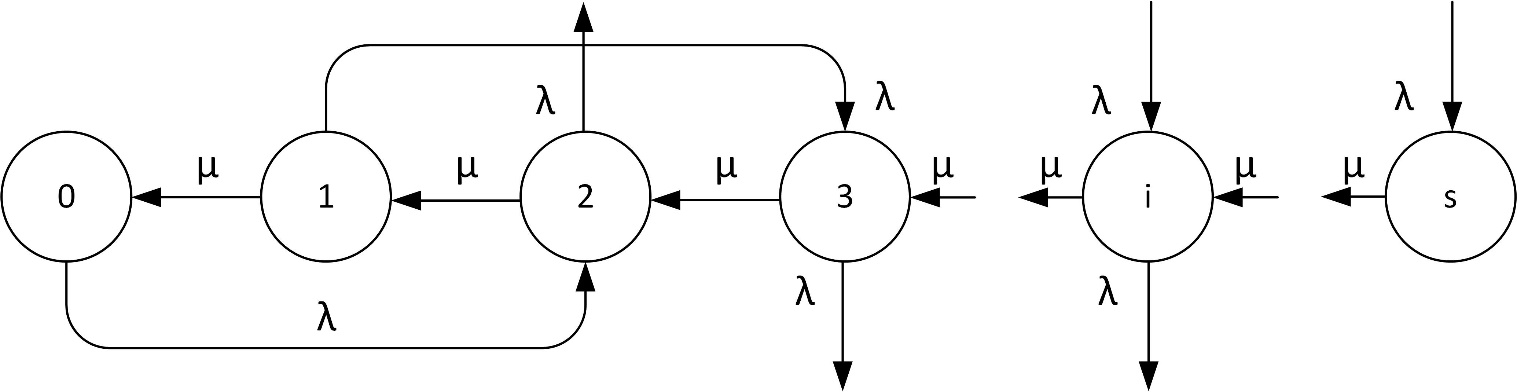
Рисунок 1 - Граф вероятностей состояний складских запасав материальных средств
Состояния системы массового обслуживания, схематично изображенной на рисунке 1, имеют следующий характер:
0 – на складских площадках отсутствуют запасы материальных средств;
1 – запас материальных средств на складских площадках позволяет осуществить одну отгрузку;
2 – запасы материальных средств на складских площадках позволяют осуществить две отгрузки;
3 – запасы материальных средств на складских площадках позволяют осуществить три отгрузки;
i – запасы материальных средств на складских площадках позволяют осуществить i отгрузок;
s – складские площадки заполнены полностью и позволяют осуществить s отгрузок;
Вероятности состояний системы, представленной на рисунке 1, можно представить в виде дифференциальных уравнений следующего вида
Для общего случая при n партий отгрузки со склада материальных средств в одной партии завозимой на склад
Для установившегося режима функционирования системы массового обслуживания при t→∞dPs/dt=0 дифференциальные уравнения можно представить в виде системы линейных, при этом к системе необходимо добавить условие
где Р0 – вероятность исхода при котором склад окажется пустым.
Значения функции fi(λ,μ) можно вычислить по рекуррентным формулам системы алгебраических уравнений
.В представленном случае вероятность полного заполнения складских площадок – P>s вычисляется по выражению
Соответственно величина усредненных объемов материальных средств хранящихся на складе вычисляется по формуле
Для оценки остальных параметров работы склада возможно применение других методов теории вероятностей с требуемой интерпретацией входных значений параметров и вычисленных результатов.
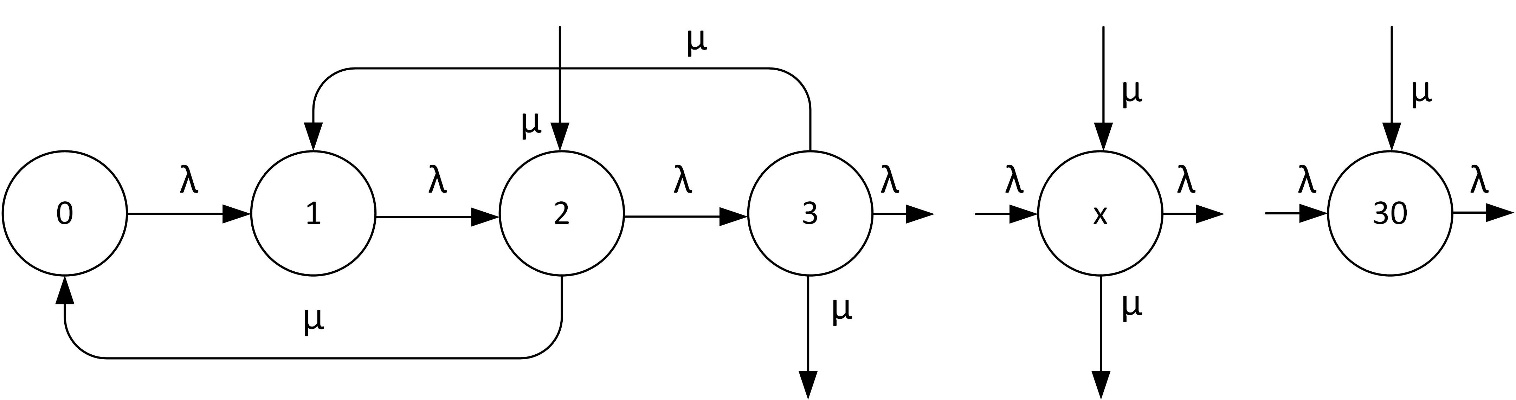
Рисунок 2 - Граф вероятностей состояний складских запасав материальных средств
Примечание: при размере партии выдачи равной двум партиям поставки
Данный пример характерен для тех случаев когда материалы ВСЖП поступают на площадки хранения либо по долгосрочным контрактам, либо со сборочных линий функционирующих в установившемся режиме, с плановыми поставками 15 партий в течении месяца, соответственно λ=0,5 комплектов в сутки. Вывоз партий материальных средств осуществляется при накоплении на складских площадках запасов обеспечивающих их полную загрузку. В том случае когда на склад поступило запасов которыми может быть обеспечена две партии выдачи, подается заявка на подачу очередных транспортных средств. В модели время потребное для подачи транспорта под погрузку равно tn, в этом случае μ=1/tn.
Состояния системы массового обслуживания, изображенной на рисунке 2:
0 – на складских площадках отсутствуют запасы материальных средств;
1 – на складские площадки поступила одна партия;
2 – на складские площадки подано 2 партии, имеется одна заявка на отгрузку;
3 – на складские площадки подано 3 партии, имеется одна заявка на отгрузку;
4 – на складские площадки подано 4 партии, имеется две заявки на отгрузку;
х – на складские площадки подано х партий, имеется Int(х/2) заявок на отгрузку;
30 – на складские площадки подано 30 партий, имеется 15 заявок на отгрузку.
Вероятности состояний системы, представленной на рисунке 2, можно представить в виде дифференциальных уравнений следующего вида
где P31 – вероятность полной загрузки складских площадок, а Р0 - вероятность полного освобождения склада.
Для небольших периодов рационально решать систему дифференциальных уравнений для вероятностей состояния склада заданных входными значениями.
Для установившегося режима функционирования системы массового обслуживания при t→∞ дифференциальные уравнения можно представить в виде системы линейных. При этом данный подход к решению задачи, с использованием рекурсивных формул, осложняется необходимостью рассмотрения системы уравнений, созданной под каждый конкретный случай, при этом число уравнений в системе будет на одно больше чем вместимость складских площадок, в рассматриваемых партиях поставки материальных средств.
Как и в первом случае, для оценки остальных параметров работы склада возможно применение других методов теории вероятностей с требуемой интерпретацией входных значений параметров и вычисленных результатов.
К примеру, средний ожидаемый объем материалов находящихся на складе можно вычислить по выражению
где q – объём 1 партии поставки, метров верхнего строения железнодорожного пути.
3. Заключение
Проведенные расчёты показали, что при дефиците исходных данных и сложности проведения натурного эксперимента с реальными объектами применение описанных в статье моделей позволяет рассчитывать вероятностные параметры, характеризующие организацию складского обеспечения, процессов строительно-восстановительных работ на объектах инфраструктуры железнодорожного транспорта, и оценивать загруженность отдельных складских мощностей, математически обосновывать оптимальное количество потребных площадей хранения. Полученные результаты моделирования позволяют формулировать параметры основных мероприятий, направленных на снижение времени простоя технических средств, задействованных на транспортных и путеукладочных работах, за счет своевременного подвоза материальных средств к местам производства работ.
Предлагаемые модели позволяют обосновать отдельные параметры логистических процессов, выполняемых в ходе производства работ на этапе формирования планов. Таким образом, еще на этапе выработки замысла, могут формироваться обоснованные предложения по включению в состав развертываемых строительных площадок складских зон, ориентированных на их материальное обеспечение. Дальнейшее развитие моделей позволит выполнить обоснование потребных составов команд, задействованных в производстве складских работ.
