MATHEMATICAL MODELING FOR THE WORK OF STEEL-CONCRETE SAMPLES REINFORCED BY CUT AND STRETCHY SHEET
Бурченя С.П.
Burchenia S. P.
асистент, Львовский национальный аграрный университет
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ РАБОТЫ ОПЫТНЫХ СТАЛЕБЕТОННЫХ ОБРАЗЦОВ, АРМИРОВАННЫХ ПРОСЕЧНО-ВЫТЯЖНЫМ ЛИСТОМ
Аннотация
Целью нашего исследования является разработка математической модели изгибаемого сталебетонного опытного образца, армированного просечно-вытяжным листом и получение расчетных значений деформаций бетона и арматуры, которые отвечают экспериментальным данным.
Ключевые слова: математическая модель, сталебетон, просечно-вытяжной лист, деформации.
Key words: mathematical modelling, researched steel-concrete samples, cut and stretchy sheet, deformation.
Широкое использование математических моделей в различных отраслях техники привело к тому, что в конце 50-х гг. ХХ век математическое моделирование сформировалось в самостоятельный метод исследования, который состоит из описания свойств произвольного объекта языком математики с целью последующего исследования этого описания также математическими методами. В широком понимании «моделирование» − это метод познания (исследования), который включает в себя построение модели, ее последующий анализ и интерпретацию полученных результатов [1].
При проектировании зданий и сооружений необходимо разрабатывать специальную методику и технику моделирования. Применять моделирование, для выявления напряженно деформированного состояния строительных конструкций, стали много научно-исследовательских институтов и лабораторий как Украины, так и зарубежных стран: России, Америки, Англии, Франции, Польши, Румынии. Круг задач, которые развязываются с помощью моделирования, очень широкий и касается достаточно важных вопросов проектирования и строительства.
Основные правила моделирования сводятся к следующему:
− модель должна быть геометрически подобна физическому образцу;
− безразмерные начальные и конечные условия в модели должны совпадать с такими же условиями натурального образца;
− одноименные безразмерные параметры, которые входят в математическое уравнения, начальные и конечные условия в модели и физическом образце должны быть соответственно равными [3].
Метод моделирования – один из наиболее рациональных, удобных и доступных методов для опытов и наблюдений. Он даёт возможность экономить средства и материалы, сокращать время исследований, а также на его основе проводить более глубокие и более обширные экспериментальные исследования. Этот метод позволяет обобщать теоретические исследования, использовать полученные результаты не только для одного образца, который моделируется, но и на целую группу образцов и явлений, подобных образцу, изготовлять и повторять такое моделирование в разных масштабах [2].
При разработке математической модели работы изгибаемого опытного сталебетонного образца, армированного просечно-вытяжним листом, аппроксимирующую функциональную зависимость строим методом наименьших квадратов. В нашем случае рассматриваем две опытных сталебетонных балки Б-1 и Б-2, в которых: в первой балке просечно-вытяжной лист размещен в нижней части балки с защитным слоем бетона, в другой балке − без защитного слоя.
При среднеквадратичном приближении мерой отклонения значений аппроксимирующей функции y = (x) от исследуемой эмпирической зависимости определенной на множественном числе точек (xi, yi), (і = 1, …, n) есть величина S, которая равняется сумме квадратов разниц между экспериментальными значениями и значениями аппроксимирующей функции в заданных точках. То есть:
Построение эмпирической зависимости y =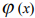
методом наименьших квадратов состоит из трех этапов. На первом этапе определяется вид функциональной зависимости. Преимущество предоставляется самым простым формулам, которые владеют достаточной точностью. Такой предварительный выбор можно осуществить из геометрических соображений. Экспериментальные точки (xi, yi), (і = 1, …, n) наносим на график, определяя общий вид зависимости путем сравнения полученной кривой с графиками известных функций (полиномиальной, степенной, показательной или логарифмической функций).
В результате проведенного анализа графиков исследуемых экспериментальных зависимостей, приближения осуществляем степенной функцией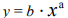 
На втором этапе определяются оптимальные значения параметров а и b выбранной зависимости.
Параметры исследуемой зависимости определяем методом наименьших квадратов как точку минимума функции:
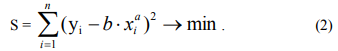
Из необходимого условия экстремума:
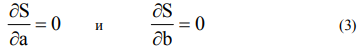
Получаем систему нелинейных уравнений для определения параметров а и b степенной функции:
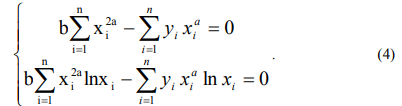
Методом Ньютона с необходимой точностью определяем решение системы (4).
На третьем этапе путем сравнения результатов проводим оценку адекватности выбора эмпирической зависимости.
Сравнение результатов теоретических расчетов деформаций бетона и арматуры, изгибаемых опытных образцов, армированных просечно-вытяжным листом методом наименьших квадратов воспроизведено в виде графиков на рис. 1, 2.
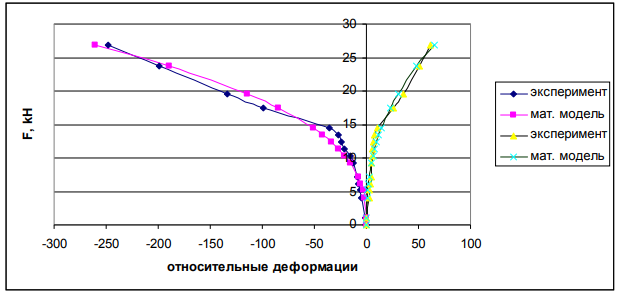
а)
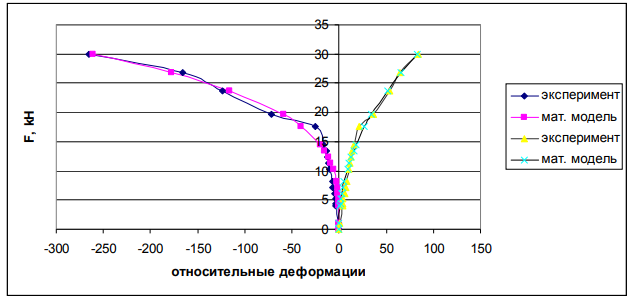
б)
Рис. 1. Графики зависимости относительных деформаций разтяжения и сжатия бетона изгибаемых опытных образцов армированных просечно-вытяжным листом от величины нагрузки: а)балка Б-1; б)балка Б-2.
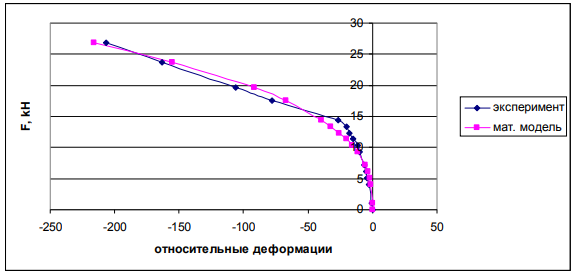
а)
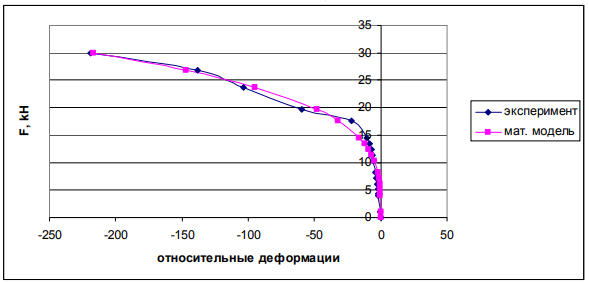
б)
Рис. 2. Графики зависимости относительных деформаций арматуры изгибаемых опытных образцов армированных просечно-вытяжным листом от величины нагрузки: а) балка Б-1; б) балка Б-2.
На основе экспериментально-теоретических исследований работы опытных изгибаемых сталебетонных образцов, армированных просечно-витяжним листом можно сделать следующие выводы:
1. Использование метода наименьших квадратов позволяет построить аппроксимирующую функциональную зависимость при разработке математической модели работы изгибаемых сталебетонных образцов, армированных просечно-вытяжным листом.
2. Построение за такой методикой математической модели работы изгибаемых сталебетонных образцов с рабочей арматурой в виде просечно-вытяжного листа позволяет с достаточной точностью определить деформации бетона и арматуры от начала загрузки образца вплоть до его разрушения. При эксплуатационных уровнях нагрузки, согласно вышеизложеной методике, погрешность расчета составляет 7…15% от экспериментальных данных.