ITERATIVE METHOD OF CALCULATION FOR THIN-WALLED ANISOTROPIC CORES OF OPEN PROFILE ON TORSION

Аллахвердов Б.М.¹, Полинкевич К.Ю.²

¹Кандидат технических наук, доцент,

Петербургский государственный университет путей сообщения императора Александра I г. Санкт-Петербург, Россия

²Аспирант,

Петербургский государственный университет путей сообщения императора Александра I г. Санкт-Петербург, Россия

ИТЕРАЦИОННЫЙ СПОСОБ РАСЧЕТА ТОНКОСТЕННЫХ АНИЗОТРОПНЫХ СТЕРЖНЕЙ ОТКРЫТОГО ПРОФИЛЯ НА КРУЧЕНИЕ

Аннотация

Предлагается описание  методики расчета на прочность тонкостенных анизотропных стержней открытого профиля, основанной на итерационном способе последовательного удовлетворения условиям равновесия и совместности деформаций. На первом цикле итераций получено решение Власова В.З. На последующих циклах получено решение с учетом анизотропии, деформации сдвига и нормальной поперечной деформации. Рассматривается вопрос сходимости результатов. На примере современного углепластика показано как меняются характеристики материала в зависимости от направления армирующих волокон.

Ключевые слова: теория упругости, анизотропия, метод итераций, напряжения, деформации.

Allakhverdov B.M.¹, Polinkevich K.Y.²

¹ PhD in Engineering, lecturer,

Petersburg State University of Railways of Emperor Alexander I St. Petersburg, Russia

² Postgraduate student,

Petersburg State University of Railways of Emperor Alexander I St. Petersburg, Russia

ITERATIVE METHOD OF CALCULATION FOR THIN-WALLED ANISOTROPIC CORES OF OPEN PROFILE ON TORSION

Abstract

The article provides the description of the calculation technique which determines the strength of thin-walled anisotropic cores of an open profile based on an iterative method of successive accordance with the conditions of equilibrium and deformations compatibility. The first cycle of iterations allowed us to obtain V.Z.Vlasov solution. In subsequent cycles, we obtained the solution which takes into account the anisotropy, the deformation of the shift and normal transverse deformation. The question of the results convergence is studied in the article. The example based on modern carbon fiber illustrates how the material characteristics differ depending on the direction of the reinforcing fibers.

Keywords: elasticity theory, anisotropy, iterative method, stress, deformation.

Задача о кручении изотропного тонкостенного стержня открытого профиля без учета сдвигов решена В.З. Власовым [1]. Для уточнения этого решения используется метод итераций [2], [3] основанный на последовательном удовлетворении условиям равновесия и совместности деформаций. Аналогичный путь решения  распространен на стержни, выполненные из анизотропных материалов [4].

Предварительный этап

Будем считать, что поперечное сечение тонкостенного стержня открытого профиля состоит из n анизотропных пластин толщиной t_i, жестко соединенных между собой вдоль длинных ребер. (рис.1). В качестве основной принимается гипотеза недеформируемости контура поперечного сечения.

Стержень закручивается заданным крутящим моментом М. При этом функция углов закручивания  поперечных сечений по длине стержня подлежит определению.

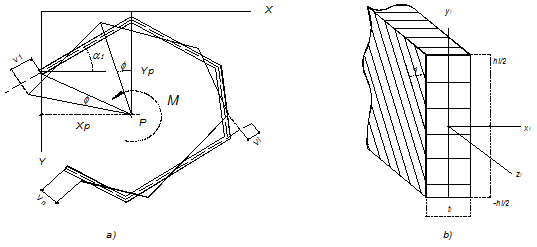
Рис. 1.

а) Поперечное сечение тонкостенного стержня открытого профиля

(до и после поворота на угол φ).

б) Один из анизотропных элементов сечения (главные оси анизотропии под углом α к оси y_i)

Для всего стержня выбирается произвольная глобальная система координат Х, Y. Координата Z направлена вдоль оси стержня (рис.1.а). В то же время для каждого i –го элемента вводится местная координатная система x_i, y_i, z_i (рис.1.б). При кручении любое сечение стержня с координатой z поворачивается на угол  относительно центра кручения Р, имеющего координаты Хр, Yр подлежащие определению. При таком повороте каждый элемент перемещается как в своей плоскости, так и из плоскости.  Перемещения V_i в плоскости y_i, z_i соответствуют изгибу элемента, перемещения же из плоскости вызваны кручением этой пластины.

Перемещения V_i отдельной пластинки можно описать через координаты центра кручения X_p, Y_p и угол закручивания поперечных сечений относительно этого центра :

                        (1)

где r_i – нормаль к оси i –ой пластинки, проведенная из точки P.

 Таким образом кривизна i элемента в его плоскости становится функцией:

                                                  (2)

Считается, что пластины выполнены из различных анизотропных материалов, упругие свойства которых обычно задаются в главных осях анизотропии у, z (вдоль и поперек волокон материала). Обобщенный закон Гука для случая плоского напряженного состояния принимает следующий вид:

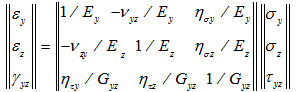                                        (3)

Здесь E_y, E_z, G_yz - соответственно модули упругости и сдвига;

ε_z, ε_y – относительные удлинения (линейные деформации) в направлении действия нормальных напряжений;

γ_yz - относительный сдвиг - величина изменения прямого угла между площадками, на которых действуют соответствующие касательные напряжения;

ν_zy, ν_уz  – коэффициенты  влияния  линейной деформации по направлению z  на линейную деформацию по направлению у и наоборот, при этом соблюдается отношение .

η_σ,y, η_σ,z , η_t,y, η_t,z – коэффициенты  влияния  линейной деформации на  сдвиговую деформацию   по направлениям z, у и наоборот; при этом соблюдаются отношения  и .

В случае, если при заданных для некоторой системы координат у, z упругих постоянных требуется найти упругие постоянные для новой системы y1, z1, повернутой по отношению к первой на угол α (рис.1 б), модули и коэффициенты для новых осей определяются по формулам, приведенным в [2]:

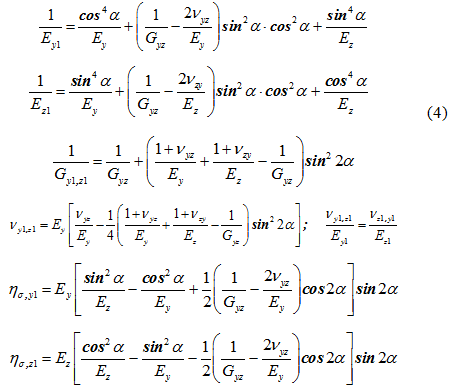
На рис.2 показаны графики зависимости модуля упругости и модуля сдвига углепластика марки M60J/Epoxy [5] от угла поворота осей анизотропии.

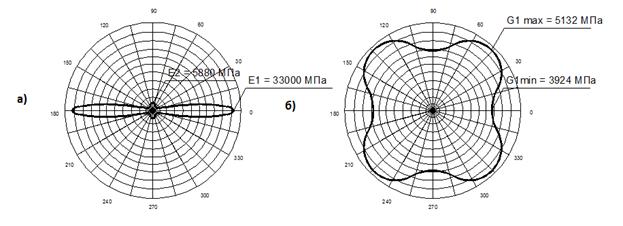
Рис.2 - Полярные диаграммы изменения модулей углепластика M60J/Epoxy при повороте координатных осей:

а) продольной упругости;

б) сдвига

Цикл 1.

1. Первое приближение (первый шаг итераций).

1.1. Принимаем на первом этапе для каждой i –ой пластины анизотропный материал со следующими упругими характеристиками: E_zi (та же величина, что и в реальном материале); остальные модули стремятся к бесконечности E_yi= ∞; G_yzi=∞. В этом случае закон Гука имеет вид:

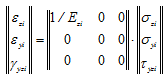                                                      (5)

1.2. При таком виде закона Гука ,

что соответствует гипотезе о ненадавливании волокон.

1.3. Тогда . 1.4. Также из (5) . 1.5. Тогда , 1.6. и  (6)

Получена известная в сопротивлении материалов зависимость - гипотеза плоских сечений (отдельно для каждого элемента), где и  неизвестные функции. Здесь  можно трактовать как продольную деформацию оси стержня, а - как кривизну его оси.

При этом на гранях пластин должны соблюдаться условия совместности деформаций:  - так выглядят эти условия между двумя соседними пластинами (индекс к означает деформацию волокна , индекс н - . деформацию волокна ).

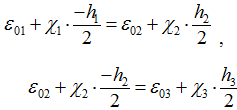- между второй и третьей и т.д.

1.7. Продольная деформация оси любой пластины выражается через продольную деформацию оси первой из них (похожая идея высказана в [3]):

                             (7)

Выражение (7) содержит четыре неизвестных величины: Xp, Yp,   Для их определения следует составить глобальные уравнения равновесия.

1.8. Первое уравнение  позволяет определить функцию (z).

1.9. Два других уравнения  служат для определения координат центра кручения Xp, Yp.

Здесь следует учесть, что изгибающий момент в плоскости каждой пластины записывается так:

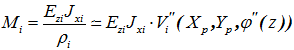                (8)

1.10. Возникающие в элементе поперечные силы представляются в следующем виде:

,                (9)

1.11. Поперечные силы создают часть крутящего момента, вызванного изгибом элементов (то, что у Власова [1] названо моментом стесненного кручения):

                  (10)

Здесь   - плечо силы по (2).

1.12. Вторая составляющая крутящего момента связана с свободным кручением каждой пластины:

                                                          (11)

1.14.  Уравнение равновесия , из которого можно найти функцию угла закручивания , становится дифференциальным уравнением:

                               (12)

где   - аналог секториальной жесткости по [1], -   крутильная жесткость, что повторяет уравнение В.З. Власова [1].

Решив его при заданных граничных условиях, зависящих от способов закрепления стержня, получаем функцию углов закручивания .

На этом заканчивается определение неизвестных первого этапа.

1.15. Далее на этом этапе окончательно определяется функция нормальных напряжений в каждом элементе .

1.16. Из уравнения равновесия 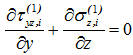 определяется функция касательных напряжений:

.                             (13)

Здесь, согласно теореме Бредта, поток касательных напряжений на границе элементов сохраняется т.е. . Исходя из этого условия, и зная, что на свободных гранях отсутствуют касательные напряжения, определяются произвольные функции 

1.17. Из второго уравнения равновесия 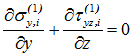 определяется функция поперечных нормальных напряжений:

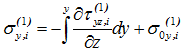.                               (14)

Теперь, если по теореме Бредта, поток касательных напряжений на границе элементов сохраняется, то также должен сохраняться поток поперечных нормальных напряжений: .   Исходя из этого условия, и зная, что на свободных гранях отсутствуют эти напряжения, определяются произвольные функции .

Следует обратить внимание на следующие факты – в этом цикле:

• Продольные нормальные напряжения по высоте –линейные функции в пределах каждого элемента.
• Продольные нормальные напряжения по длине –являются функциями, зависящими от .
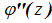• Касательные напряжения по высоте –квадратные параболы в пределах элемента.
• Касательные напряжения по длине –являются функциями, зависящими от .
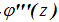• Поперечные нормальные напряжения по высоте –кубические параболы в пределах элемента.
• Поперечные нормальные напряжения по длине –являются функциями, зависящими от .

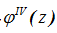На определении напряженного состояния заканчивается первый цикл итераций.

Цикл 2.

На втором цикле остается та же гипотеза неизменяемости контура и все предпосылки первого цикла. За неизвестные также принимаются:

• Функция углов закручивания стержня 
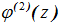
• Координаты центра кручения Хр, Yр.
• Продольная деформация оси элементов 
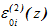
• Кривизна оси элементов 

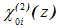
Здесь и далее ⁽²⁾ –принадлежность второму циклу, ⁽¹⁾ –принадлежность первому.

Матрица модулей принимает обычный вид по (5):

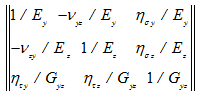
В этом варианте учтено влияние сдвигов и поперечных нормальных напряжений на общее напряженное состояние стержня при кручении.

В начале второго цикла по закону Гука для анизотропного тела (5) находим для каждого элемента функцию деформаций вдоль оси x -  :

                      (15)

Зная функцию деформации , можно найти соответствующую функцию перемещения , пользуясь уравнением связи между деформациями и перемещениями:

                                                         (16)

с точностью до произвольной функции .

Далее определяется функция деформации сдвига по обобщенному закону Гука (5):

          (17)

Затем вновь находим функцию продольных деформаций  по процедуре, описанной в первом цикле:

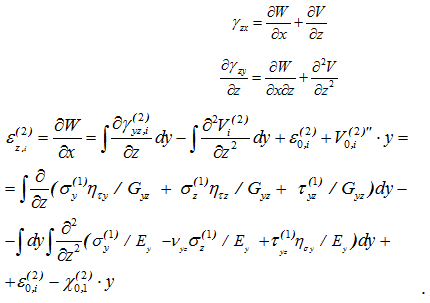            (18)

Продольная деформация (17) состоит из двух частей: последние два слагаемых повторяют линейное распределение этой деформации по высоте элемента на первом цикле и зависят от производных функции , первые же слагаемые создают более высокий порядок распределения по высоте, соответствующий напряжениям, определенным на первом этапе - они зависят от производных функции .

Все дальнейшие вычисления ведутся по последовательности, изложенной выше для первого цикла, причем для величин, зависящих от , решение сводится к тому же виду дифференциального уравнения (12). Однако величины, зависящие от уже определенной функции , будучи перенесенными в правую часть этого уравнения, играют роль увеличения или уменьшения величины заданного крутящего момента. Таким образом уравнение (12) трансформируется в следующее:

                 (19)

с теми ж граничными условиями, как и на первом цикле.

Дальнейшие уточнения решения (следующие циклы) проводятся в той же последовательности.

Как следует из вышеизложенного, на каждом этапе при вычислении напряжений происходят операции дифференцирования по координате z и интегрирования по координате у. Такой подход к задаче определения напряжений приводит результату, представленному в табл.1.

Табл. 1

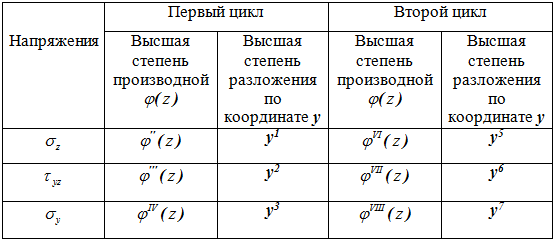
На этих фактах базируется сходимость данного итерационного процесса -  при увеличении циклов до числа m напряженное состояние по длине стержня l зависит от возрастания степени производных функции , т.е. приращение напряжений пропорционально величине 1/l ^2m. С другой стороны напряженное состояние по высоте стержня h с доведением числа циклов до m характеризуется увеличением влияния высоты элементов в виде h^2m. Следовательно на каждом цикле можно оценивать добавку к первоначальному решению пропорциональной величине (h/l)^2m.

При отношении h/l=1/3 на втором цикле поправка к напряжениям  пропорциональна величине (1/3)⁴ =0.012, а на третьем уже 0.15^-4. Процесс вычисления напряжений имеет высокую скорость сходимости, обычно достаточно 2 – 3 циклов, чтобы получить необходимую точность решения.

Список литературы / References

1. Власов В.З., Тонкостенные упругие стержни, Стройиздат, 1940 г.
2. Аллахвердов Б.М. Итерационный метод расчета балок с изменяющимися по высоте характеристиками. Исследования по механике материалов и конструкций.(сб. научн.статей)/Вып.12/ Петерб. Гос. Универ. Путей сообщ. –СПб,2002.-С.30 –34, Деп. ВИНИТИ.№ 1400-В2002.
3. Полинкевич К.Ю. Итерационный способ расчета слоистых балок на прочность. Известия Петербургского университета путей сообщения. /Вып 2 (35)/ Петерб. Гос. Универ. Путей сообщ. –СПб,2013.-С.148 –153
4. Аллахвердов Б.М. Полинкевич К.Ю. Итерационный способ расчета анизотропной балки на прочность. Известия Петербургского университета путей сообщения. /Вып 2 (39)/ Петерб. Гос. Универ. Путей сообщ. –СПб,2014.-С.73 –79
5. Попов А.А. Сопротивление материалов (теория и задачи). Государственное научно-техническое издательство машиностроительной литературы. Москва, 1956, стр. 476.
6. Лехницкий С.Г. Анизотропные пластинки. Государственное издательство технико-теоретической литературы. Москва, 1957, стр. 463.

Список литературы на английском языке / References in English

1. VZ Vlasov, Tonkostennie uprugie stergni [Thin walls elastic beams], Stroiizdat [construction publishing], 1940.
2. BM Allakhverdov. Iteracionnii metod rascheta balok s izmenyaushimisya po visote harakteristikami [Iterative method of calculation of beams with variable height characteristics]. Issledovaniya po mechanike materialov I konstrukcii (sb. nauchn. statei)/Vip 12/ Peterb. Gos. Univer. Putei soobch. [Research on the mechanics of materials and structures.(collected scientific articles)/Edd.12/ Petersburg. The State University of Communications. St. Petersburg]. –SPb,2002.-P.30 –34, Dep. VINITI.№ 1400-В2002.
3. KY Polinkevich. Iteracionnii sposob rascheta sloistich balok na prochnost’[An iterative method of calculation of layered beams for strength] Izvestiya Peterburgskogo universiteta putei soobcheniya [Proceedings of the St. Petersburg University of Railways]. / Issue 2 (35) / Petersburg State University of Railways. SPb, 2013.-p.148 -153
4. BM Allakhverdov, KY Polinkevich. Iteracionnii sposob rascheta anizotropnoi balki na prochnost’[The iterative method of calculation of the anisotropic beam strength] Izvestiya Peterburgskogo universiteta putei soobcheniya [Proceedings of the St. Petersburg University of Railways]. / Issue 2 (39) / Petersburg State University of Railways. SPb, 2014.-p.73 -79
5. AA Popov. Soprotivlenie materialov (teoriya I zadachi) [Strength of Materials (theory and tasks).]. Gosudarstvennoe nauchno-technicheskoe izdatel’stvo mashinostroitel’noi literature [State scientific and technical publishing engineering literature]. Moscow, 1956, P. 476.
6. SG Lekhnickii. Anizotropnie plastinki [Anisotropic plates]. Gosudarstvennoe izdatel’stvo techniko-teoreticheskoi literature [State Publishing House technical and theoretical literature]. Moscow, 1957, P. 463.