THE ANALYSIS OF METHODS OF REFINEMENT OF THE FINITE ELEMENT MODEL AFTER TOPOLOGY OPTIMIZATION

Кротких А.А.¹, Максимов П.В.²

¹студент, Пермский национальный исследовательский политехнический университет;

²кандидат технических наук, доцент, Пермский национальный исследовательский политехнический университет

Работа выполнена при финансовой поддержке Министерства образования и науки РФ (договор №02.G25.31.0168 от 01.12.2015 г. в составе мероприятия по реализации постановления Правительства РФ № 218).

ИССЛЕДОВАНИЕ И МОДИФИКАЦИЯ МЕТОДА ТОПОЛОГИЧЕСКОЙ ОПТИМИЗАЦИИ SIMP

Аннотация

Настоящая статья посвящена исследованию алгоритма топологической оптимизации SIMP. Алгоритм был воспроизведен, проанализирован в вычислительно пакете Wolfram Mathematica. Был обнаружен недостаток данного метода, который представлял собой определение оптимального коэффициента Лагранжа. Авторами предложен и исследован вариант модифицированного алгоритма SIMP, который исключает проблему поиска подходящего коэффициента. Предложенный вариант алгоритма был сравнен с изначальным, и было показано, что результат использования модифицированного алгоритма лучше чем результат обычного метода SIMP. Минусом модификации является увеличение времени счета алгоритма.

Ключевые слова: SIMP, топология, оптимизация формы..

Krotkikh A.A.¹, Maksimov P.V.²

¹ student, Perm National Research Polytechnic University;

² PhD in Engineering, associate professor, Perm National Research Polytechnic University

THE ANALYSIS OF METHODS OF REFINEMENT OF THE FINITE ELEMENT MODEL AFTER TOPOLOGY OPTIMIZATION

Abstract

This article is dedicated to the study of topological optimization algorithm SIMP. The algorithm has been reproduced and analyzed iby Student Edition Wolfram Mathematica 11.0.1. Disadvantage of this method has been discovered. It was a problem of determining Legrange coefficient. The authors have proposed and examined a variant of the modified algorithm SIMP, which eliminates the problem of finding a suitable Legrange coefficient. The proposed version of the algorithm has been compared with the original, and it was shown that the result of using the modified algorithm is better than the result of normal SIMP. The weakness of the modified algorithm is a computing time.

Keywords: SIMP, topology, optimization of shape.

Работа посвящена исследованию метода топологической оптимизации (SIMP метод), целью которого является снижение податливости всей конструкции за счет перераспределения материала в области, ограниченной телом либо заданной нами. Это позволяет получать объекты, которые имеют специфические свойства при заданных ограничениях[1, С. 3]. Используется в аддитивных технологиях, так называемых технологиях 3D печати, позволяющие получать тела заданной формы. Используя метод, мы можем получить максимально прочные конструкции практически для любой решаемой задачи. Результатом использования метода также является получение равнопрочного объекта в рамках рассматриваемой задачи. Основной идеей метода является создание поля виртуальной плотности, которая представляет аналог какой-то реальной характеристики тела, например, при решении двумерной задачи оптимизации виртуальная плотность выполняет роль толщины тела в этой точке.

Применим метод SIMP к плоской задаче теории упругости. Имеется тело, на которое действуют внешние силы, также оно закреплено некоторым образом. При заданных краевых условиях задача решается  методом конечных элементов.

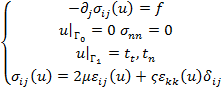                                           (1)

В МКЭ будем использовать симплекс элемент – треугольный элемент с линейной Лагранжевой аппроксимацией. Результатом решения будет некоторая деформированная модель объекта. На базе результата МКЭ мы применяем метод SIMP, который заключается в определении оптимального поля виртуальной плотности тела. Изначально поле плотности задается однородным. Это означает, что плотность одинаковая и равна ρ = 1. Целевой функцией, которую мы будем оптимизировать по выбранному параметру, будет податливость объекта. Необходимо достигнуть минимальных перемещений в узлах конечно-элементной сетки. Таким образом, мы минимизируем целевую функцию податливости как функцию виртуальной плотности. Алгоритм оптимизации и целевая функция (2) выбраны на основе работы [2, C. 3]

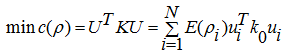                                    (2)

                                                           (3)

При необходимости можно задать ограничение на массу и объем, занимаемый будущей конструкцией, и определить диапазон изменения виртуальной плотности. Алгоритм определения плотностей представлен в работе [2, C. 3].

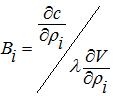                                                                   (4)

где B (4) - условие оптимизации, λ-коэффициент Лагранжа

                                                     (5)

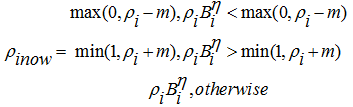                               (6)

Используя такой алгоритм, мы сможем получить каноничное решение SIMP метода, представленное в виде черно-белого решения [1, C. 5, 2, C. 5, 3, C. 4, 4, C.39]. Сформулируем задачу для МКЭ и применим к результату метод SIMP. Дана плоская прямоугольная область, защемленная на правой границе. На левой границе в верхнем углу приложена сосредоточенная нагрузка.

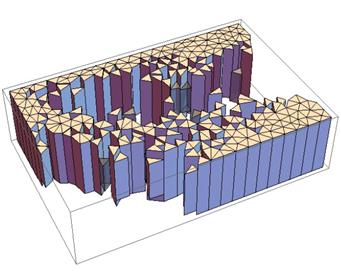
Рис. 1 – «Черно-белое» решение SIMP метода

Недостатком SIMP метода является его результат: получение несвязной области (Рис.1), что противоречит здравому смыслу задачи. Для этого используется алгоритм распределения плотности по близлежащим конечным элементам (Рис.2), также называемый алгоритмом фильтрации. Вводится вектор Н (7,8), который содержит в себе значения расстояний от центра текущего КЭ до центра всех КЭ, удовлетворяющих заданным условиям, в области. В данной задаче КЭ должны лежать в пределах критического радиуса влияния.

                                                                   (7)

                                         (8)

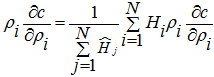                                                     (9)

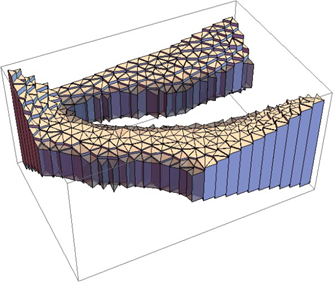
Рис. 2 – Результат использования фильтрации

Второй проблемой метода является определение множителя Лагранжа для получения корректной оптимизации объекта. Для каждого выбранного нагружения и формы объекта необходимо подобрать свой коэффициент Лагранжа. От этого коэффициента зависит и «физичность» решения, и границы применимости метода для каждой конкретной задачи. То есть, неправильно определив значение коэффициента, мы можем получить абсолютно некорректное решение. Примером такого решения может послужить «острова» материала с максимальной допустимой плотностью. Авторы работы предлагают усовершенствовать исходный алгоритм метода SIMP, введя изменения в определение вектора B (10,11). Таким образом мы устраним проблему определения коэффициента оптимизации.

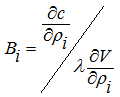                                                       (10)

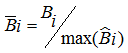                                                   (11)

Алгоритм изменения плотности также был изменен, и приобрел такой вид (12):

                                                       (12)

Необходимо оценить насколько адекватной является данная корректировка метода. Сравним изменения перемещения нескольких реперных точек при использовании метода SIMP с коэффициентом Лагранжа и с коэффициентами, вычисленными модифицированным методом. Реперные точки выбраны таким образом, чтобы охарактеризовать перемещения в опасных участках модели, в данном случае это точки, лежащие в окрестности нагружения. Необходимо также удостовериться в том, что модифицированный метод не обнуляет значение виртуальной плотности в конечных элементах, к которым относится реперная точка. Таким образом, получается, что в ходе решения задачи мы каждый раз находим такие B_i, которые наилучшим образом подходят под данную форму объекта. Необходимо также показать, что такой вариант алгоритма не приводит к ухудшению итогового решения и получает некоторое сходящееся решение как изначальный SIMP метод.

На нижеприведенных графиках (Рис.3,4) видно, что при увеличении коэффициента Лагранжа расстояния между кривыми, характеризующими перемещения в реперной точке, уменьшаются. Модифицированный алгоритм сразу «подбирает» коэффициент таким образом, чтобы получить результат, к которому будут стремиться решения с постоянным коэффициентом. Стоит сказать, что бесконечное увеличение коэффициент Лагранжа не даст нам сразу итоговое решение. Решение будет получаться до тех пор пока первая итерация метода SIMP дает «физически-верное» решение. Имеется ввиду, что в решение не будут присутствовать «острова» материала не связанные с остальной областью. Если получится «физически-неверное» решение, «остров» материала не будет связан с граничными условиями по закреплениям и будет ничем неограничен в перемещениях. То есть, на графиках перемещений у нас такое решение даст бесконечный рост перемещения относительно начального. Таким образом, мы исключаем проблему определения границ значений для коэффициента оптимизации. Минус модифицированного метода заключается в том, что для его реализация требует больше вычислительных ресурсов, нежели оригинальный метод SIMP. Это связано с тем, что мы переопределяем функцию чувствительности и изменяем алгоритм изменения виртуальной плотности. В итоге метод требует несколько больше итераций чем оригинальный.

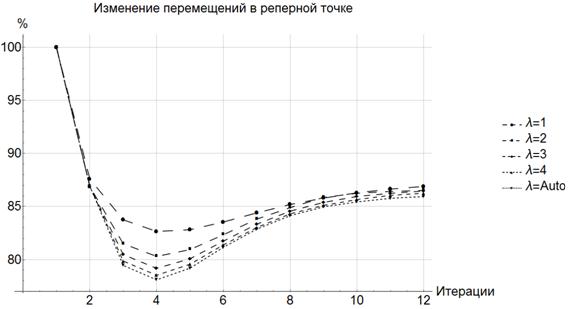
Рис. 3 – Сравнение перемещений в реперной точке №95 при использовании различных коэффициентов Лагранжа и модифицированного метода

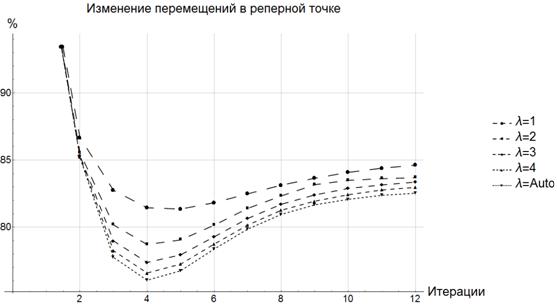
Рис. 4 – Сравнение перемещений в реперной точке №72 при использовании различных коэффициентов Лагранжа и модифицированного метода

В заключении необходимо подчеркнуть, что корректировка метода SIMP не отменяет его абсолютной сходимости к некоторому конечному решению. Математическое обоснование и доказательство этого факта предложено в работе [4, C. 29], результаты оптимизации схожи с результатами других автором, несмотря на то, что используется другой тип КЭ.

Таким образом, авторами работы были достигнуты следующие результаты:

• Был воспроизведен метод SIMP в чистом виде, т.е. с «шахматной доской» и без.
• Была проанализирована адекватность метода путем сравнения методом конечных элементов перемещений в реперных точках.
• Был предложен модифицированный метод SIMP и продемонстрирована его адекватность в сравнении с оригинальным методом SIMP при различных значениях коэффициента Лагранжа.

Список литературы / References

1. Brackett D.J., Ashcroft I.A. and Hague R: Topology optimization for additive manufacturing, 22nd Annual International Solid Freeform Fabrication Symposium, Texas, USA, 348-362, 2011
2. Jun-ichi Koga., Checkerboard Problem to Topology Optimization of Continuum Structures/ Jun-ichi Koga., Jiro Koga, Shunji Homma., Computational Engineering, Finance, and Science – 2013
3. Diaz A., Checkerboard Patterns in Layout Optimization/ Diaz A., Sigmund, O., Structural and Multidisciplinary Optimization – 1995 – Issue 1 – 40-45
4. Bondsoe M.P. Topology Optimization Theory, Methods and Applications/ Bondsoe M.P., Sigmund O., Topology Optimization – Berlin, Springer-Verlag Berlin Heidelberg GmbH, 2002.