REPRESENTATION OF FUZZY RULES BASE AS A HIERARCHY BY GROUPING OF RULES
Research article
Published:
2014/02/08
Сергиенко М.А.
Кандидат технических наук,
Воронежский государственный университет
ПРЕДСТАВЛЕНИЕ НЕЧЕТКОЙ БАЗЫ ПРАВИЛ В ВИДЕ ИЕРАРХИИ НА ОСНОВЕ ГРУППИРОВКИ ПРАВИЛ
Аннотация
В статье рассмотрен алгоритм представления базы нечетких правил в виде иерархии, в которой каждый элемент не нулевого уровня представляет собой агрегированное правило из его потомков (дочерних правил). Группировка правил осуществляется на основе вычисления степени важности правила (рейтинга) по отношению к другим правилам. Такое представление базы правил позволяет оперировать не всем набором правил, а только определенной частью (правилами одного уровня). В подобной иерархии каждый уровень позволяет получать результат с соответствующей степенью точности, причем каждый следующий уровень зависит от предыдущего. Ключевые слова: нечеткая база правил, рейтинг правила, агрегирование.Sergienko M.A.
PhD in Technical Sciences,
Voronezh State University
REPRESENTATION OF FUZZY RULES BASE AS A HIERARCHY BY GROUPING OF RULES
Abstract
The article considers algorithm of representation fuzzy rules base as a hierarchy. Each element of hierarchy (not zero level) represents an aggregated rule of his descendants (children rules). Grouping of rules is based on calculating importance degree of the rule (rating) with respect to other rules. Such a representation of the fuzzy rules base allows to operate a set of rules (not all rules), but only a certain part (one level rules). Each level of hierarchy allows to obtain results with the appropriate degree of accuracy; each level depends on the previous one. Keywords: fuzzy rule base, rule rating, aggregation. Рассмотрим базу нечетких «если-то» правил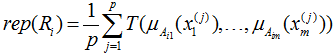 ,
,
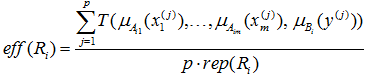 .
.
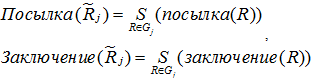 где S – треугольная конорма.
Рассмотрим пример получения обобщенного правила.
Пусть
где S – треугольная конорма.
Рассмотрим пример получения обобщенного правила.
Пусть 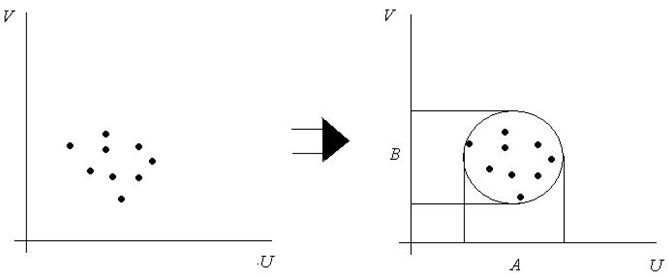
Рис. 1 - Агрегирование правил
На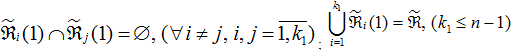 .
Элементами множества
.
Элементами множества 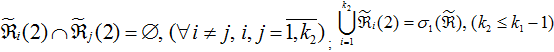 .
Элементами множества
.
Элементами множества 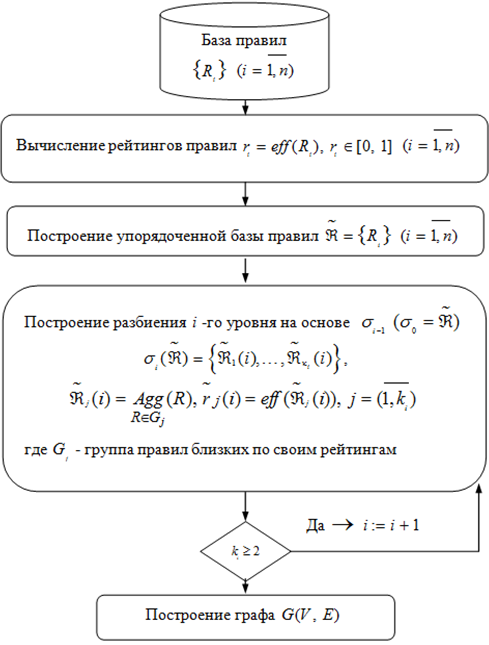
Рис. 2 - Алгоритм представления базы правил в виде некоторого графа
Таким образом, нечеткую базу правил можно представить в виде иерархической структуры, а именно в виде некоторого бесконтурного неориентированного графа- V – множество вершин графа, каждая вершина – это нечеткое правило.
- E – множество ребер графа, каждое ребро соединяет вершины соседних уровней.
- Существует разбиение вершин на уровни
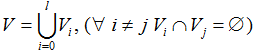 ,
где
,
где - Правила в рамках уровня упорядочены по значениям их рейтингов.
- Вершины одного уровня не смежны.
Литература
- Леденева Т.М. Обработка нечеткой информации: учебное пособие. – Воронеж: Воронежский государственный университет, 2006. – 233 с.
- Кофман А. Введение в теорию нечетких множеств. – М.: Радио и связь, 1982. – 432 с.
