A LEVENBERG-MARQUARDT ALGORITHM EXECUTION TIME REDUCING IN CASE OF LARGE AMOUNT OF THE DATA

Пархоменко С. С.

Аспирант,

Воронежский Государственный Университет

О СОКРАЩЕНИИ ВРЕМЕНИ ОБРАБОТКИ БОЛЬШОГО КОЛИЧЕСТВА ДАННЫХ НЕЙРОННЫМИ СЕТЯМИ МЕТОДОМ ЛЕВЕНБЕРГА-МАРКВАРДТА

Аннотация

Для достижения высокой точности обучения нейронной сети часто применяют алгоритм Левенберга-Марквардта. Однако алгоритм требует построения матрицы Якоби, занимающей много времени. В статье рассмотрены подходы к повышению скорости работы алгоритма Левенберга-Марквардта в рамках обучения нейронной сети.

Ключевые слова: Матрица Якоби, нейронная сеть, активационная функция.

Parkhomenko S. S.

Postgraduate student,

Voronezh State University

A LEVENBERG-MARQUARDT ALGORITHM EXECUTION TIME REDUCING IN CASE OF LARGE AMOUNT OF THE DATA

Abstract

The Levenberg-Marquardt algorithm achieves a high accuracy in a neural network training. However, it requires a time-consuming calculation of a Jacobian matrix. This article is about approaches to the performance improvement of the Levenberg-Marquardt algorithm.

Keywords: Jacobian matrix, artificial neural network, activation function.

Нейронная сеть — универсальный аппроксиматор. Точность аппроксимации зависит от эффективности процедур обучения, поэтому при использовании нейронных сетей в прикладных задачах большое внимание уделяется методам, которые позволяют максимально точно «подстроить» весовые коэффициенты в зависимости от обучающей выборки.

Формально решается оптимизационная задача вида:

,

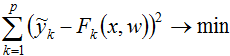где  — полученное значение k-го выхода нейросети при подаче на нее одного из входных образов обучающей выборки;  — желаемое (целевое) значение k-го выхода для этого образа.

Для решения такой задачи широко применяется метод Левенберга-Марквардта, использующий аппроксимацию кривой методом наименьших квадратов, с применением матрицы Гессе в вычислениях. В основе метода лежит уравнение [1, 2, 3]:

,

где J — матрица Якоби для этой системы, H — матрица Гессе,  λ— коэффициент затухания Левенберга (обычно, начальное значение λ достаточно мало, например, 0.1), δ — вектор, состоящий из величин изменений весов,  — вектор, содержащий величину ошибки для каждого обучающего вектора. Элементы вектора  определяют величины изменения соответствующих весов.

Вычисления по методу Левенберга-Марквардта условно можно разделить на две части: матричные расчёты (поиск  ) и поиск вектора изменения весовых коэффициентов δ.

Рассмотрим работу нейросети как вычисление нелинейной функции F(x, w), где  w — вектор весов. Элементы вектора w обычно упорядочиваются сначала по слою, затем по нейронам, и, наконец, по весу каждого нейрона и его смещению.

Матрица Якоби — матрица всех частных производных первого порядка вектор-функции. В случае с нейросетями, это матрица размерностью N×W, где N — количество векторов обучающей выборки,  W — общее количество оптимизируемых параметров (весов и их смещений), содержащая частные производные функции F(x, w) по каждому весовому коэффициенту:

,

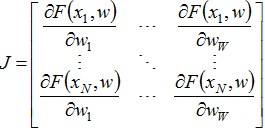где  — вычисленное нейросетью значение по i-ой обучающей выборке с вектором весов  w.

Чаще всего для поиска матрицы J используют различные вариации разностных формул расчёта производных. Самый популярный вариант — центральная разностная производная [4]:

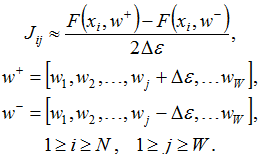
Преимуществом данного метода является универсальность. Его можно реализовать так, что он будет работать независимо от сложности нейронной сети и используемых активационных функций. К недостаткам относятся достаточно низкая производительность и высокие погрешности (особенно при достижении локального или глобального минимума). Для повышения точности можно воспользоваться более сложными формулами, например [4]:

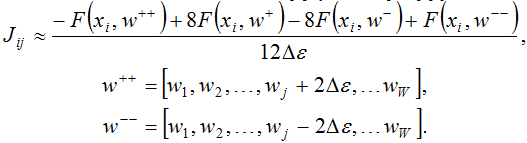
Однако, зачастую они увеличивают количество вычислений функции F(x, w), что снова отрицательно сказывается на производительности.

В случае с нейронной сетью с одним скрытым слоем и одним выходным нейроном, функция F(x, w) будет иметь вид:

,

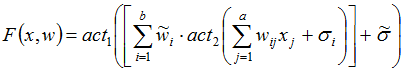где  — принимаемая j-ым входным нейроном величина,  — весовой коэффициент, связывающий j-ый входной нейрон с i-ым нейроном скрытого слоя,  — коэффициент смещения для i-го нейрона скрытого слоя,  — весовой коэффициент, связывающий i-ый нейрон скрытого слоя с выходным нейроном,  — коэффициент смещения для выходного нейрона,  — активационные функции для выходного нейрона и нейронов скрытого слоя соответственно, a — количество входов, b — количество нейронов в скрытом слое. В качестве активационной функции рассмотрим широко используемую сигмоидальную функцию, в силу её монотонного возрастания, непрерывности и дифференцируемости:

.

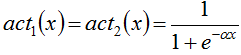С точки зрения вычислительного процесса, на функцию  затрачивается больше времени, чем на все оставшиеся арифметические операции. При этом необходимо учитывать, что для получения одного значения функции F(x, w) необходимо (b+1) раз вычислить значение активационной функции. Если для заполнения матрицы Якоби воспользоваться разностными формулами, то на одну матрицу потребуется подсчитать 2NW(b+1) значений. Важно отметить, что это количество зависит от количества данных в обучающей выборке, которое может быть достаточно большим.

При вычислении матрицы Гессе удобно пользоваться формулой , которая выводится из предпосылок:

 

• функция F(x, w) имеет невысокий порядок нелинейности: вторые производные 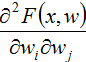 принимают не очень большие значения;
• матрица H рассматривается в малой окрестности минимизирующего вектора w, для которого значения F(x, w) близки к желаемому 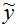, т. е.  .

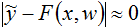При эффективной реализации операции скалярного произведения матриц (в данном случае самой на себя), поиск H обычно не отнимает много времени.

Время вычисления вектора изменения весовых коэффициентов δ зависит только от их количества W, которое определяет число неизвестных переменных в системе линейных уравнений. Однако, как показывают эксперименты, в процессе поиска оптимального δ редко требуется решить более 3-х систем за одну итерацию, что при условии N<<W оказывает незначительное влияние на общее время выполнение алгоритма Левенберга-Марквардта.

Таким образом, можно утверждать, что расчёт матрицы Якоби по времени занимает большую часть работы алгоритма Левенберга-Марквардта [5], а, следовательно, любые подходы, сокращающие затраты на поиск матрицы J, приводят к более быстрому выполнению одного шага обучения нейронной сети.

Один из таких подходов заключается в отказе от расчёта максимально точной матрицы J и использовании её приближенного варианта. Так, например, метод Бройдена позволяет получить матрицу , основываясь на , рассчитанной на шаге n, с помощью формулы [6]:

.

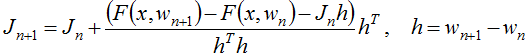С теоретической точки зрения было бы разумно использовать этот подход на каждом шаге работы алгоритма Левенберга-Марквардта, однако на практике, с течением времени аппроксимация становится грубее, что в свою очередь влияет на вектор-градиент  и делает необходимым повторный пересчёт матрицы Якоби более точными методами. Эту операцию можно проводить после каждой неудачной подборки вектора  δ [5].

Вычисление частных производных аналитическим способом несомненно повышает точность вычислений. При этом, благодаря математическим преобразованиям и заменам, возможно сокращение процесса вычислений за счёт повторного использования промежуточных данных, что ведёт к уменьшению количества вызовов сложных функций, типа ,  и пр.

Для удобства вывода производных рассматриваемой функции F(x, w) выполним следующую замену:

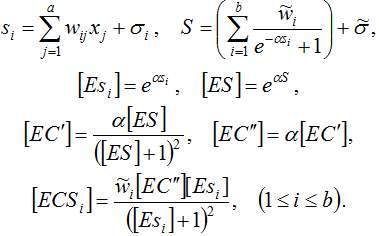
Таким образом, получим:

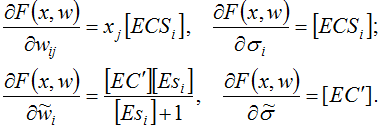
Представленные формулы получены простым взятием производных по известным правилам. Результаты вспомогательных вычислений актуальны в рамках одной строки матрицы Якоби.

Самой «тяжеловесной» функцией в рассматриваемой нейронной сети выступает функция . Заметим, что приведённое выше аналитическое представление для одной строки матрицы Якоби требует 2b+1 вызовов этой функции, в то время как метод разностных производных — 2W(b+1). За счёт этого можно получить значительный прирост производительности, сохранив высокую точность вычислений. Стоит отметить, что комбинирование аналитического подхода с методом Бройдена может оказаться менее эффективным из-за затрат на матричные вычисления и, в силу вносимых неточностей, медленного приближения к точке глобального оптимума.

Очевидно, что аналитический подход к вычислению матрицы Якоби не универсален, так как для каждой новой модели нейронной сети (при изменении количества скрытых слоёв и/или замене активационных функций) потребуется заново выводить формулы. Поэтому, при реализации готовой программной библиотеки для широкого круга задач, рекомендуется включать в неё как метод разностных производных, так и заранее рассчитанные формулы для некоторого множества распространённых моделей. Поскольку каждая строка матрицы J вычисляется независимо от других строк, можно сократить затрачиваемое на вычисления время за счёт использования различных технологий параллельного программирования.

Литература

1. Suri, N. N. R. R. Parallel levenberg-marquardt-based neural network training on linux clusters - a case study / N. N. R. R. Suri, D. Deodhare, P. Nagabhushan // Linux Clusters, ICVGIP 2002, 3rd Indian Conference on Computer Vision, Graphics and Image Processing, Ahmadabad. — 2002.
2. Suratgar, A. A. Modified Levenberg-Marquardt method for neural networks training / A. A. Suratgar, M. B. Tavakoli, A. Hoseinabadi // WEC’05: The Fourth World Enformatika Conference. — 2005.
3. Sousa, C. Neural network learning by the levenberg-marquardt algorithm with bayesian regularization (part 1) [Электронный ресурс] URL: http://crsouza.blogspot.com/2009/11/neural-network-learning-by-levenberg_18.html (дата обращения01.2014).
4. Амосов, А. А. Простейшие формулы численного дифференцирования / А. А. Амосов, Ю. А. Дубинский, Н. В. Копчёнова // Вычислительные методы для инженеров. — Москва: Высшая школа, 1994. — С.364 – 369.
5. Transtrum, M. K. Improvements to the levenberg-marquardt algorithm for nonlinear least-squares minimization / M. K. Transtrum, J. P. Sethna // Journal of Computational Physics. — 2012.
6. Madsen, K. A Secant Version of the L-M Method / K. Madsen, H. B. Nielsen, O. Tingleff // IMM METHODS FOR NON-LINEAR LEAST SQUARES PROBLEMS. — Konigs Lyngby : Technical University of Denmark, 2004. — P. 40 – 45.