MATHEMATICAL MODELING OF PROBLEM THERMOELASTICITY OF A THIN PLATE
Богданова М.В.1, Марочкин С.И.2, Чулюков В.А.3
1Кандидат технических наук, доцент;
2аспирант;
3кандидат физико-математических наук, доцент,
Воронежский государственный педагогический университет
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЗАДАЧИ ТЕРМОУПРУГОСТИ ТОНКОЙ ПЛАСТИНЫ
Аннотация
В работе сформулирована математическая модель задачи о деформации пластины, боковые стенки которой подвергаются тепловому воздействию.
Ключевые слова: моделирование, термоупругость.
Bogdanova M.V.1, Marochkin S.I.2, Chuljukov V.А.3
1PhD in Technical sciences, associate professor;
2postgraduate student;
3PhD in Physics and mathematics, associate professor,
Voronezh State Pedagogical University
MATHEMATICAL MODELING OF PROBLEM THERMOELASTICITY OF A THIN PLATE
Abstract
In work is formulated the mathematical model of a task about deformation the plate which lateral walls are exposed to thermal influence.
Keywords: modeling, thermoelasticity.
Положим, что внутри области с прямоугольным поперечным сечением расположена тонкая пластина, концы которой в течение всего времени эксперимента остаются неподвижными (рис. 1). Выберем декартову систему координат так, чтобы плоскость z = 0 была серединной.
Рассмотрим малые прогибы пластины, ограниченной стенками параллелепипеда. В течение времени t боковые стенки области испытывают тепловое воздействие, прямо пропорциональное времени t. В начальный момент времени пластина неподвижна. Температурное поле внутри области известно. Верхняя и нижняя стенки области теплоизолированы. Требуется рассчитать смещение пластины от положения равновесия в результате теплового воздействия.
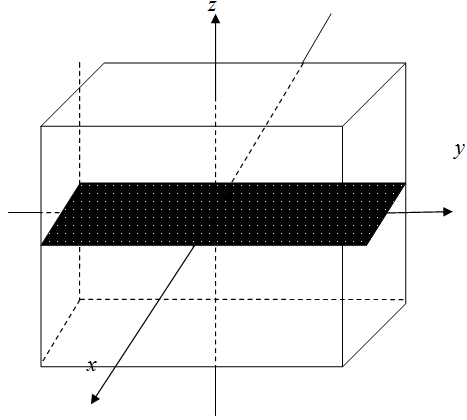
Рис.1 – Модель рассматриваемой установки
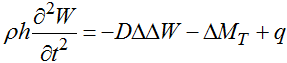 , (1)
В качестве основного уравнения для стационарных прогибов пластины постоянной толщины выступает уравнение Софи Жермен [1, 2]:
, (1)
В качестве основного уравнения для стационарных прогибов пластины постоянной толщины выступает уравнение Софи Жермен [1, 2]:
где D – цилиндрическая жесткость, q – нагрузка на единицу площади пластины, а MT – изгибающий момент, обусловленный температурными воздействиями.
Цилиндрическая жесткость пластины, отражающая упругие и геометрические характеристики пластины, определяется по следующей формуле:
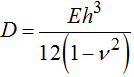 , где
, где ![]() – модуль Юнга, ν – коэффициент Пуассона.
– модуль Юнга, ν – коэффициент Пуассона.
Для MT имеем следующее представление:
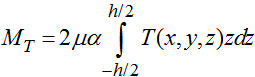 , (2)
, (2)
где α – коэффициент линейного расширения, 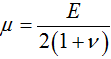 – постоянная Ламе. При этом температурное поле определяется из решения соответствующего уравнения теплопроводности:
– постоянная Ламе. При этом температурное поле определяется из решения соответствующего уравнения теплопроводности:
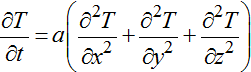 , (3)
, (3)
где a – коэффициент температуропроводности.
Температурное поле в начальный момент времени равно нулю:
![]() (4)
(4)
Температурные поля на границах области прямо пропорциональны времени t:
![]() (5)
(5)
Верхняя и нижняя стенки области теплоизолированы:
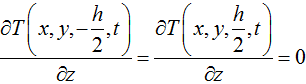 (6)
(6)
В начальный момент времени смещение и скорость смещения пластины равны нулю:
![]() (7)
(7)
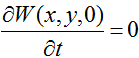 (8)
(8)
На внешней границе Г пластины имеют место следующие условия жесткого закрепления:
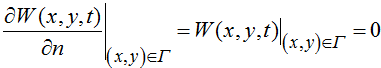 (9)
(9)
Таким образом, система уравнений (1) – (9) есть математическая формулировка поставленной задачи и представляет собой математическую модель исследуемого процесса.
Литература
- Germain S. Recherches sur la theorie des surfaces elastiques. – Paris: 1821. – 96 p.
- Germain S. Remarques sur la nature, les bornes et l’etendue de la question des surfaces elastiques, et equation generale des cer surfaces. – Paris: 1826. – 21 p.
