LABORATORY SIMULATION KIND OF THE STRESS STATE ON THE SAMPLE PRISMATIC
Зеньков Е.В.
Магистрант,
Национальный исследовательский Иркутский государственный технический университет
ЛАБОРАТОРНОЕ МОДЕЛИРОВАНИЕ ВИДА НАПРЯЖЕННОГО СОСТОЯНИЯ НА ОБРАЗЦАХ ПРИЗМАТИЧЕСКОГО ТИПА
Аннотация
В статье предлагается подход к моделированию в лабораторных условиях прочностных характеристик конструктивных узлов, при работе которых в зоне концентрации напряжений реализуется двухосное напряженное состояние (НС). Моделирование требуемого соотношения главных напряжений осуществляется с помощью специальных лабораторных образцов призматического типа, испытываемых на стандартном оборудовании с одним силовым приводом.
Ключевые слова: двухосное напряженное состояние, призматический образец, вид напряженного состояния.
Zenkov E.V.
Under graduate,
National Research Irkutsk State Technical University
LABORATORY SIMULATION KIND OF THE STRESS STATE ON THE SAMPLE PRISMATIC
Abstract
The paper proposes an approach to modeling in laboratory conditions the strength characteristics of structural assemblies, in which the work in the area of stress concentration realized biaxial stress state. Modeling desired ratio of the principal stresses is done using special laboratory samples prismatic type tested on standard equipment with a single actuator.
Keywords: biaxial stress state, prismatic specimen, kind of stress state.
Выполнение требований конструкционной прочности узлов и элементов машин может быть обеспечено при условии наличия достоверных сведений об прочностных характеристиках натурных деталей. Известные методы моделирования характеристик разрушения различных конструкций на лабораторных образцах основаны на статистических (эмпирических) теориях подобия [1]. Существующие методы моделирования учитывают то, что материал изделий в процессе эксплуатации находится в условиях сложного НС недостаточно полно. Например, для таких высоконагруженных конструктивных узлов, как цельнокатаное колесо железнодорожного вагона, внутренние кромки патрубковых зон сосудов высокого давления, диски компрессоров и т.д., в зоне максимального уровня напряжений вид НС отличается особым соотношением компонент главных напряжений. В этом случае предельное состояние материала (предел прочности) конструкции будет зависеть от вида напряженного состояния.
В качестве характеристики вида НС удобно использовать коэффициент вида НС, введенный Смирновым-Аляевым [1]
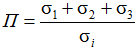 , (1)
, (1)
где σ1, σ2, σ3 – главные напряжения, возникающие в точке наблюдения; σi – эквивалентное напряжение, определяемое формулой:
![]() , (2)
, (2)
Величина П является инвариантной характеристикой вида НС – её большим значениям соответствует (по терминологии Г.А. Смирнова-Аляева) более жёсткий вид НДС, а её меньшим значениям – более мягкий вид НДС. Помимо физической инвариантности, особенностью и, одновременно, преимуществом критерия П, является его зависимость от всех трех главных напряжений в очаге возможного разрушения.
В настоящее время условия прочности при сложном (в частности, при двухосном) НС, реализуемого в конструкциях, определяются уравнениями предельного состояния [1], приведенные к соответствующим гипотезам прочности (Сен-Венана, Мизеса-Хубера-Генки, Мора, Кулона и т.д.). Таким образом, оценка прочности исследуемой конструкции осуществляется путем перехода от сложного НС, реализуемое в зоне конструкции, к простому одноосному, равноопасному ему, используя наиболее подходящий для данного случая критерий предельного состояния (гипотезу прочности). Это значение критерия оценивается из испытаний стандартных образцов на растяжение, сжатие, изгиб или кручение на стандартных испытательных машинах с одним силовым приводом. Проблема же заключается в том, что указанные критерии прочности не чувствительны к виду НС, поэтому получить адекватную картину реального деформирования материала конструкции в условиях стандартных испытаний известных образцов не представляется возможным, что существенно снижает точность проводимых расчетных оценок надежности исследуемых конструкций.
Одной из проблем, возникающих в лабораторных условиях при экспериментальном исследовании характеристик разрушения материала при различных видах НС, является трудность создания в соответствующих лабораторных образцах требуемого соотношения главных напряжений, реализуемых в элементах конструкций
0<П<1 и 1<П<2 (3)
Следует отметить, что при стандартных видах испытаний одноосных образцов в их рабочей зоне, как правило, воспроизводится значение близкое к П=1 (растяжение) и П= –1 (сжатие). При кручении в рабочей зоне стандартного образца первое σ1 и третье σ3 главные напряжения равны по величине и противоположны по знаку, таким образом, получаемое значение П=0.
Для моделирования практически значимого диапазона (3) в настоящее время применение получили испытательные системы с несколькими силовыми независимыми приводами, которые позволяют каждое из главных напряжений в образце создавать независимо (MTS, Instron). Также распространение получило использование нестандартной оснастки, в которой внешнее одноосное усилие распределяется с помощью системы взаимосвязанных рычагов, передающих его на нестандартный образец. В указанных случаях применяются лабораторные образцы трубчатой, крестообразной или прямоугольной формы [2]. Однако, применение сложного испытательного оборудования и нестандартной оснастки значительно усложняют и удорожают процесс соответствующих испытаний, а также вносят систематическую погрешность, связанной с учётом влияния податливости в сочленениях элементов механизмов.
Существенно упростить и снизить стоимость процесса соответствующих испытаний предлагается с помощью призматических образцов. На рисунке 1 представлен вид предлагаемого образца.

Рис. 1 - Призматический образец (а) и его позиционирование в приспособлении (б) при проведении испытаний: 1–образец, 2–боковой выступ со скосами, 3–боковая опора, 4–концевая опора, 5–толкатель
Упрощение процесса испытания с использованием призматического образца достигается заменой одного из силовых воздействий испытательной машины или звена рычажного механизма, позволяющее получать одно из главных напряжений в образце, на контактную силу реакции, реализуемой за счет скольжения упругих элементов L–образной формы по наклонной опорной поверхности приспособления (см. рис. 1, б). Реализованный таким образом научный подход к решению отмеченной проблемы на стадии теоретических и экспериментальных исследований изложен в работе [3]. Особенностью образца является наличие упругих элементов, выполненных в виде боковых выступов L–образной формы, на концах которых располагаются скосы. Существенным преимуществом призматического образца перед известными лабораторными аналогами является проведение механических испытаний на стандартном оборудовании с одним силовым приводом, непосредственно воздействуя на него.
Положительным аспектом предлагаемого призматического образца является чувствительность его геометрических характеристик к изменению параметра вида НС в его рабочей зоне. При варьировании значений указанных характеристик (высоты боковых выступов, радиусов галтелей) появляется возможность создания управляемой схемы НС. Как показали вычислительные эксперименты (см. рис. 2), выполненные в комплексе MSC.Nastran, значение коэффициента П удовлетворяет практически значимому диапазону (3).
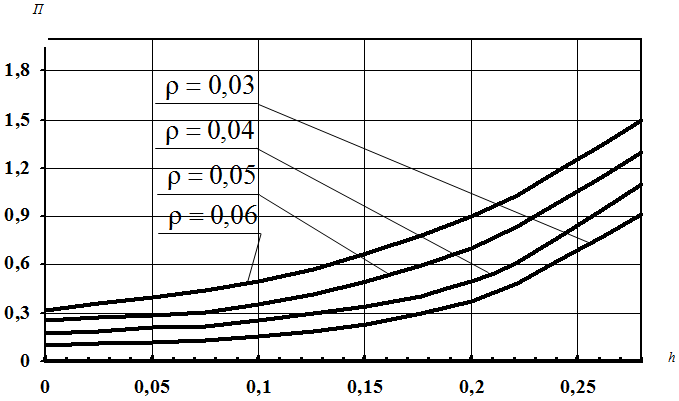
Рис. 2 - Зависимость коэффициента П от высоты вертикальной части L-образного выступа и радиуса галтельного перехода
На рис. 2 введены следующие обозначения: h – относительная высота L-образного выступа (4); ρ – относительный радиус галтельного перехода. В численном эксперименте углы скосов принимались равными 15 градусов. Результаты численного деформирования образца, представленные на рис. 2, справедливы для диапазона изменения геометрических параметров образца
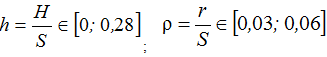 (4)
(4)
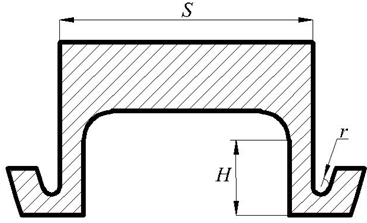
Рис. 3 – Конструктивная схема призматического образца
Зная зависимости изменения коэффициентов П в рабочей зоне образца имеется возможность выбора интересующего конструктивного варианта экспериментального образца для последующего изучения влияния вида НС на предельное состояние материала (предел прочности, предел текучести). Далее, соответственно возможно выполнять расчетную оценку надежности исследуемой конструкции с учетом уточненных данных эксперимента.
Литература
- Когаев В.П., Махутов Н.А., Гусенков А.П. Расчеты деталей машин и конструкций на прочность и долговечность: Справочник. – М.: «Машиностроение». – 1985. – 224 с.
- Вансович К.А., Ядров В.И. Усталостные испытания стальных крестообразных образцов с поверхностной трещиной при двухосном нагружении. // Омский научный вестник №3 (113), 2012. – с. 117–121.
- Зеньков Е.В, Цвик Л.Б. Расчетно-экспериментальная оценка напряженно-деформированного состояния лабораторного образца с галтельным переходом // Вестник ИрГТУ. 2013. №9(80). С. 70 – 78.
