GROUP OF THE ENTERPRISES FOR INDICATORS OF THEIR WORK
Ткаченко В.Я.1, Кузнецов С.М.2, Холомеева Н.В.3, Ольховиков С.Э.4, Колтунова А.А.5
1Доктор экономических наук, профессор;
2Кандидат технических наук, доцент;
3Кандидат экономических наук, доцент;
4Аспирант, старший преподаватель;
5Аспирант, старший преподаватель,
Сибирский государственный университет путей сообщения
ГРУППИРОВКА ПРЕДПРИЯТИЙ ПО ПОКАЗАТЕЛЯМ ИХ РАБОТЫ
Аннотация
Совершенствование анализа хозяйственной деятельности различных производственных образований (предприятий, подразделений, бригад, технологических комплексов и др.) на основе данных статистической отчетности требует разбивки предприятий на группы по показателям их работы.
Ключевые слова: экономический анализ, экономико-статистическое моделирование, железнодорожный транспорт.
Tkachenko V.Ya.1, Kuznetsov S. M.2, Holomeeva N.V.3, Olkhovikov S.E.4, Koltunova A.A.5
1Doctor of Economics, professor;
2PhD in Engineering, docent;
3PhD in Engineering, docent;
4Postgraduate stuent, Senior Lecturer;
5Senior Lecturer Koltunova,
Sibirian Transport University
GROUP OF THE ENTERPRISES FOR INDICATORS OF THEIR WORK
Abstract
Improvement of the analysis of economic activity of various production educations (the enterprises, divisions, crews, technological complexes, etc.) on the basis of data of the statistical reporting demands breakdown of the enterprises on groups on indicators of their work.
Keywords: economic analysis, economical and statistical modeling, railway transport.
Введение
Проведенный в [1] анализ тесноты и характера парных связей между показателями работы производственных предприятий показал, что следующим этапом исследования является разбивка предприятий на группы по показателям их работы. Для этой цели авторами создан алгоритм группировки предприятий (объектов) по данным статистических показателей работы последних [2, 3].
Назначение алгоритма
Алгоритм предназначен для группировки объектов выборки в группы и вычисления статистических характеристик каждой группы и выборки в целом.
Содержательная постановка задачи
Имеется совокупность NO объектов ![]() . Функционирование каждого объекта описывается рядом количественных признаков
. Функционирование каждого объекта описывается рядом количественных признаков ![]() . Один из этих признаков
. Один из этих признаков ![]() является зависимым от остальных
является зависимым от остальных ![]() .
.
Форма зависимости известна. Необходимо определить теоретические значения зависимого признака (Y*) для каждого объекта выборки и сгруппировать по нему объекты в группы. Границы групп (по выравненному Y*) заданы. Для каждой группы и выборки в целом определить статистические характеристики.
Алгоритм решения
Решение осуществляется на основе исходной матрицы данных X(NO, NP) по следующей схеме:
а) среди признаков, характеризующих объекты выборки, устанавливается зависимый (Y);
б) задается вид уравнения многофакторной регрессии;
в) задаются число групп и границы каждой по теоретическому значению зависимого признака Y;
г) по заданному уравнению регрессии и фактическим значениям ![]() определяются теоретические значения зависимого признака (Y*) для каждого объекта выборки;
определяются теоретические значения зависимого признака (Y*) для каждого объекта выборки;
д) по выравненному Y * объекты группируются;
е) для каждой группы устанавливаются номера объектов, вошедших в группу, фактическое и выравненное значение зависимого признака, отклонение выравненного значения от фактического, среднемодульная ошибка аппроксимации зависимого признака;
ж) для выборки в целом определяются среднее значение каждого признака, среднее значение зависимого признака, среднемодульная ошибка аппроксимации зависимого признака.
Описание алгоритма.
Пусть значение ![]() характеризует i-й объект выборки
характеризует i-й объект выборки ![]() . Форма зависимости задана уравнением:
. Форма зависимости задана уравнением:
![]() , (1)
, (1)
где Y* - теоретическое значение зависимого признака;
Xj - фактическое значение независимой переменной, j = 1,…, NP;
![]() - коэффициенты регрессии.
- коэффициенты регрессии.
Задано число групп (KG) и нижняя граница B (KG) каждой группы по выравненному значению зависимого признака (Y*).
Определить вектор ![]() , среднее значение зависимого признака
, среднее значение зависимого признака ![]() , среднемодульную ошибку аппроксимации зависимого признака
, среднемодульную ошибку аппроксимации зависимого признака ![]() , среднее значение независимого признака
, среднее значение независимого признака ![]() для выборки в целом. Сгруппировать объекты в группы, определить номера объектов, вошедших в группу, среднемодульную ошибку аппроксимации зависимого признака в группе. Вектор
для выборки в целом. Сгруппировать объекты в группы, определить номера объектов, вошедших в группу, среднемодульную ошибку аппроксимации зависимого признака в группе. Вектор ![]() определяется по формуле.
определяется по формуле.
Среднее значение зависимого признака ![]() определяется по формуле:
определяется по формуле:
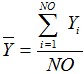 , (2)
, (2)
где NO - число объектов выборки;
Yi - фактическое значение зависимого признака для i-го объекта.
Среднемодульная ошибка аппроксимации зависимого признака ![]() определяется по формуле
определяется по формуле
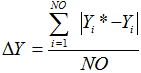 , (3)
, (3)
где ![]() - теоретическое значение зависимого признака для i-го объекта.
- теоретическое значение зависимого признака для i-го объекта.
Среднее значение независимого признака ![]() определяется по формуле
определяется по формуле
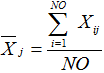 , (4)
, (4)
где ![]() - фактическое значение j-го признака для i-го объекта.
- фактическое значение j-го признака для i-го объекта.
Пусть ![]() - нижняя граница K-ой группы объектов по выравненному значению Y*,
- нижняя граница K-ой группы объектов по выравненному значению Y*, ![]() - нижняя граница следующей по порядку
- нижняя граница следующей по порядку ![]() -ой группы. Тогда в группу K войдут те объекты, для которых
-ой группы. Тогда в группу K войдут те объекты, для которых ![]() .
.
Среднемодульная ошибка аппроксимации зависимого признака Y в K-й группе определяется по формуле
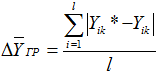 , (5)
, (5)
где l - число объектов, вошедших в K -ю группу;
![]() - теоретическое значение зависимого признака для объекта i в группе K.
- теоретическое значение зависимого признака для объекта i в группе K.
Выводы. С помощью экономико-статистического моделирования разработан способ группировки производственных предприятий по показателям их работы [4]. Способ позволяет более точно планировать деятельность групп предприятий на конкретный промежуток времени (месяц, квартал, год и т.д.). Данный способ является универсальный [5], его можно применять при анализе работы бригад [6], комплексов машин [7], парков [8] и систем [9].
Литература
- Ткаченко В.Я. Анализ тесноты и характера парных связей между показателями работы производственных предприятий / В.Я. Ткаченко, С.М. Кузнецов, Н.В. Холомеева // Экономика ж. д. - 2013. - № 6. - С. 38 - 43.
- Кузнецов С.М. Обработка результатов натурных испытаний при техническом и тарифном нормировании / С.М. Кузнецов, К.С. Кузнецова // Экономика железных дорог, 2010. №7. – С. 88–99.
- Кузнецов С.М. Совершенствование обработки результатов натурных испытаний при техническом и тарифном нормировании / С.М. Кузнецов // Экономика ж. д. - 2013. -№ 7. -С. 90 - 97.
- Котюков В.И., Ткаченко В.Я., Кузнецов С.М. Свидетельство об отраслевой регистрации разработки № 3057 «Программный комплект «КОМПАС»» от 19.12.2003 г.
- Кузнецов С.М. Системотехника ресурсосберегающей технологии строительства зданий и сооружений / С.М. Кузнецов // Изв. вузов. Строительство. -2005. -№ 3. -С. 110 - 117.
- Кузнецов С.М. Подбор состава строительных бригад / С.М. Кузнецов // Экономика ж. д. -2005. -№ 9. -С. 73 - 77.
- Исаков А.Л. Оптимизация работы комплекса машин при строительстве объектов / А.Л. Исаков, К.С. Кузнецова, С.М. Кузнецов// Изв. вузов. Строительство. -2012. -№ 1. -С. 52 - 57.
- Кузнецова К.С. Формирование ресурсосберегающего парка машин / К.С. Кузнецова, С.М. Кузнецов // Путь и путевое хозяйство. -2006. – № 8. -С. 11 - 12.
- Лизунов Е.В. Организационно-технологическая надёжность гидротранспортных систем / Е.В. Лизунов, В.А. Седов, С.М. Кузнецов // Строительные и дорожные машины. -2005. -№ 5. -С. 19 - 21.
