ADDITIVE AND MULTIPLICATIVE MODEL OF ASSESSMENT FOR INNOVATION
Минакова Т. Е. 1, Минаков В. Ф. 2
1Кандидат технических наук, доцент,
Национальный минерально-сырьевой университет «Горный»,
2доктор технических наук, профессор,
Санкт-Петербургский государственный экономический университет
АДДИТИВНО-МУЛЬТИПЛИКАТИВНАЯ МОДЕЛЬ ОЦЕНКИ ИННОВАЦИЙ
Аннотация
Разработана математическая аддитивно-мультипликативная модель оценки инновационных проектов. Отличается учетом как достоинств проектов, так и допустимости по дискретным показателям. Предназначена для отбора проектов для инвестирования.
Ключевые слова: инновационный проект, оценка, модель.
Minakova T.E., Minakov V.F.
1PhD of technical science, associate professor,
National Mineral Resources University,
2Doctor of technical science, professor,
St. Petersburg State University of economics
ADDITIVE AND MULTIPLICATIVE MODEL OF ASSESSMENT FOR INNOVATION
Abstract
The mathematical additive and multiplicative model of an assessment of innovative projects is developed. Differs the account as advantages of projects, and an admissibility on discrete indicators. It is intended for selection of projects for investment.
Keywords: innovative project, assessment, model.
Практика управления современными предприятиями требует оценки и принятия решений об использовании инноваций [1, 2], изменяющих способы производства, продукцию, ее качество [3-6]. В наибольшей степени это относится к стратегиям развития информационных ресурсов [7].
Анализ используемых в настоящее время методов, моделей, метрик и критериев оценки инновационных проектов [8, 9] позволяет установить, что очень часто допускается необоснованное арифметическое суммирование показателей оценки: аналоговых показателей, например, эффективности, и показателей соответствия проекта его инновационному назначению – дискретных показателей в виде метрики:
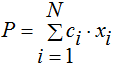 ,
,
где ![]() – метрика инновационного проекта;
– метрика инновационного проекта;
![]() – вес показателя.
– вес показателя.
Такой подход не позволяет исключить проекты, аналогичные фильтрам Петрика, при попытках его внедрения для очистки радиоактивной воды и последующего использования ее в качестве питьевой. Модель, следовательно, должна даже при наличии большого числа достоинств проекта (отражаемых аналоговыми показателями), исключать возможность его реализации, то есть дискретно нивелировать оценку [10].
В связи с этим предлагается разделение показателей инновационных проектов на два ключевых класса:
– аналоговые (непрерывные) показатели – это класс показателей инновационного проекта позволяющий оценить предпочтительные свойства проекта на каждом из этапов его жизненного цикла, позволяющие получить показатель проекта как сумму его нормированных характеристик, отражающих достоинства;
– дискретные (прерывистые) показатели, независимые от аналогового результата оценки инновационных проектов, например, принимающие нулевое или единичное значение, позволяющие отклонять проекты в случае невозможности их реализации по критерию недопустимости таких проектов для использования.
Если метрики предпочтительных характеристик проектов могут быть отражены аддитивно в интегральном показателе, то возможность или невозможность принятия проекта должна учитываться мультипликативно, отображая тем самым логическую операцию «И». Смысл такой операции и характерен для дискретных булевых величин: отбор инновационного проекта и принятие к реализации предполагает и наличие достоинств проекта, сумма которых учитывается аддитивно, и одновременно требуется реализуемость и допустимость реализации проекта по критически важным показателям.
Следовательно, формализованная математическая интегральная оценка инновационного проекта должна быть выражена аддитивно-мультипликативной моделью:
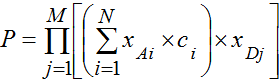
где Р – интегральная оценка (рейтинговая) инновационного проекта;
![]() – аналоговый показатель;
– аналоговый показатель;
![]() – критически важные дискретные показатели инновационного проекта,
– критически важные дискретные показатели инновационного проекта,
j – номер дискретного показателя.
Заключение
Аддитивно-мультипликативная модель оценки инноваций позволяет, во-первых, учесть все преимущества инновационного проекта, во-вторых, исключает его применение в случае несоответствия критическим показателям (законность, безопасность для жизни и здоровья потребителей).
Литература
- Аванесов Г. М. Развитие систем поддержки управленческих решений промышленного предприятия // Научно-технические ведомости СПбГПУ. Экономические науки. – 2009. – № 6. – С. 99-104.
- Аванесов Г. М. Тенденции интеграционных бизнес-процессов в промышленности: теория, методология, механизмы реализации. – СПб.: Изд-во Санкт-Петербургского государственного университета экономики и финансов. – 2006. – 111 с.
- Минакова Т. Е. Оценка потенциала энергосбережения в общественном воспроизводстве // Экономика, статистика и информатика. Вестник УМО. – 2013. – № 3. – С. 127-129.
- Минакова Т. Е., Минаков В. Ф. Синергия энергосбережения при высокой добавленной стоимости продукции // Современные проблемы науки и образования. – 2013. – № 4. – С. 26.
- Минаков В. Ф., Минакова Т. Е. Математическая модель кумулятивного эффекта энергосбережения // Известия высших учебных заведений. Электромеханика. – 2013. – № 1. – С. 197–199.
- Минаков В. Ф., Минакова Т. Е. Способ быстродействующей защиты электродвигателей от несостоявшихся пусков // Альманах современной науки и образования. Тамбов: Грамота. – 2013. – № 9 (76). – С. 113–115.
- Минаков В. Ф., Минакова Т. Е. Модернизация региональных информационных ресурсов в облачные платформы и сервисы // Международный научно-исследовательский журнал = Research Journal of International Studies. – 2013. – № 10 (17). – С. 56-57.
- Минаков В. Ф., Минакова Т. Е., Галстян А. Ш., Шиянова А. А. Обобщенная экономико-математическая модель распространения и замещения инноваций // Экономический анализ: теория и практика. – 2012. – № 47 (302). – С. 49-54.
- Минаков В. Ф., Минакова Т. Е. Модель восприятия инноваций с учетом убывающей предельной производительности // Современные аспекты экономики. – 2013. – № 9 (193). – С. 18-22.
- Минакова Т. Е., Минаков В. Ф. Классификация показателей привлекательности инноваций // Современные аспекты экономики. – 2013. – № 10 (194). – С. 48-53.
