A STUDY OF ANGULAR DISTRIBUTIONS OF CRYSTALLITES IN POLYCRYSTALS WITH HCP-STRUCTURE

ИЗУЧЕНИЕ УГЛОВЫХ РАСПРЕДЕЛЕНИЙ КРИСТАЛЛИТОВ В ПОЛИКРИСТАЛЛАХ С ГПУ-СТРУКТУРОЙ

Научная статья

Степаненко А.В.*

ORCID: 0000-0001-7804-8918,

Уральский федеральный университет имени первого Президента России Б.Н. Ельцина, Екатеринбург, Россия

* Корреспондирующий автор (avstep[at]mail.ru)

Аннотация

Кристаллографическая текстура оказывает определяет анизотропию физических свойств металлов и сплавов. На практике распространен метод расчета анизотропии физических свойств поликристаллов, основанный на использовании функции распределения ориентировок кристаллитов. Основной математический метод получения функции распределения ориентировок кристаллитов связан с разложением функции распределения в ряд по обобщенным шаровым функциям и с разложением полюсных фигур в ряд по сферическим функциям (метод Роу-Бунге). Однако, функция распределения по ориентировкам кристаллитов принципиально не может быть однозначно определена по полюсным фигурам. Предложен простой способ получения  функции углового распределения кристаллитов по ориентировкам в поликристаллах, которые имеют текстуру базисного типа. Базисная текстура приводит к изотропии свойств в плоскости прокатки металлов с ГПУ-структурой. Поэтому представляет интерес угловое распределение кристаллитов  относительно нормали к плоскости прокатки (распределение по полярному углу θ). Функция распределения кристаллитов  может быть использована для расчетов анизотропных физических свойств поликристалла.

Ключевые слова: поликристаллы, текстура, анизотропия, структура, деформация, редкоземельные металлы, рентгеновский анализ, дифракция.

A STUDY OF ANGULAR DISTRIBUTIONS OF CRYSTALLITES IN POLYCRYSTALS WITH HCP-STRUCTURE

Research article

Stepanenko A.V.*

ORCID: 0000-0001-7804-8918,

Ural Federal University, Ekaterinburg, Russia

* Corresponding author (avstep[at]mail.ru)

Abstract

The crystallographic texture determines the anisotropy of the physical properties of metals and alloys. In practice, a widespread method for calculating the anisotropy of the physical properties of polycrystals, based on the use of the distribution function of crystallite orientations. The main mathematical method for obtaining the distribution function of crystallite orientations is associated with the expansion of the distribution function in a series in generalized spherical functions and with the expansion of pole figures in a series in spherical functions (the Roe-Bunge method). However, the distribution function by crystallite orientations, in principle, cannot be unambiguously determined from the pole figures. A simple method is proposed for obtaining  of the angular distribution function of crystallites over orientations in polycrystals with a basic texture. The basic texture leads to isotropy of properties in the rolling plane of metals with an hcp structure. Therefore, the angular distribution of crystallites  relative to the normal to the rolling plane (distribution over the polar angle θ) is of interest. The crystallite distribution function  can be used to calculate the anisotropic physical properties of a polycrystal.

Keywords: polycrystals, texture, anisotropy, structure, deformation, rare-earth metals, X-ray analysis, diffraction.

Introduction

The crystallographic texture has a decisive effect on the level of anisotropy of physical and mechanical properties (magnetic susceptibility, electrical resistance, etc.) of polycrystalline metals and alloys [1], [2]. Taking into account the anisotropy of physical and mechanical properties makes it possible to reduce the metal consumption and hang the level of service properties of industrial materials [3].

The texture is capable of forming with any thermomechanical methods of processing materials, while its type and degree of intensity significantly depend on the purity of the samples used, depends on the previous state of the material [4]. X-ray texture studies are the most common methods used in factory laboratories. Such methods are more accessible than neutron diffraction, and more informative than ultrasonic and metallographic methods [5], [6].

In practice, various methods are used for calculating the properties of metals based on texture data [3], [7], [10]. There are methods for calculating the anisotropic properties of polycrystalline materials based on the determination of experimental texture macro-parameters (calculation of the orientation factors ∆_i [3] ,[7]). Such methods make it possible to evaluate the anisotropy of the physical and mechanical properties of metal samples, but do not provide accurate information on the distribution of crystallite orientations and their relationship with the anisotropy of the physical properties of the material.

The calculation of the anisotropic properties of polycrystals can be performed on the basis of the experimental distribution function of crystallite orientations (ODF). This method was proposed by Viglin [1] and then developed by Roe [12] and Bunge [13], [14]. In the Roe-Bunge method, it was proposed to calculate the distribution function of crystallite orientations based on the expansion of the distribution function in a series in generalized spherical functions and on the expansion of pole figures in a series in spherical functions.

The distribution function of crystallite orientations cannot be obtained as a result of direct measurement [15]. Only pole figures can be measured. Therefore, the main task of quantitative texture analysis is the problem of calculating the distribution function of crystallites by orientation based on a finite number of experimental pole figures. Methods and materials

This paper presents a method for determining the angular distribution of crystallites in polycrystals, based on the use of experimental data of X-ray texture analysis. The texture of the metal sample was investigated on a DRON-0.5 X-ray diffractometer by the method of reverse pole figures [6]. Figure 1 shows the positions of the crystallographic orientations on the reverse pole figure for hcp metals.

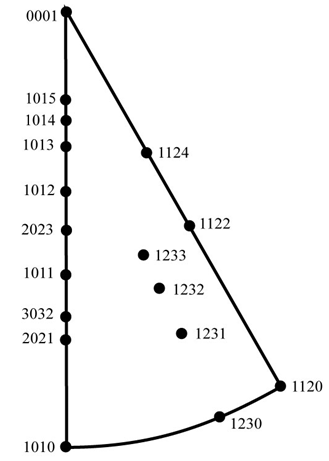
Fig. 1 – Pole distribution on a reverse pole figure

  The pole densities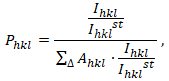  on the stereographic triangle were determined using the Morris method: where  – integrated intensity of X-ray reflection for the  orientation of crystallites of the sample under study,  – integrated intensity of X-ray reflection for the  orientation of the crystallites of the standard sample,  – Morris coefficients. For the majority of metals with an hcp structure, 17 crystallographic orientations are studied to construct reverse pole figures. The calculation of crystallite fractions was carried out for the case of sharp textures, taking into account the Morris coefficients and the repeatability factor:

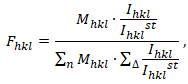
where  – fraction of crystallites that corresponds to the orientation ,

 – repeatability factor for orientation ,

 n – number of investigated crystallographic orientations.

In metal samples with an hcp crystal lattice, after plastic deformation by rolling, a basic type crystallographic texture is often formed [16–18]. In this case, the rolling plane is the isotropy plane of tensor physical quantities of the second rank [3]. Therefore, of interest is the angular distribution of crystallites relative to the normal to the rolling plane (distribution over the polar angle θ). Determination of this distribution can be considered the first stage of restoration of a three-dimensional ODF.

A polar angle θ corresponds to each crystallographic orientation. Therefore, not only the distribution of the pole density  over the crystallographic orientations is of interest, but also the angular distribution of the crystallite fractions F (θ) over the polar angle θ.

On the basis of the inverse pole figures, one can obtain the angular distribution of the crystallite fractions F (θ) over the polar angle θ. The experimental dependence F (θ) can be used to calculate the crystallite distribution function  over the polar angle θ. This calculation can be done using polynomial regression.

The crystallite distribution function  can be used to calculate the anisotropic physical properties of a polycrystal [3]:

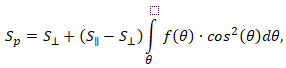where  – the single-crystal parameters of the hcp metal.

High-purity dysprosium (polycrystalline material with a hexagonal crystal structure:  was selected as samples for the study. To obtain a crystallographic texture, the sample under study was deformed by cold rolling without using recrystallization annealing.

Results and their discussion

After plastic deformation by cold rolling with a degree of deformation ε = 50%, a sharp crystallographic texture of the basic type  was formed in a sample of polycrystalline Dy (see Fig. 2).

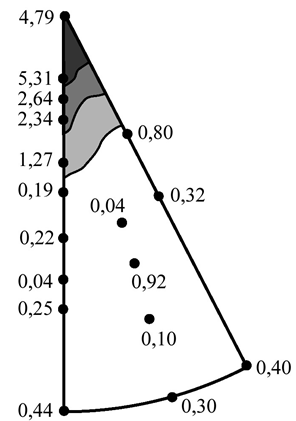
Fig. 2 – Reverse pole figure of a deformed polycrystal

 

On the reverse pole figure of dysprosium, the basic (0001) and pyramidal  crystallite orientations are distinguished, which have a small scattering of the pole density. This feature of the rolling texture of the sample under study indicates that the main mechanism of deformation in the material is slip along the basic system . The slipping of a dislocation along the prismatic system  for the sample under study is a secondary deformation mechanism.

A similar deformation texture is observed in other metals with an hcp structure [1], [16], [17]. The sharp basic component of the rolling texture in samples of hcp metals leads to isotropy of physical and mechanical properties in the rolling plane and anisotropy of physical properties in the plane perpendicular to the rolling direction.

Figure 3 shows the obtained distributions of the pole density on the reverse pole figure and the distribution of the fraction of crystallites in the dysprosium sample by orientations. To determine the distribution function of crystallites over the polar angle , polynomial regression was used, which gives local approximations by segments of second-degree polynomials.

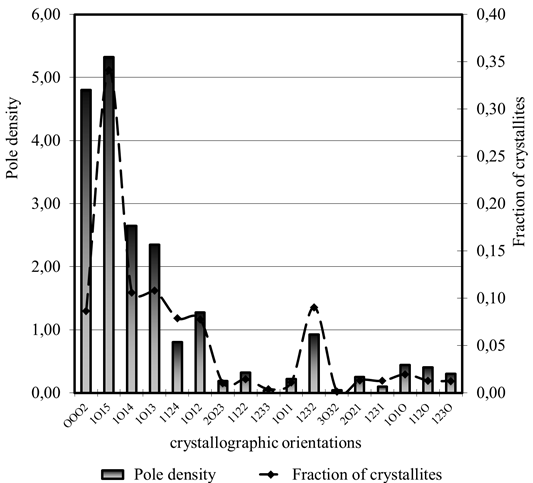
Fig. 3 – Distribution of pole density and fraction of crystallites by crystallographic orientations

 

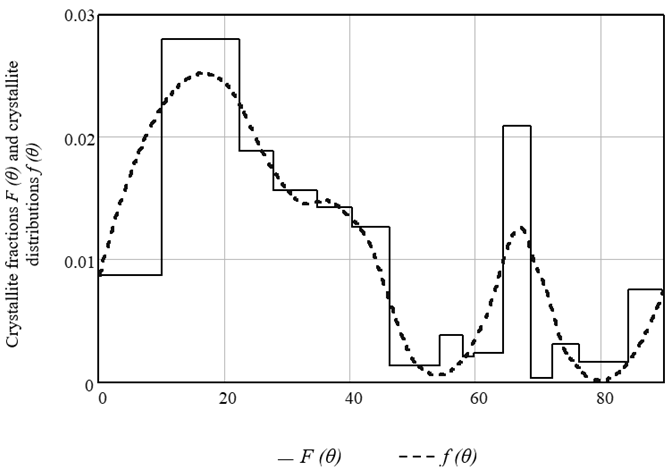
Figure 4 compares the distribution of crystallite fractions over the polar angle θ and the graph of the function  for a metal sample.

The angular distribution functions  obtained on the basis of the inverse pole figure were used to determine the S_p values of the anisotropic physical properties Dy.

Calculations of the magnetic susceptibility χ of a deformed sample Dy show that for the rolling direction χ_rd and for the normal direction to the rolling plane χ_nd, the value of anisotropy , which agrees with the experimental results of determining the magnetic susceptibility of the studied polycrystal.

Fig. 4 – Distribution of crystallite fractions by polar angle θ and graph of the function f(θ) for the sample

Conclusions

The method for calculating the distribution function of crystallite orientations based on the expansion of the distribution function of crystallites by orientations in a series of generalized spherical functions, is mathematically complex, ambiguous, and difficult to use in practice. The proposed method for the experimental study of the distribution of crystallites by orientations simplifies the problem. Using polynomial regression for experimental data allows you to quickly obtain the function , which makes it possible to calculate the anisotropic physical properties of a polycrystal. 

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References

1. Кудрявцев И. П. Текстуры в металлах и сплавах / И. П. Кудрявцев. – М.: Металлургия, 1965. – 292 с.
2. Kocks F. Texture and Anisotropy. Preferred Orientations in Polycrystals and Their Effect on Material Properties / Kocks Fred & Tomé, Carlos & Wenk H-R. – Cambridge University Press, 2000. – 676 p.
3. Адамеску Р.А. Анизотропия физических свойств металлов / Р. А. Адамеску, П. В. Гельд, Е. А. Митюшов. – М. : Металлургия, 1985. – 137 с.
4. Вишняков Я. Д. Теория образования текстур в металлах и сплавах / Я. Д. Вишняков, А. А. Бабарэко, С. А. Владимиров, И. В. Эгиз. – М. : Наука, 1979. – 344 с.
5. Лобанов М. Л. Методы исследования текстур в материалах / М. Л. Лобанов, А. С. Юровских, Н. И. Кардонина, Г. М. Русаков. – Екатеринбург: Изд-во Уральского университета, 2014. – 115 с.
6. Бородкина М. М. Рентгенографический анализ текстуры металлов и сплавов / М. М. Бородкина, Э. Н. Спектор. – М. : Металлургия, 1981. – 271 с.
7. Митюшов Е. А. Формальная схема расчета эффективных упругих свойств текстурированных металлов / Е. А. Митюшов, Н. Ю. Одинцова, С. А. Берестова // Математическое моделирование систем и процессов. – 2003. – №11. – С. 76–80.
8. Яковлев С. С. Анизотропия механических свойств и кристаллографическая текстура гексагональных плотноупакованных металлов / С. С. Яковлев, В. Д. Кухарь // Известия ТулГУ. Технические науки. – 2011. – Вып.1. – С. 41–49.
9. Perlovich Yu. Three laws of substructure anisotropy of textured metal materials, revealed by X-ray method of generalized pole figures / Yu. Perlovich, M. Isaenkova, V. Fesenko // Materials Processing and Texture, Ceramic Transactions. – 2008. – Vol. 200. – P. 539–546.
10. Betsofen S. Ya. Texture and anisotropy in the mechanical properties of titanium alloys caused by the mechanism of plastic deformation / S. Ya. Betsofen, A. A. Ilyin, V. V. Plikhunov, A. D. Plotnikov, A. A. Filatov // Russian Metallurgy (Metally). – 2007. – Vol. 2007. – Iss.5. – P. 387–393.
11. Степаненко А. В. Исследование анизотропии свойств поликристалла на основе текстурных данных / А. В. Степаненко // Заводская лаборатория. Диагностика материалов. – 2019. – Т. 85. – №9. – С. 46–51.
12. Roe R. J. Description of Crystallite Orientation in Polycrystalline Materials / R. J. Roe // Journ. Appl. Phys. – 1965. – V. 36. – №6. – P. 2024–2031.
13. Bunge H. I. Zur Darstelung algemeiner Texturen / H. I. Bunge // Z. Metallkunde. – 1965. – Bd.56. – P. 872–874.
14. Bunge H. I. The basic concepts of texture investigation in polycrystalline materials / H. I. Bunge // Steel Res. – 1991. – Vol. 62. – №12. – P. 530–541.
15. Мatthies S. Study of the ghost phenomena in mathematical texture analysis by means of standard functions / S. Matthies, F. Wagner // Phys. stat. sol. B. – 1981. – Vol. 102. – №2. – P. 591–601.
16. Золоторевский Н. Ю. Фрагментация и текстурообразование при деформации металлических материалов / Н. Ю. Золоторевский, В. В. Рыбин // СПб.: Издательство Политехнического университета, 2014. – 208 с.
17. Степаненко А. В. Определение текстурных параметров поликристаллов с острой однокомпонентной текстурой / А. В. Степаненко // Успехи современной науки и образования. – 2016. – №9. – Т. 4. – С. 149–153.
18. Дзунович Д. А. Методические аспекты количественного текстурного анализа листовых полуфабрикатов из ГПУ-сплавов (Ti, Zr) / Д. А. Дзунович, С. Я. Бецофен, П. В. Панин // Деформация и разрушение материалов. – 2016. – №11. – С. 8–16.

Список литературы на английском языке / References in English

1. Kudryavcev I. P. Tekstury v metallah i splavah [Textures in metals and alloys] / I. P. Kudryavtsev. - M.: Metallurgy, 1965. – 292 p. [in Russian]
2. Kocks F. Texture and Anisotropy. Preferred Orientations in Polycrystals and Their Effect on Material Properties / Kocks Fred & Tomé, Carlos & Wenk H-R. – Cambridge University Press, 2000. – 676 p.
3. Adamesku R.A. Anizotropiya fizicheskih svojstv metallov [Anisotropy of the physical properties of metals] / R. A. Adamesku, P. V. Gel'd, E. A. Mityushov. – M.: Metallurgy, 1985. – 137 p. [in Russian]
4. Vishnyakov YA. D. Teoriya obrazovaniya tekstur v metallah i splavah [The theory of texture formation in metals and alloys] / YA. D. Vishnyakov, A. A. Babareko, S. A. Vladimirov, I. V. Egiz. – M.: Nauka, 1979. – 344 p. [in Russian]
5. Lobanov M. L. Metody issledovaniya tekstur v materialah [Methods for studying textures in materials] / M. L. Lobanov, A. S. YUrovskih, N. I. Kardonina, G. M. Rusakov. – Yekaterinburg: Publishing house of the Ural University, 2014. – 115 p. [in Russian]
6. Borodkina M. M. Rentgenograficheskij analiz tekstury metal-lov i splavov [X-ray analysis of the texture of metals and alloys] / M. M. Borodkina, E. N. Spektor. – M.: Metallurgy, 1981. – 271 p. [in Russian]
7. Mityushov E. A. Formal'naya skhema rascheta effektivnyh uprugih svojstv teksturirovannyh metallov [Formal scheme for calculating the effective elastic properties of textured metals] / E. A. Mityushov, N. YU. Odincova, S. A. Berestova // Matematicheskoe modelirovanie sistem i processov [Mathematical modeling of systems and processes]. – 2003. – No. 11. – 76–80. [in Russian]
8. YAkovlev S.S. Anizotropiya mekhanicheskih svojstv i kristallo-graficheskaya tekstura geksagonal'nyh plotnoupakovannyh metallov [Anisotropy of mechanical properties and crystallographic texture of hexagonal close-packed metals] / S. S. YAkovlev, V. D. Kuhar' // Izvestiya TulGU. Tekhnicheskie nauki [Bulletin of TulSU. Technical science]. – 2011. - Issue 1. - P. 41–49. [in Russian]
9. Perlovich Yu. Three laws of substructure anisotropy of textured metal materials, revealed by X-ray method of generalized pole figures / Yu. Perlovich, M. Isaenkova, V. Fesenko // Materials Processing and Texture, Ceramic Transactions. – 2008. – Vol. 200. – P. 539–546.
10. Betsofen S. Ya. Texture and anisotropy in the mechanical properties of titanium alloys caused by the mechanism of plastic deformation / S. Ya. Betsofen, A. A. Ilyin, V. V. Plikhunov, A. D. Plotnikov, A. A. Filatov // Russian Metallurgy (Metally). – 2007. – Vol. 2007. – Iss.5. – P. 387–393.
11. Stepanenko A. V. Issledovanie anizotropii svojstv polikristalla na osnove teksturnyh dannyh [Investigation of the anisotropy of polycrystal properties based on texture data] / A. V. Stepanenko // Zavodskaya laboratoriya. Diagnostika materialov [Factory laboratory. Diagnostics of materials]. – 2019. - Vol. 85. - No. 9. - P. 46-51. [in Russian]
12. Roe R. J. Description of Crystallite Orientation in Polycrystalline Materials / R. J. Roe // Journ. Appl. Phys. – 1965. – V. 36. – №6. – P. 2024–2031.
13. Bunge H. I. Zur Darstelung algemeiner Texturen / H. I. Bunge // Z. Metallkunde. – 1965. – Bd. 56. – P. 872–874.
14. Bunge H. I. The basic concepts of texture investigation in polycrystalline materials / H. I. Bunge // Steel Res. – 1991. – Vol. 62. – №12. – P. 530–541.
15. Мatthies S. Study of the ghost phenomena in mathematical texture analysis by means of standard functions / S. Matthies, F. Wagner // Phys. stat. sol. B. – 1981. – Vol. 102. – №2. – P. 591–601.
16. Zolotorevskij N. YU. Fragmentaciya i teksturoobrazovanie pri deformacii metallicheskih materialov [Fragmentation and texture formation during deformation of metal materials] / N. YU. Zolotorevskij, V. V. Rybin // Saint Petersburg: Publishing House of the Polytechnic University, 2014. – 208 p. [in Russian]
17. Stepanenko A. V. Opredelenie teksturnyh parametrov polikristallov s ostroj odnokomponentnoj teksturoj [Determination of texture parameters of polycrystals with a sharp one-component texture] / A. V. Stepanenko // Uspekhi sovremennoj nauki i obrazovaniya [Advances in modern science and education]. – 2016. – No. 9. – Vol. 4. – P. 149–153. [in Russian]
18. Dzunovich D. A. Metodicheskie aspekty kolichestvennogo teksturnogo analiza listovyh polufabrikatov iz GPU-splavov (Ti, Zr) [Methodological aspects of quantitative texture analysis of sheet semi-finished products made of hcp alloys (Ti, Zr)] / D. A. Dzunovich, S. YA. Becofen, P. V. Panin // Deformaciya i razrushenie materialov [Deformation and destruction of materials]. – 2016. – No. 11. – P. 8–16. [in Russian]