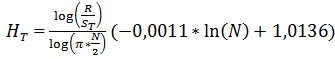ПОКАЗАТЕЛЬ ХЕРСТА КАК МЕРА ФРАКТАЛЬНОЙ СТРУКТУРЫ И ДОЛГОСРОЧНОЙ ПАМЯТИ ФИНАНСОВЫХ РЫНКОВ
Некрасова И.В.
Кандидат экономических наук, доцент, Южный федеральный университет
ПОКАЗАТЕЛЬ ХЕРСТА КАК МЕРА ФРАКТАЛЬНОЙ СТРУКТУРЫ И ДОЛГОСРОЧНОЙ ПАМЯТИ ФИНАНСОВЫХ РЫНКОВ
Аннотация
В данной статье обосновывается практическая значимость Гипотезы фрактального рынка на основе расчета показателя Херста. Основная цель данной статьи заключается в анализе методов прогнозирования будущих цен финансовых активов, основываясь на концепции фрактальной структуры рынка и долговременной памяти рыночных цен.
Ключевые слова: антиперсистентный стохастический процесс, персистентный (инерция) стохастический процесс, долгосрочная память рынка, фрактал, Гипотеза эффективного рынка, Гипотеза фрактального рынка.
Nekrasova I.V.
PhD in economic, docent, South Federal University
THE HURST INDEX AS A MEASURE FOR THE FRACTAL STRUCTURE AND LONG-TERM MEMORY OF FINANCIAL MARKETS
Abstract
The paper overall goal is to analyze methods of forecasting future prices of financial assets, basing on the concept of the fractal market structure and long-term memory of prices.
Keywords: persistent stochastic process, antipersistent stochastic process, long-term memory, fraction, Efficient Market Hypothesis, Fractal Market Hypothesis.
В настоящее время большинство экономистов отрицают возможность использования Efficient Market Hypothesis (EMH) для анализа финансовых рынков, несмотря на то, что классическая финансовая теория базируется на гипотезе эффективного рынка (ЕМН) и предположении о том, что изменения цен на активы имеют нормальное распределение.
В 1960-х и 1970-х годах Юджин Фама выдвинул Efficient Market Hypothesis (EMH) и показал, что если рынок удовлетворяет этой гипотезе, то он является эффективным [1]. Теория Юджина Фамы основывается на традиционных методах финансового анализа, предложенных Луи Башелье [2].
Однако Б. Мандельброт установил факт персистентности рыночных цен (price persistence), т.е. способности некоторой тенденции на рынке существовать дольше, чем процесс, который ее создал. Согласно результатам его анализа финансовые рынки обладают долгосрочной памятью, которая выражается либо в персистентности , либо в антиперсистентности временных рядов цен [3].
При антиперсистентном стохастическом процессе после возрастания переменной обычно происходит ее уменьшение, а после уменьшения - возрастание.
Поэтому Mandelbrot предложил использовать вместо Гипотезы эффективного рынка (Fractal Market Hypothesis) Гипотезу фрактального рынка.
Гипотеза фрактального рынка (FMH, Fractal Market Hypothesis) применительно к финансовым рынкам была развита в работах Э. Петерса (1991, 1994). [4]
Основные положения FMH состоят в следующем.
- Рынок является стабильным, когда он состоит из инвесторов, имеющих различные инвестиционные горизонты. Это обеспечивает высокую ликвидность финансовых рынков.
- Когда инвесторы с длинными инвестиционными горизонтами или прекращают участвовать на рынке, или сами становятся краткосрочными инвесторами, финансовые рынки становятся нестабильными.
- Цены складываются под воздействием информации, получаемой как от технического анализа, так и от фундаментального.
- Ликвидность финансовых рынков не ассоциируется с объемом торгов. Так как самые крупные финансовые кризисы происходили, как правило, на фоне больших объемов торгов.
- Важность информации на финансовых рынках определяется инвестиционным горизонтом инвестора. Поскольку инвесторы с различными инвестиционными горизонтами оценивают информацию по-разному, распространение информации на рынке также будет неравномерным.
- Источником ликвидности на финансовых рынках являются инвесторы с различными инвестиционными горизонтами, различными информационными множествами и, следовательно, с различными представлениями о справедливой цене.
Согласно Гипотезе фрактального рынка финансовые рынки характеризуются различной степенью пластичности, которая может быть определена как способность принимать и сохранять форму. Это означает, что рынки могут значительно меняться, с точки зрения их формы и функций, и что они в состоянии сохранять изменения в форме вновь приобретенных свойств, даже если причины таких изменений перестают существовать.
Пластичность финансового рынка – это двойственная конструкция; она предполагает, как способность изменять, так и способность удерживать (сохранять) форму в течение продолжительного периода времени. Все рынки пластичны, но степень их пластичности может меняться, поэтому изучение взаимосвязи между изменчивостью и стабильностью позволит лучше понять динамику рынка.
Экономическая теория различает структурную и организационную пластичность.
Структурная пластичность относится к способности финансовых рынков двигаться в сторону большей конгруэнтности через повторяющиеся пертурбации.
Организационная пластичность относится к способности системы, нейтрализовать внешние структурные изменения, посредством собственных внутренних структурных изменений.
В экономике и в финансах, в частности, существует два основных направления использования термина пластичности.
Alchian A. и Woodward S. (1988) использовали термин «пластичность активов», чтобы указать на наличие широкого диапазона различных решений, которые может выбрать инвестор. [5]
Strambach (2010) рассматривал пластичность как «институциональную пластичность», в контексте того, что финансовые институты и учреждения могут оказывать как стимулирующее, так и сдерживающее воздействие на финансовые рынки, посредством административных и рыночных инструментов регулирования. [6]
Таким образом, можно определить пять основных аспектов пластичности финансовых рынков: способность принимать, сохранять, передавать, уничтожать форму и изменять функции. Под формой можно понимать структуру различных финансовых активов или финансовых продуктов, которая подстраивается под различные внешние условия. Структура самих финансовых рынков обусловлена структурой финансовых продуктов, которая регулируется финансовыми институтами. Чем многообразнее финансовые продукты, тем более устойчивы финансовые рынки. Разнообразные виды финансовых продуктов образуют фрактальную структуру рынка.
Основным методом изучения фрактальной структуры финансовых рынков является R/S-анализ, или метод нормированного размаха. Он был разработан английским гидрологом Гарольдом Эдвином Хёрстом. [7]
Существует две вариации фрактальной размерности – D и A. Так, фрактальную размерность D (D - это оценка степени изломанности ряда) определяют по следующей формуле 1.
- Mandelbrot в своей работе показал, что фрактальная размерность является обратной величиной от показателя Херста (коэффициент Hurst – H). Например, при H = 0.5 фрактальная размерность равна 2 (1/0.5), а при H = 0.8 фрактальная размерность равна 1.25 (1/0.8).
Таким образом, фрактальную размерность по Mandelbrot, обозначаемую буквой А (А - это размерность пространства вероятностей, т.е. оценка толщины хвостов в функции плотности вероятности) рассчитывают по формуле 2:
Таблица 1 - Значения вариаций фрактальной размерности [1]
Показатель Херста может быть определен на отрезке [0, 1], и рассчитан в следующих пределах:
- если 0 ≤ H < 0,5 – цены являются фракталами, подтверждается справедливость FMH, имеют место «тяжелые хвосты» в распределении переменных, антиперсистентныесерии, т.е. отрицательная корреляцияв изменениицен, розовый шумс частымиизменениями направлениядвиженияцен;
- если Н = 0,5 – цены являются случайными, подтверждается справедливость EMH, движение цен на финансовые активы является примером случайного броуновского движения (Винер процесса), временные ряды, как правило, нормально распределены, отсутствует корреляция в изменении стоимости активов (память), подтверждается наличие белого шума;
- если 0,5 < H ≤ 1 - цены являются фракталами, подтверждается справедливость FMH, имеют место «тяжелые хвосты» в распределении переменных, персистентные серии, т.е. положительная корреляция в изменении цен, присутствует черный шум, свидетельствующий о наличии трендов на рынке;
За точку отсчета Hurst взял формулу из работы Эйнштейна о броуновском движении частиц.
R – расстояние, пройденное броуновской частицей за время Т,
Т – показатель времени.
Согласно этой формуле броуновская частица продвигалась на расстояние, равное квадратному корню времени, затраченному на это продвижение.
Расчет показателя Hurst можно провести по следующей формуле:
H – показатель Hurst;
S – среднеквадратичное отклонение ряда наблюдений x;
R – размах накопленного отклонения Zu;
N – число периодов наблюдений;
a – заданная константа, положительное число. Херст эмпирически рассчитал эту константу для сравнительно краткосрочных временных рядов природных явлений как 0.5.
Однако если в качестве константы использовать число 0,5, то при небольшом количестве наблюдений N показатель Hurst имеет склонность даже на случайных рядах оценивать их как персистентные (обладающие трендами), завышая H. Поэтому для дальнейшего исследования рыночных рядов необходимо использовать константу a= p/2.
Х – среднее арифметическое ряда наблюдений х за N периодов:
Размах накопленного отклонения R является наиболее важным элементом формулы расчета показателя Hurst. В общем виде его вычисляют следующим способом:
Zu - накопленное отклонение ряда х от среднего значения Х
Эрик Найман усовершенствовал формулу Херста для выборки случайных величин, представленной небольшим числом наблюдений [8].
Данную формулу мы будем использовать для дальнейших расчетов.
Исследования многих ученых показывают, что динамике рыночных цен соответствуют показатели Hurst (H) намного больше 0.5. Это говорит о том, что динамика рыночных цен не является случайной. Указанная динамика обусловлена двумя основными причинами.
- Рыночная информация не сразу учитывается в ценах, так как у инвесторов нет равного доступа к информации.
- По прошествии определенного временного периода, влияние информации на цены финансовых активов снижается. Это выражается в наличии на рынке известного психологического феномена - память рынка.
Для того, чтобы выявить инерционностъ финансового рынка рассчитаем показатель Hurst для валют – EUR / USD по ценам закрытия, интервал – 1 день, количество наблюдений – 20. Исходные данные для расчета были взяты с официального сайта FOREX - FXTMPIRE // http://ru.fxempire.com/currencies/eur-usd/tools/historical-data/. [9]
Исследования многих экономистов показали, что нормированный размах логарифмов изменений случайных рядов намного меньше, чем нормированный размах логарифмов изменений линейных (растущих или нисходящих) рядов.
В результате, показатели Херста, рассчитанные по логарифмам изменений линейных рядов данных достигают значительных величин. Если рассмотреть данные, показывающие признаки трендовости и рассчитать по ним логарифмы изменений, то показатель Херста такого ряда значительно превысит единицу. Это будет типичным случаем для трендовых рядов. Поэтому мы будем использовать классическую модель расчета показателя Херста – по исходным данным. Результаты расчета представлены в Таблице 2.
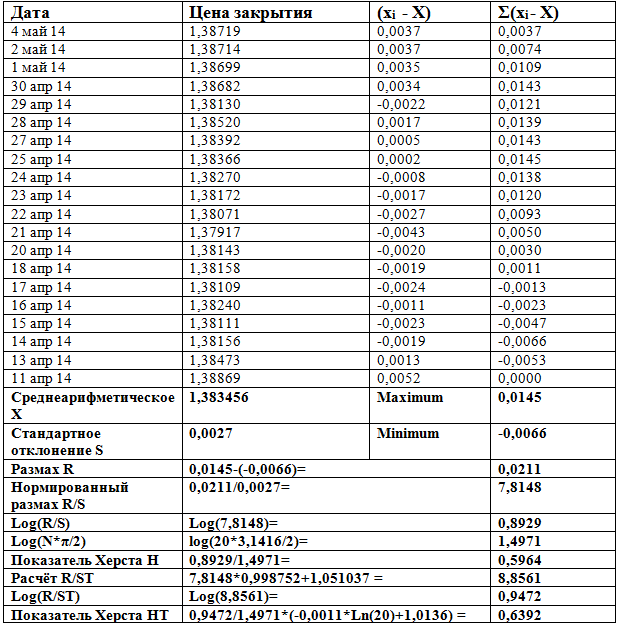
Таблица 2 – Результаты расчёт показателя Hurst по ценам закрытия валютной пары EUR/USD (N=20) [составлено автором]
Результаты проведенного исследования показывают, что рынок обладает памятью на коротком временном интервале, так как Н = 0,5964.
Таким образом, проведенные нами расчеты показали, что рыночные явления и экономические индикаторы не являются случайными явлениями. Рынок инерционен, т.е. обладает памятью. Структура финансовых рынков обусловлена структурой финансовых продуктов, механизм функционирования которых регулируется финансовыми институтами. Чем многообразнее финансовые продукты, тем более устойчивы финансовые рынки. Разнообразные виды финансовых продуктов образуют фрактальную структуру рынка. Это, в свою очередь, подтверждает справедливость гипотезы фрактального рынка (Fractal Market Hypothesis, FMH), которая является альтернативой гипотезы эффективного рынка (Effective Market Hypothesis, EMH).
Литература
- Eugene F. Fama Foundations of Finance: Portfolio Decisions and Securities Prices. - Basic Books, 1976. - 395 p.
- Bachelier L., Theory of Speculation. in Cootner P. edition, The Random Character of Stock Market Price. Cambridge: MIT Press, 1964. (Originally published in 1900.)
- Mandelbrot, Benoit B., J.W. van Ness. 1968. “Fractional Brownian Motion, Fractional Noises and Application.” SIAM Review 10: 422–37
- Peters, Edgar E. 1994. Fractal Market Analysis: Applying Chaos Theory to Investment and Economics. New York: John Wiley and Sons
- Alchian, A. and Woodward, S. (1988), “The firm is dead; long live the firm: A review of Oliver Williamson’s The Economic Institutions of Capitalism”, Journal of Economic Literature, Vol. 26 No. 1, pp.65-79
- Strambach, S. (2010), “Path dependence and path plasticity: The co-evolution of institutions and innovation”, in Boschma, R. and Martin, R. (eds.), The Handbook of Evolutionary Economic Geography, Edward Elgar, Cheltenham, pp. 406-431
- Hurst, H.E. (1951), “Long-term storage of reservoirs: an experimental study”, Transactions of the American Society of Civil Engineers, Vol. 116, pp. 770-799
- Найман Э. Как покупать дешево и продавать дорого: Пособие для разумного инвестора - М.: «Альпина Паблишерз», 2011. – 552 с.
- Официальный сайт FOREX - FXTMPIRE // http://ru.fxempire. com/currencies/eur-usd/tools/historical-data/
References
- Eugene F. Fama Foundations of Finance: Portfolio Decisions and Securities Prices. - Basic Books, 1976. - 395 p.
- Bachelier L., Theory of Speculation. in Cootner P. edition, The Random Character of Stock Market Price. Cambridge: MIT Press, 1964. (Originally published in 1900.)
- Mandelbrot, Benoit B., J.W. van Ness. 1968. “Fractional Brownian Motion, Fractional Noises and Application.” SIAM Review 10: 422–37
- Peters, Edgar E. 1994. Fractal Market Analysis: Applying Chaos Theory to Investment and Economics. New York: John Wiley and Sons
- Alchian, A. and Woodward, S. (1988), “The firm is dead; long live the firm: A review of Oliver Williamson’s The Economic Institutions of Capitalism”, Journal of Economic Literature, Vol. 26 No. 1, pp.65-79
- Strambach, S. (2010), “Path dependence and path plasticity: The co-evolution of institutions and innovation”, in Boschma, R. and Martin, R. (eds.), The Handbook of Evolutionary Economic Geography, Edward Elgar, Cheltenham, pp. 406-431
- Hurst, H.E. (1951), “Long-term storage of reservoirs: an experimental study”, Transactions of the American Society of Civil Engineers, Vol. 116, pp. 770-799
- Najman Je. Kak pokupat' deshevo i prodavat' dorogo: Posobie dlja razumnogo investora - M.: «Al'pina Pablisherz», 2011. – 552 s.
- Oficial'nyj sajt FOREX - FXTMPIRE // http://ru.fxempire. com/currencies/eur-usd/tools/historical-data/