ПРОГНОЗИРОВАНИЕ ДЕФОРМАЦИЙ СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ ПО РЕЗУЛЬТАТАМ ГЕОДЕЗИЧЕСКИХ НАБЛЮДЕНИЙ
Поздышева О.Н.
ORCID: 0000-0002-6647-2970, кандидат философских наук, Самарский государственный технический университет
ПРОГНОЗИРОВАНИЕ ДЕФОРМАЦИЙ СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ ПО РЕЗУЛЬТАТАМ ГЕОДЕЗИЧЕСКИХ НАБЛЮДЕНИЙ
Аннотация
Практические результаты геодезических измерений позволяют не только определить деформации конструкций и инженерных сооружений, но и прогнозировать процесс деформаций. Прогнозирование деформаций сооружений и отдельных его частей производится на основе информации, которую получают различными методами. Обработка такой информации осуществляется методами математической статистики с привлечением аппарата теории вероятностей. В данной публикации приводятся наиболее частые применяемые методы прогнозирования деформаций строительных конструкций по результатам геодезических наблюдений.
Ключевые слова: деформация, геодезия, функция, геодезические наблюдения.
Pozdysheva O.N.
ORCID: 0000-0002-6647-2970, PhD in Philosophy, Samara State Technical University
FORECASTING OF DEFORMATIONS OF BUILDING STRUCTURES ACCORDING TO THE RESULTS OF GEODETIC OBSERVATIONS
Abstract
The practical results of geodetic measurements allow not only to determine deformation of structures and engineering structures, but also to predict the process of deformation. Forecasting of deformations of buildings and its parts are manufactured on the basis of information which is obtained by various methods. Processing of such data is carried out by methods of mathematical statistics with the involvement of the probability theory. This publication provides the most common used methods of forecasting of deformations of building structures according to the results of geodetic observations.
Keywords: deformation, geodesy, function, and geodetic observations.
Геодезические наблюдения за деформациями строительных конструкций в результате представляют собой разрозненную количественную форму объективной и точной информации о сложном взаимодействии строительных конструкций с грунтовым основанием и внешней средой. Данная информация является основой для вычисления путем математического моделирования закономерностей развития процессов деформации, проверяемых не только геодезическими, но и комплексными натурными наблюдениями. Полученные закономерности деформаций отдельных сооружений для конкретных локальных условий могут быть обобщены на уровнях, выбранных по заданным критериям однотипности сооружений, однородности инженерно-геологических условий грунтов оснований и близости характера воздействий внешней среды
Практические результаты геодезических измерений могут обрабатываться вероятностно-статистическими методами. Это позволяет не только определить деформации конструкций и инженерных сооружений, но и прогнозировать процесс деформаций с широким применением математических методов анализа.
Современные сооружения в большинстве своем отличаются сложными конструктивными решениями – большой этажностью при относительно малой площади основания или же наличием ответственных технологических линий, располагающихся на значительной территории. Это приводит к тому, что для изучения деформаций отдельных элементов конструкций, технологического оборудования и всего сооружения на них устанавливают специальные деформационные марки, за которыми в последствии наблюдают. Таким образом у организации, проводящей геодезические наблюдения, собирается материал, содержащий большой объем важной информации как непосредственно о полученной опорной геодезической сети, (деформационной сети) и качестве выполненных наблюдений. В итоге и состоянии конструкций сооружения в целом и его элементов в отдельности.
Таким образом ограничиваться классической методикой систематизации и анализа явно не достаточно. Необходимо применение новых, инновационных средств и аппарата математической статистики.
В классических учебниках по геодезии под математической обработкой результатов наблюдений за деформациями строительных конструкций и его частями обычно понимается:
- Выявление конкретных деформационных характеристик строительных конструкций в целом и отдельных его частей.
- Оценка достоверности полученных результатов наблюдений.
- Систематизация информационного материала наблюдений с целью установления количественных характеристик, описывающих основные закономерности в процессе деформаций.
- Обнаружение зависимости между деформациями и причинами, их обуславливающими, с целью последующего прогнозирования деформационных характеристик строительных конструкций.
Для прогнозирования деформаций строительных конструкций применяется много методов:
- метод множественного корреляционного анализа;
- метод наименьших квадратов;
- метод случайных функций;
- метод Шарле;
- логарифмический ряд и другие.
Метод множественного корреляционного и регрессионного анализа
Этот метод позволяет выявить характер и степень взаимосвязи между показателями, являющимися случайными величинами, а так же обнаружить насколько изменение одной переменной (фактора) в среднем влияет на изменение другой переменной (результативного признака).
При применении корреляционного анализа определяется один показатель, характеризующий степень тесноты взаимосвязи показателей. А при применении регрессионного анализа строится модель регрессии в виде математической функции, которая показывает влияние факторов на некоторый показатель.
Таким образом производя эти анализы одновременно получаем более точные достоверные результаты при наличии большого экспериментального материала со значительным количеством возмущающих факторов.
Решение осуществляется следующим порядком:
- задается матрица со всеми исходными данными;
- исходная матрица преобразовывается в матрицу сумм произведений, по которой составляется корреляционная матрица;
- матрица сумм произведений преобразовывается в матрицу сумм произведений уклонений.
Критерий Фишера (F- критерий) определяет отношение дисперсии функций к остаточной сумме квадратов, которая определяется по разностям фактических и вычисленных значений функций.
Критерий Фишера устанавливает степень надежности результатов, полученных по уравнению регрессии. По таблицам Фишера можно оценивать достоверность результатов с надежностью 99%.
Метод наименьших квадратов
Этот метод является самым распространенным и максимально разработанным из-за своей простоты и эффективности методов оценки линейных параметров. При этом, применяя этот метод, следует соблюдать определенную осторожность, так как построенные с его использованием модели могут не удовлетворять целому ряду требований к качеству их параметров и, поэтому недостаточно “хорошо” отображать закономерности развития процесса.
При применении метода наименьших квадратов аппроксимацию полученных результатов можно осуществить следующими способами:
- линейная функция;
- квадратичная функция;
- периодическая функция;
- параболическое аппроксимирование;
- периодическое аппроксимирование.
Решение задачи всегда начинается с построения графика. Кривая зависимости показывает приблизительно вид искомой функции. Это может быть прямая, парабола какого-то порядка или кривая, показывающая периодический характер функции.
Во многих случаях практически графическое решение задачи, заключающееся в построении сглаживающей (аппроксимирующей) кривой или прямой, оказывается достаточным. Более строгое решение задачи осуществляется параметрическим способом.
Линейная функция
Это такая зависимость, что функция прямо пропорциональна аргументу. Пусть известно, что функция имеет вид:
![]()
где k0 и k1 требуется определить, для чего измерен ряд значений х (i =1,…, n) и соответственных им значений y . Ошибками измерений значений х пренебрегают, ввиду их малости, и учитывают только ошибки измеренных значений у. Если поставить условием, чтобы в минимум обращалась сумма квадратов расстояний заданных точек (х, у) от искомой прямой, то такая прямая будет называться вероятнейшей прямой.
Квадратичная функция
Функция имеет вид:
![]()
и выражается графической параболой 2-го порядка.
В данном случае не известны коэффициенты ![]() ; число измерений должно быть n > 3. Для упрощения вычислений переносят начало координат в точку с координатами
; число измерений должно быть n > 3. Для упрощения вычислений переносят начало координат в точку с координатами
![]()
![]()
где х и у – результаты измерений.
Функция в этой системе координат примет вид ![]()
Задача свелась к нахождению неизвестных k1, k2 и k3.
Так же, как и при линейной аппроксимации. Размерности для х и у выбираются так, чтобы уклонения были по абсолютной величине близки к единице.
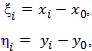
Функция имеет вид
![]()
где х изменяется от 0 до 2mπ через равные промежутки Ϭ=![]() , где n – четное число, причем m – целое число. Так производят наблюдения периодических функций. Число наблюдений N=2mn.
, где n – четное число, причем m – целое число. Так производят наблюдения периодических функций. Число наблюдений N=2mn.
Так как значения х изменяются через равные промежутки Ϭ=![]() , (n – число четное), то значения аргумента х располагаются симметрично относительно осей координат. Нормальные уравнения имеют вид
, (n – число четное), то значения аргумента х располагаются симметрично относительно осей координат. Нормальные уравнения имеют вид
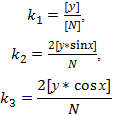
Непосредственно по этим формулам находят искомые коэффициенты.
Логарифмический ряд
Логарифмическим рядом называется метод дифференцирования функций, вначале которого находится логарифм функции, а затем подсчитывается производная от него. Такой прием разрешает максимально эффективно вычислить производные степенных и рациональных функций.
Для построения логарифмического ряда обычно пользуются формулой:
![]()
Список литературы / References
- Большаков В.Д. Теория математической обработки геодезических измерений / В.Д. Большаков, П.А. Гайдаев. - М.: Недра, 1977 - 367 с.
- Вентцель Е.С. Теория вероятностей. / Е.С. Вентцель. - М.: Наука, 1964 - 576 с.
- Колмогоров А.Н. Основные понятия теории вероятностей. / А.Н. Колмогоров. - М.: Недра, 1968 - 437 с.
- Мазмишвили А.И. Способ наименьших квадратов. / А.И. Мазмишвили - М.: Недра, 1968 - 437 с.
- Маринин Е.И. Вероятностно-статистические методы обработки результатов геодезических наблюдений за деформациями сооружений. / Е.И. Маринин, В.Н. Ткачук. // Вопросы инженерной геодезии в строительстве: межвузовский сборник научных трудов. – Самара: СГАСУ - 2013. – С. 102
Список литературы на английском языке / References in English
- Bolshakov V. D., Teorija matematicheskoi obrabotki geodezicheskih izmerenii [the Theory of mathematical rocessing of geodetic measurements] / V. D. Bolshakov, P. A. Gaydayev. - M.: Nedra, 1977 - 367 p. [in Russian]
- Wentzel E. S. Teorija verojatnostei [probability Theory]. / E. S. Wentzel. - M.: Nauka, 1964 – 576 p. [in Russian]
- Kolmogorov, A. N. Osnovnye ponjatija verojatnostei [Basic concepts of probability theory. / A. N. Kolmogorov. - M.: Nedra, 1968 - 437 p. [in Russian]
- Mazmishvili A. I. Sposob naimenshih kvadratov [Method of least squares]. / Mazmishvili A. I. - M.: Nedra, 1968 - 437 p. [in Russian]
- Marinin, E. I., Verojatnosno-statisticheskie metody obrabotki rezultatov geodezicheskih nablydenii za deformacijami [Probabilistic-statistical methods of processing of results of geodetic observations for deformations of structures]. / E. I. Marinin, V. N. Tkachuk. // [Questions of engineering geodesy in construction: interuniversity collection of scientific works. – Samara: SGASU] - 2013. – P. 102. [in Russian]
