ПОВЫШЕНИЕ ПОКАЗАТЕЛЕЙ КАЧЕСТВА СЛЕДЯЩЕГО ЭЛЕКТРОПРИВОДА ПЕРЕМЕННОГО ТОКА С СИНХРОННЫМ ДВИГАТЕЛЕМ НА ОСНОВЕ АДАПТИВНОГО МОДАЛЬНОГО УПРАВЛЕНИЯ С УЧЕТОМ ИСПОЛЬЗОВАНИЯ КОРРЕКЦИИ СТАТИЧЕСКИХ ХАРАКТЕРИСТИК
ПОВЫШЕНИЕ ПОКАЗАТЕЛЕЙ КАЧЕСТВА СЛЕДЯЩЕГО ЭЛЕКТРОПРИВОДА ПЕРЕМЕННОГО ТОКА С СИНХРОННЫМ ДВИГАТЕЛЕМ НА ОСНОВЕ АДАПТИВНОГО МОДАЛЬНОГО УПРАВЛЕНИЯ С УЧЕТОМ ИСПОЛЬЗОВАНИЯ КОРРЕКЦИИ СТАТИЧЕСКИХ ХАРАКТЕРИСТИК
Научная статья
Нгуен Минь Хонг1, *, Фам Туан Тхань2, Ву Хыу Тхик3
1, 2, Технический университет им. Ле Куй Дона, Ханой, Вьетнам;
3 Ханойский промышленный университет, Ханой, Вьетнам
* Корреспондирущий автор (nguyenhaihong2007[at]yahoo.com.vn)
АннотацияВ статье представлен метод повышения показателей качества следящего электропривода на основе синхронного двигателя с постоянными магнитами используя адаптивное модальное управление с учетом использования коррекции статических характеристик. Указанный электропривод широко применяется в различных областях техники, например, в приводе исполнительных органов роботов, в мобильных устройствах, в промышленных и военных оборудованиях, где требуются простота конструкция, низкая энергопотребность. Выполнено моделирование системы в среде Matlab-Simulink. Полученные результаты показали, что при применении представленного метода, обеспечена точность слежения системы, подвергающейся влиянию нелинейных факторов.
Ключевые слова: следящий электропривод, коррекция статических характеристик, адаптивное модальное управление.
IMPROVEMENT OF QUALITY INDICATORS OF THE AC SERVO DRIVE WITH SYNCHRONOUS MOTOR BASED ON ADAPTIVE MODAL CONTROL CONSIDERING CORRECTION OF STATIC CHARACTERISTICS
Research article
Nguyen Minh Hong1, *, Pham Tuan Thanh2, Vu Huu Thich3
1, 2, Le Quy Don Technical University, Ha Noi, Viet Nam;
3 Hanoi University of Industry, Ha Noi, Viet Nam
* Corresponding author (nguyenhaihong2007[at]yahoo.com.vn)
AbstractThe paper presents the method for improving the quality indicators of a servo drive based on a permanent magnet synchronous motor using adaptive modal control considering the use of static characteristics correction. The specified servo drive is widely used in various fields of technology, for example, in the drive of executive bodies of robots, in mobile devices, in industrial and military equipment, where simplicity of construction and low energy consumption are required. The system was simulated in the Matlab-Simulink environment. The results showed that when applying the presented method, the tracking accuracy of the system subjected to the influence of nonlinear factors can be ensured.
Keywords: servo drive, correction of static characteristics, adaptive modal control.
- Введение
Качество следящего электропривода, в частности позиционного следящего электропривода (ПСЭП), зависит от выбора исполнительных органов и методов управления. В ПСЭП малой мощности часто применяли двигатель постоянного тока с коллектором и двигатель асинхронный двухфазного тока. В настоящее время использование синхронного двигателя с постоянными магнитами (ДСсПМ) стало перспективной тенденцией, так как он обладает достоинством двух вышеуказанных двигателей [6], [7].
В ПСЭП управление ДСсПМ осуществляется различными методами, такими как дискретное управление [7], [8], непрерывное управление [11], частотное управление [2], [10], векторное управление [2], [11]. Среди вышеперечисленных методов векторное управление обеспечивает наиболее высокое качество [11]. Однако, в системах малой мощности применение векторного управления оказывается менее подходящим из-за сложной структуры и большего объёма расчёта микроконтроллера. Поэтому в системах малой мощности применяется метод коррекции статических характеристик, сущность которого заключается в том, что напряжение ud, в разнице от метода uq векторного управления – создаётся из регулятора тока Rid, образуется путём косвенного вычисления из напряжения и некоторого параметра двигателя, зависящего от конкретного алгоритма расчёта. В сравнении с классическим векторным управлением, метод коррекции статических характеристик даёт не меньшее качество при достаточно простой структуре системы.
Другая проблема, рассматриваемая в статье, заключается в том, что в системе позиционного следящего электропривода малой мощности всегда присутствует коробка передач, что приводит к сложности конструкции механической части. Вследствие сильной нелинейности (зазор зубчатых колёс, коэффициент упругости, момент трения) точность слежения системы значительно уменьшается. Анализ опубликованных исследований показывает, что для преодоления указанной проблемы при обеспечении простоты структуры управления для систем малой мощности, предпочтительным является использование адаптивного модального управления. Согласно проведённому исследованию [6], адаптивное управление электромеханическими системами наилучшим образом осуществляется по контуру скорости, где плотно находятся источники возмущения, вызывающие погрешности слежения. Затем синтез регулятора положения следует выполнять с использованием методов стандартных функций для достижения требуемой точности управления для всей системы.
- Алгоритм коррекции статических характеристик системы управления
Алгоритм коррекции статических характеристик системы построен на основе известные системы уравнений, описывающей ДСсПМ [3], [9] (в системе уравнений векторные величины обозначены без подчёркивания):
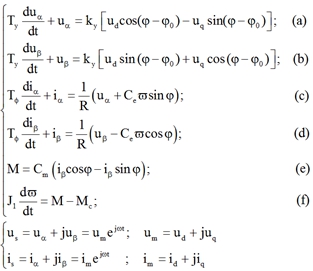 (1)
(1)
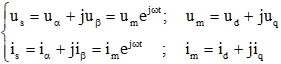 (2)
(2)
где ![]() : соответственно, проекции вектора напряжения статора
: соответственно, проекции вектора напряжения статора ![]() на оси системы координат dq и системы координат αβ;
на оси системы координат dq и системы координат αβ; ![]() - проекции вектора тока статора
- проекции вектора тока статора ![]() на оси и системы координат αβ;
на оси и системы координат αβ; ![]() ; – комплексные амплитуды векторов напряжения тока статора в системе координат dq;
; – комплексные амплитуды векторов напряжения тока статора в системе координат dq; ![]() – коэффициент усиления усилителя мощности;
– коэффициент усиления усилителя мощности; ![]() – угловое положение ротора двигателя;
– угловое положение ротора двигателя; ![]() – начальный настраиваемый угол датчика положения ротора; Ce, Cm – соответственно, коэффициент противоэлектродвижущей силы и коэффициент момента двигателя,
– начальный настраиваемый угол датчика положения ротора; Ce, Cm – соответственно, коэффициент противоэлектродвижущей силы и коэффициент момента двигателя, ![]() – соответственно, электромагнитная и электронная постоянные времени двигателя; J1 - момент инерции; М - крутящий момент двигателя; Mc – момент сопротивления; R – фазовое сопротивление;
– соответственно, электромагнитная и электронная постоянные времени двигателя; J1 - момент инерции; М - крутящий момент двигателя; Mc – момент сопротивления; R – фазовое сопротивление; ![]() – угловая скорость двигателя.
– угловая скорость двигателя.
Подставляв (1a), (1b) и затем (1c), (1d) в (2), мы получили соотношение для вычисления тока im и его составляющего по оси d. При заданном условии ![]() найден закон управления с учетом использования коррекции статических характеристик, имеющий следующий вид:
найден закон управления с учетом использования коррекции статических характеристик, имеющий следующий вид:
![]()
- Модель системы следящего электропривода с учетом конструкции механической части
Модель механической части систем электропривода имеет сложную конструкцию [8] и при их синтезе часто использована двухмассовая модель [6]. Объединяя систему дифференциальных уравнений, описывающую двигатель, с системой уравнений, описывающей механическую часть, которая была применима в работе [3], получаем систему дифференциальных уравнений, описывающую механическую систему:
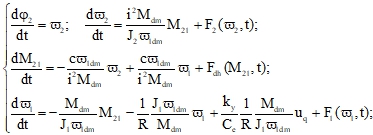 (4)
(4)
где ![]() – соответственно упругий момент, номинальный момент двигателей и момент сопротивления; i - передаточное отношение коробки передач;
– соответственно упругий момент, номинальный момент двигателей и момент сопротивления; i - передаточное отношение коробки передач;![]() – угловые скорости, углы поворота и моменты инерции двигателя и рабочего органа; R – фазовое сопротивление;
– угловые скорости, углы поворота и моменты инерции двигателя и рабочего органа; R – фазовое сопротивление; ![]() – функции, зависящие от неопределённых, изменяющихся по времени факторов, которые включают в себе зубчатый зазор, упругость и трение в механической части; с – коэффициент упругости; Mms1, Mms2 – моменты трения в двигателе и в рабочем механизме, соответственно.
– функции, зависящие от неопределённых, изменяющихся по времени факторов, которые включают в себе зубчатый зазор, упругость и трение в механической части; с – коэффициент упругости; Mms1, Mms2 – моменты трения в двигателе и в рабочем механизме, соответственно.
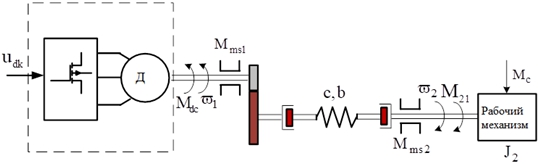
Рис. 1 – Модель механической системы с учетом упругости, зубчатого зазора и трения
- Построение модального адаптивного звена управления
Согласно [6], модальное адаптивное звено управления предназначено для контура скорости, где плотно находятся источники возмущения, вызывающие погрешности слежения системы.
4.1. Построение наблюдателя состояния
Вектор состояния механической системы может быть написано в следующем виде: ![]() , где – вектор измеренных переменных состояния,
, где – вектор измеренных переменных состояния, ![]() – вектор неизмеренных переменных состояния. Для достижения простоты структуры модального адаптивного звена управления, будет разработан наблюдатель состояния пониженного порядка. Наблюдаемые величины включают в себя момент упругости, скорость вращения двигателя и скорость рабочего механизма (
– вектор неизмеренных переменных состояния. Для достижения простоты структуры модального адаптивного звена управления, будет разработан наблюдатель состояния пониженного порядка. Наблюдаемые величины включают в себя момент упругости, скорость вращения двигателя и скорость рабочего механизма (![]() ). Такие величины являются информацией для обновления параметров адаптивного регулятора. Кроме того, наблюдатель состояния должен создавать адаптивные сигналы в соответствии с алгоритмом, выбранным из условий, чтобы в системе, находящейся в процессе оценки состояния, возникает скользящий режим. Входными величинами наблюдателя являются угловое положение рабочего механизма и управляющее напряжение двигателя uq.
). Такие величины являются информацией для обновления параметров адаптивного регулятора. Кроме того, наблюдатель состояния должен создавать адаптивные сигналы в соответствии с алгоритмом, выбранным из условий, чтобы в системе, находящейся в процессе оценки состояния, возникает скользящий режим. Входными величинами наблюдателя являются угловое положение рабочего механизма и управляющее напряжение двигателя uq.
После линейного преобразования системы уравнений (4), механическая система сводится к форме, удовлетворяющей условиям управляемости и наблюдаемости. Система (4) переписана в виде двух уравнений состояния для измеренных переменных состояния и неизмеренных переменных состояния. Затем на основе метода обобщённого модального управления Роппенекера, представленного в [4], для точной оценки неизмеренных факторов (по сравнению с практикой) через матрицу наблюдения L, приводится к модели наблюдателя состояния адаптивный сигнал z (t), имеющий следующий вид:
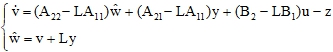
где ![]() – вектор состояния наблюдателя, матрица наблюдения L выбирается на основе динамического процесса наблюдателя; A22, A11, A21, B1 и B2 – матрицы, выделившиеся из функциональных матриц A и B при описании системы в пространстве состояний [4],
– вектор состояния наблюдателя, матрица наблюдения L выбирается на основе динамического процесса наблюдателя; A22, A11, A21, B1 и B2 – матрицы, выделившиеся из функциональных матриц A и B при описании системы в пространстве состояний [4],
![]()
Исходя из вышеуказанных уравнений и в соответствии [12], погрешность оценки ![]() имеет следующий вид:
имеет следующий вид:
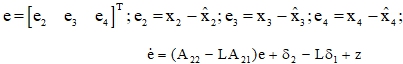
где ![]() – функциональные векторы функций, вызывающие вектор ошибок при выполнении линеаризованного преобразования модели двигателя. Для обеспечения устойчивости наблюдателя состояния использован метод функции Ляпунова. Была выбрана функция Ляпунова V=0,5eTPe, где P - положительно определённая матрица.
– функциональные векторы функций, вызывающие вектор ошибок при выполнении линеаризованного преобразования модели двигателя. Для обеспечения устойчивости наблюдателя состояния использован метод функции Ляпунова. Была выбрана функция Ляпунова V=0,5eTPe, где P - положительно определённая матрица.
Полная производная функции V c учётом (6) имеет вид:![]()
где ![]() ; Q – положительно определённая диагональная матрица, выбранная в соответствии с размером области сходимости процесса оценки состояния. Для возникновения в системе скользящего режима, происходящего в процессе регулирования наблюдателя при оценке состояния, адаптивный закон управления выбирается следующим образом:
; Q – положительно определённая диагональная матрица, выбранная в соответствии с размером области сходимости процесса оценки состояния. Для возникновения в системе скользящего режима, происходящего в процессе регулирования наблюдателя при оценке состояния, адаптивный закон управления выбирается следующим образом:
![]() (7)
(7)
где ![]() ; h – выбранный расчётный параметр при моделировании или эксперименте. Из приведённого выше анализа имеем систему уравнений, описывающую наблюдатель состояния, в следующем виде:
; h – выбранный расчётный параметр при моделировании или эксперименте. Из приведённого выше анализа имеем систему уравнений, описывающую наблюдатель состояния, в следующем виде:
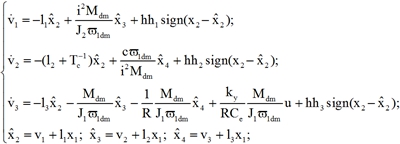 (8)
(8)
4.2. Построение структуры системы управления
Задача управления – выбрать закон адаптивного управления u(t) так, чтобы вектор состояния x(t) был стабильным в близости к образному вектору состояния xm(t), создаваемому из выбранной образной модели. В случае достижения цели наблюдения за состоянием, для устранения вектора ошибки δ, основываясь на методе модального управления, представленном в [4], вводим адаптивный сигнал в выражение закона модального управления (6). В результате получили закон адаптивного модельного управления следующего вида:
![]() (9)
(9)
где K1, K2 – соответствующие блоки модальной матрицы K; K3 – постоянная матрица, определённая из отношения между линеаризованной моделью объекта и образной моделью; g(t) – m-мерный вектор заданных воздействий (например, настраиваемый сигнал, программа управления ...); B2 – матрица, элементы которой зависят от постоянных времени механической части; ![]() – вектор измеряемых переменных. Элементы модальной матрицы K, матрицы наблюдения L, вычислительной матрицы H найдены при выборе требуемого характеристического многочлена образной модели и при условиях, обеспечивающих устойчивость системы. Элементы адаптивного сигнала отвечают за равномерность элементов вектора z. Для этого использованы фильтры, имеющие маленькую постоянную времени
– вектор измеряемых переменных. Элементы модальной матрицы K, матрицы наблюдения L, вычислительной матрицы H найдены при выборе требуемого характеристического многочлена образной модели и при условиях, обеспечивающих устойчивость системы. Элементы адаптивного сигнала отвечают за равномерность элементов вектора z. Для этого использованы фильтры, имеющие маленькую постоянную времени ![]() .
.
Структурная схема модального адаптивного звена управления показана на рис. 2.
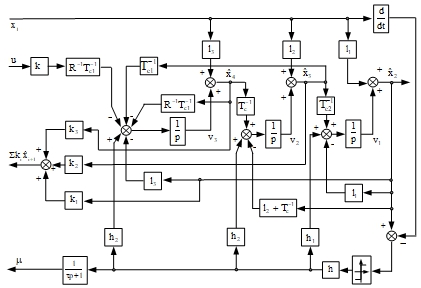
Рис. 2 – Структурная схема адаптивного звена управления
- Cинтез регулятора положения
Предполагая, что построенная выше система адаптивного модального управления для контура скорости удовлетворяет требованию управления, приблизительно можно считать, что наблюдатель состояния независим от системы. На основе структурной схемы двигателя, имеющей вид передаточной функции [5], и с целью устранения статических ошибок, регулятор положения, синтезированный модульным оптимальным методом, является пропорционально-интегральным звеном (ПИ), которое имеет следующие коэффициенты:
![]() (10)
(10)
где: ![]() – передаточный коэффициент по скорости; Tm – электромеханическая постоянная времени двигателя, c – коэффициент упругости;
– передаточный коэффициент по скорости; Tm – электромеханическая постоянная времени двигателя, c – коэффициент упругости; ![]() – передаточный коэффициент датчика положения.
– передаточный коэффициент датчика положения.
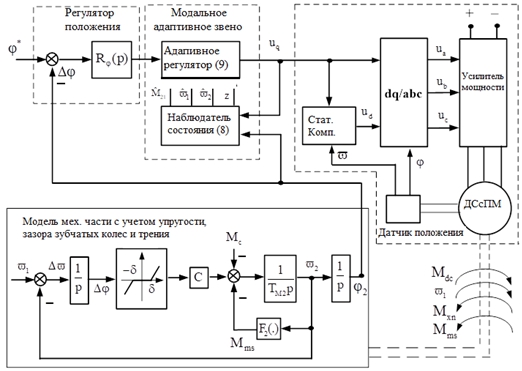
Рис. 3 – Блок-схема следящего электропривода с модальным адаптивным управлением с учетом использования коррекции статических характеристик ДСсПМ
- Моделирование и оценка результатов
6.1. Параметры моделирования
R = 5,0; U = 12 В; n = 2150 мин-1; Пусковой момент: 0,324 Нм; номинальная мощность Pdm = 18 Вт; Tm = 160 мс; Tm = 0,07 мс; Сm= 0,12 Нм / А; Ce = 0,12 В.сек. / рад; момент инерции: 2,3,10-4 кг.м2; ky = 13,5; Ty = 0,0001; L = 0,0035; Се = 0,12; р = 4; кB = 0,00001; Сm = 0,12; Т = 0,0007; kcd = 5,0; k = 6; k1 = 0,335; k2 = 0,005; k3 = 0,5; l1 = 550; l2 = 50; l3 = 1200; h = 5; h1 = 10; h2 = 10; h3 = 3,5; Tc1 = 0,00012; Tc2 = 0,00086; Тс = 0,0001; t = 0,0001;
6.2. Схема моделирования
Схема моделирования строится для среды Matlab-Simulink. При этом модели двигатели, регулятора и усилителя построены на основе дифференциальных уравнений, которые широко используются в [2, 7, 9, 10, 11]; построение статического компенсатора осуществлено по алгоритму (3), модальное адаптивное звено построено из выражений (8) и (9).
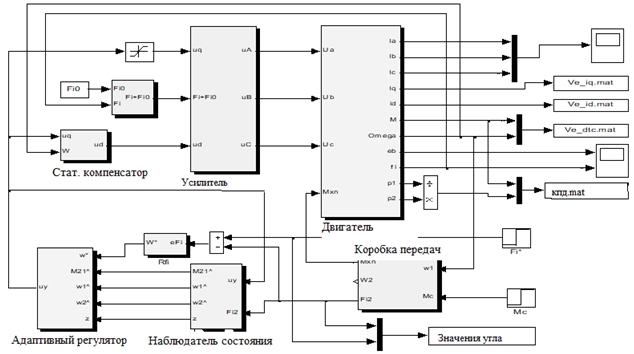
Рис. 4 – Схема моделирования системы в среде Simulink
6.3. Результаты моделированияНа рисунках 5, 6, 7, 8 приведены результаты моделирования в двух случаях: с использованием предложенной системы управления (левые графики) и с использованием классического пропорционально-интегрально-дифференцирующего регулятора (графики б) при одинаковых условиях.
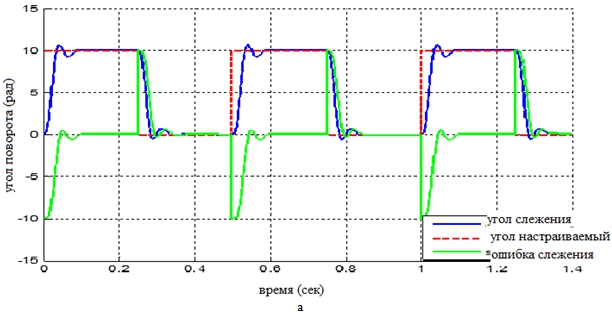
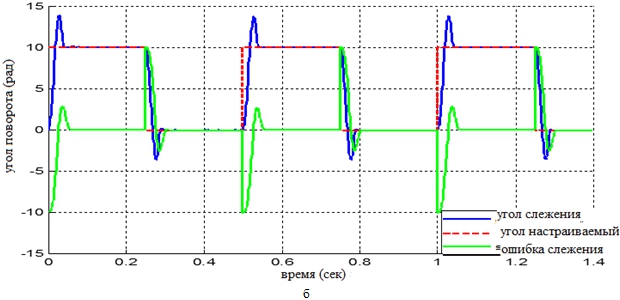
Рис. 5 – Значение угла поворота при зазоре зубчатых колёс ![]() рад
рад
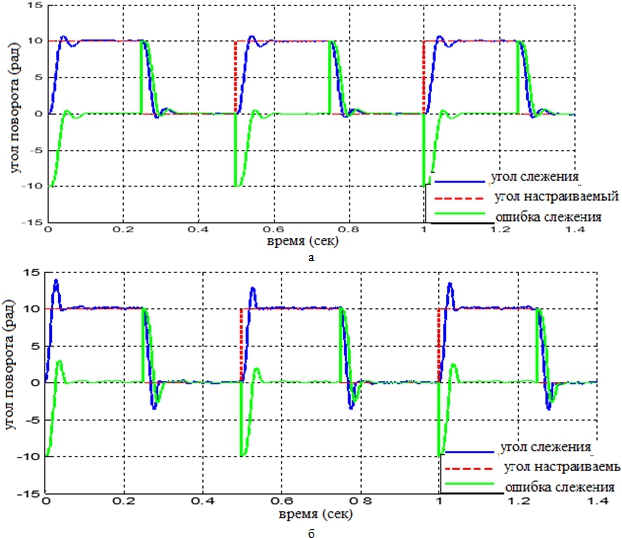
Рис. 6 – Значение угла поворота при зазоре зубчатых колёс ![]() рад
рад
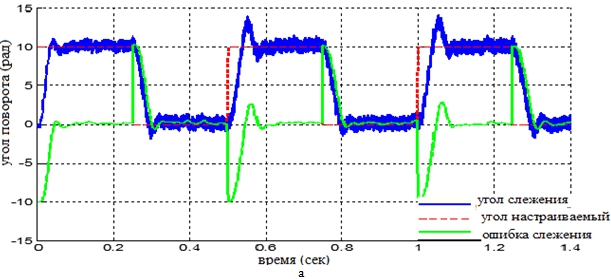
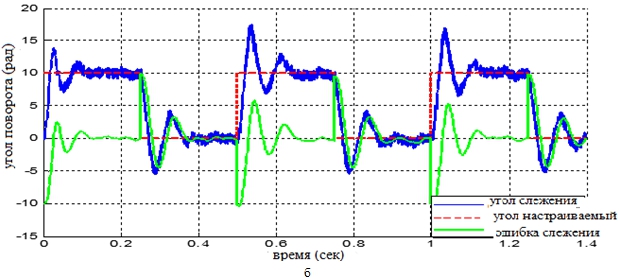
Рис. 7 – Значение угла поворота при зазоре зубчатых колёс ![]() рад
рад
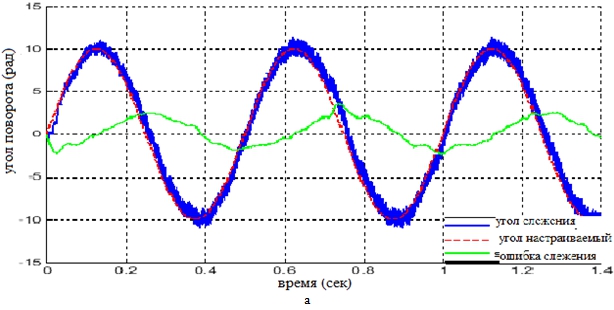
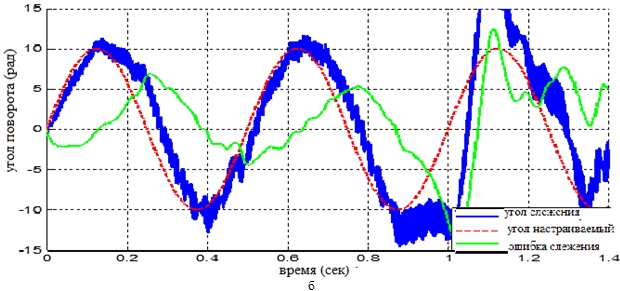
Рис. 8 – Значение угла поворота при зазоре зубчатых колёс рад. и входном синусоидальном сигнале
Графики средней ошибки слежения, приведённые на рисунках 5, 6, 7 и 8 показали, что при малом зазоре зубчатых колёс коробки передач ошибка слежения в статическом режиме приблизительна к нулю, при увеличении указанного зазора до достаточно большого значения точность слежения обеспечивается только в модальной адаптивной системе, а в системе ПИД-регулятора ошибка слежения относительно велика. Анализ полученных результатов показывает, что использование модального адаптивного регулятора с коррекцией статических характеристик обеспечило точность слежения системы, подвергающейся влияния нелинейных факторов. Модальный адаптивный регулятор способен обнаруживать и погасить упругие колебания, уменьшать влияние нелинейных факторов, значительно повышать динамическое и статическое качество следящей системы.
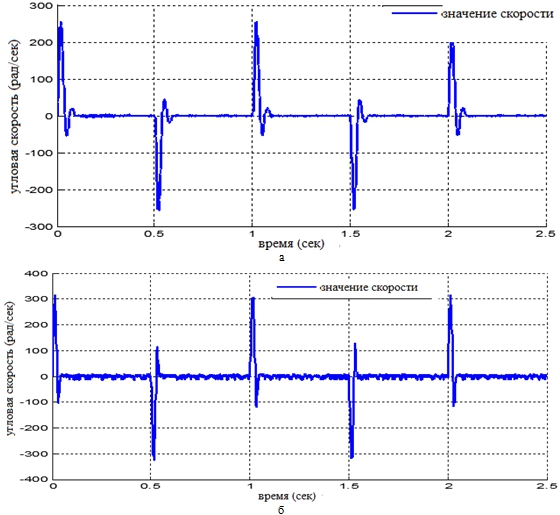
Рис. 9 – Значение скорости при зазоре зубчатых колес рад
Результаты моделирования, приведенные на рисунке 9, показали, что модальная адаптивная система работает более «плавно» по сравнению с обычной ПИД ситемой.
- Заключение
В статье представлен метод повышения показателей качества следящего электропривода на основе синхронного двигателя с постоянными магнитами используя адаптивное модальное управление с учетом использования коррекции статических характеристик. Результаты моделирования утверждают высокую надёжность алгоритмов управления. Более того, по сравнению с классическим ПИД-регулятором при эквивалентных условиях точность слежения представленной системы всегда обеспечивается, и при случае, когда на систему сильно влияют нелинейные факторы, вызванные структурой механической части.
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Ву Хыу Тхик Повышение качества управления системы следящего электропривода на основе синхронного двигателя малой мощности с использованием алгоритма управления коррекции статических характеристик. /Ву Хуй Тхик, Фам Туан Тхань/, Журнал науки и техники, Военно-техническая академия, № 170. – август 2015г., С. 47-53.
- Нгуен Фунг Хоанг. Управление электроприводом трехфазного переменного тока / Нгуен Фунг Хоанг, Изд. Образования, 1998г.
- Методы повышения качества электропривода с зазором на основе устойчивого стабильного управления/ диссертация.– 2013г.
- Нгуен Зоан Фыок Устойчивое оптимальное управление/ Нгуен Зоан Фыок, Фам Суан Минь // Издательство науки и техники – 2010г.
- Буй Куок Кхань Управление электроприводом/ Буй Куок Кхань, Нгуен Ван Лиен, Фам Куок Хай и др. Изд. Науки и техники, 2010г.
- Электромеханические системы с адаптивным и модальным управлением / Ю. А. Борцов, Н. Д. Поляхов, В. В. Путов. — Л.: Энергоатомиздат. Ленингр., 1984. — 216 с.
- Бут Д.А. Бесконтактные электрические машины: Учебное пособие для электромеханик. и электроэнергия. спец. Вузов / Бут Д.А. -Высшая школа, 1990.
- Овчинников И.Е. Вентильные электрические двигатели и привод на их основе (малая и средняя мощность): курс лекций [текст] / Овчинников И.Е. - СПб.: КОРОНА-Век, 2007, 336с.
- Самохвалов Д.В. Коррекция статических характеристик электропривода с вентильным двигателем малой мощности и микропроцессорным управлением. Автореферат диссертации на соискание ученой степени кандидата технических наук / Самохвалов Д.В. Санкт-Петербург, – 2010.
- Соколовский Г. Г. Электроприводы переменного тока с частотным регулированием / Соколовский Г. Г. Учебник. Москва.: 2006.
- Виноградов А.Б. Векторное управление электроприводами переменного тока / Виноградов А.Б. // ГОУВПО «Ивановский государственный энергетический университет имени В.И. Ленина».– Иваново, 2008.-298 с.
- Gang Tao Adaptive Control Design and Analysis / Gang Tao University of Virginia 2003.
Список литературы на английском языке / References in English
- Wu Huu Thik Povysheniye kachestva upravleniya sistemy sledyashchego elektroprivoda na osnove sinkhronnogo dvigatelya maloy moshchnosti s ispol'zovaniyem algoritma upravleniya korrektsii staticheskikh kharakteristik [Improving the quality of control of a servo drive system based on a low-power synchronous motor using a control algorithm for correcting static characteristics] / Wu Hui Thik, Fam Tuan Than // Zhurnal nauki i tekhniki, Voyenno-tekhnicheskaya akademiya [Journal of Science and Technology, Military Technical Academy] , No. 170. – August 2015, P. 47-53. [in Russian]
- Nguyen Fung Hoang. Upravleniye elektroprivodom trekhfaznogo peremennogo toka [Control of an electric drive of three-phase alternating current] / Nguyen Fung Hoang. Ed. Education, 1998 [in Russian]
- Metody povysheniya kachestva elektroprivoda s zazorom na osnove ustoychivogo stabil'nogo upravleniya [Methods of improving the quality of the electric drive with a gap based on sustainable stable management / dissertation]. – 2013. [in Russian]
- Nguyen Zoan Fyok Ustoychivoye optimal'noye upravleniye/ [Sustainable Optimal Control] / Nguyen Zoan Fyok, Fam Xuan Min // Publishing House of Science and Technology] – 2010. [in Russian]
- Bui Kuok Khan Upravleniye elektroprivodom [Electric Drive Control] / Bui Kuok Khan, Nguyen Van Lien, Fam Kuok Hai and others // Ed. Science and Technology, 2010 [in Russian]
- Elektromekhanicheskiye sistemy s adaptivnym i modal'nym upravleniyem [Electromechanical systems with adaptive and modal control] / Yu. A. Bortsov, N.D. Polyakhov, V.V. Putov. – L.: Energoatomizdat. Leningrad, 1984. – 216 p. [in Russian]
- Booth D.A. Beskontaktnyye elektricheskiye mashiny: Uchebnoye posobiye dlya elektromekhanik. i elektroenergiya. spets. Vuzov [Contactless electric machines: a manual for an electrician. and electricity. specialist. Universities] / Booth D.A. – High School, 1990. [in Russian]
- Ovchinnikov I.E. Ventil'nyye elektricheskiye dvigateli i privod na ikh osnove (malaya i srednyaya moshchnost'): kurs lektsiy [Valve electric motors and drives based on them (low and medium power): lecture course [text].] / Ovchinnikov I.E. – St. Petersburg: CROWN-Century, 2007, 336 p. [in Russian]
- Samokhvalov D.V. Korrektsiya staticheskikh kharakteristik elektroprivoda s ventil'nym dvigatelem maloy moshchnosti i mikroprotsessornym upravleniyem [Correction of the static characteristics of an electric drive with a low-power valve motor and microprocessor control] / Samokhvalov D.V. // Abstract of dissertation for the degree of PhD in Engineering. St. Petersburg, - 2010. [in Russian]
- Sokolovsky G.G. Elektroprivody peremennogo toka s chastotnym regulirovaniyem. Uchebnik [Electric drives of alternating current with frequency regulation. Textbook] / Sokolovsky G.G. Moscow: 2006. [in Russian]
- Vinogradov A.B. Vektornoye upravleniye elektroprivodami peremennogo toka [Vector control of AC electric drives] / Vinogradov A.B. // GOUVPO “Ivanovo State Power Engineering University named after V.I. Lenin.” – Ivanovo, 2008. – 298 p. [in Russian]
- Gang Tao Adaptive Control Design and Analysis / Gang Tao, University of Virginia 2003.
