СМЕШАННАЯ ЗАДАЧА ДЛЯ ОДНОГО КВАЗИЛИНЕЙНОГО ПАРАБОЛИЧЕСКОГО УРАВНЕНИЯ С ГИСТЕРЕЗИСОМ
СМЕШАННАЯ ЗАДАЧА ДЛЯ ОДНОГО КВАЗИЛИНЕЙНОГО ПАРАБОЛИЧЕСКОГО УРАВНЕНИЯ С ГИСТЕРЕЗИСОМ
Научная статья
Исаева С.Э.*
ORCID: 000-0002-0872-1350,
Бакинский Государственный Университет, Баку, Азербайджан
* Корреспондирующий автор (isayevasevda[at]rambler.ru)
Аннотация
В данной работе рассматривается начально-краевая задача для одного квазилинейного параболического уравнения с запоминающим оператором в ограниченной области с достаточно гладкой границей. Доказана теорема о существовании решений рассматриваемой начально-краевой задачи с запоминающим оператором. Для доказательства этой теоремы использован метод дискретизации по времени. Доказана также единственность решений этой задачи, если запоминающий оператор является гистерезисной нелинейностью типа обобщенного люфта.
Ключевые слова: квазилинейное параболическое уравнение, запоминающий оператор, гистерезис, обобщенный люфт.
MIXED PROBLEM FOR ONE QUASILINEAR PARABOLIC EQUATION WITH HYSTERESIS
Research article
Isaeva S.E.*
ORCID: 000-0002-0872-1350,
Baku State University, Baku, Azerbaijan
* Corresponding author (isayevasevda[at]rambler.ru)
Abstract
The paper considers an initial-boundary value problem for a quasilinear parabolic equation with a memory operator in a bounded domain with a sufficiently smooth boundary. A theorem on the existence of solutions of the initial-boundary value problem with a memory operator is proved. We used the method of discretization with respect to time to prove this theorem. The uniqueness of the solutions of this problem is also proved if the memory operator is a hysteresis nonlinearity of the generalized backlash type.
Keywords: quasilinear parabolic equation, memory operator, hysteresis, generalized backlash.
Введение
Дифференциальные уравнения с запоминающим оператором, особенно уравнения с гистерезисом имеют большое значение среди нелинейных дифференциальных уравнений с частными производными. Понятие гистерезисного оператора впервые было введено в [1]. Смешанные задачи с гистерезисными нелинейностями изучены, например, в работах [2], [3], [4]. В данной работе рассматривается начально-краевая задача для одного квазилинейного параболического уравнения с запоминающим оператором. В случае отсутствия запоминающего оператора, эта задача исследована, например в [5]. Разрешимость такой задачи без нелинейного слагаемого ![]() , исследована в работе [6]. В данной работе доказана теорема о существовании решений рассматриваемой задачи. Доказана также единственность решений этой задачи, если запоминающий оператор является гистерезисной нелинейностью типа обобщенного люфта. Отметим, что смешанные задачи с такими гистерезисными нелинейностями изучены, например, в работах [7], [8].
, исследована в работе [6]. В данной работе доказана теорема о существовании решений рассматриваемой задачи. Доказана также единственность решений этой задачи, если запоминающий оператор является гистерезисной нелинейностью типа обобщенного люфта. Отметим, что смешанные задачи с такими гистерезисными нелинейностями изучены, например, в работах [7], [8].
Постановка задачи и основные результаты
Пусть ![]() ограниченная область с достаточно гладкой границей Г В области
ограниченная область с достаточно гладкой границей Г В области ![]() рассмотрим квазилинейное параболическое уравнение:
рассмотрим квазилинейное параболическое уравнение:
![]() (1)
(1)
с граничным условием
![]() (2)
(2)
и с начальным условием
![]() , (3)
, (3)
где ![]() и нелинейный оператор F действует из пространства
и нелинейный оператор F действует из пространства ![]() пространство измеримых функций, действующих из в
пространство измеримых функций, действующих из в ![]() . Предполагается, что F является запоминающим оператором, который действует в каждой точке
. Предполагается, что F является запоминающим оператором, который действует в каждой точке ![]() независимо, то есть
независимо, то есть ![]() зависит от
зависит от ![]() и не зависит от
и не зависит от ![]() для
для ![]() .
.
Пусть оператор F удовлетворяет следующим условиям:
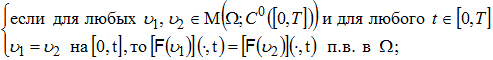 (4)
(4)
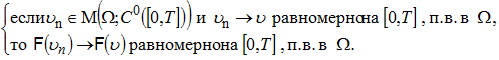 (5)
(5)
Пусть ![]() . Предполагаем, что
. Предполагаем, что
![]() , (6)
, (6)
![]() (7)
(7)
Определение
Функция ![]()
и удовлетворяющая для любого ![]() п.в. в равенству
п.в. в равенству
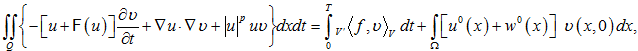 (8)
(8)
называется решением задачи (1)-(3).
Из определения решения следует, что
![]() (9)
(9)
откуда
![]() ;
;
поэтому ![]() и (9) удовлетворяется в
и (9) удовлетворяется в ![]() п. в. на
п. в. на ![]() . Интегрирование по частям в соотношении (8) дает следующее:
. Интегрирование по частям в соотношении (8) дает следующее:
в ![]() (в смысле распределений). (10)
(в смысле распределений). (10)
В свою очередь из (9) и (10) получается соотношение (8).
Предположим, что оператор F удовлетворяет также условиям:
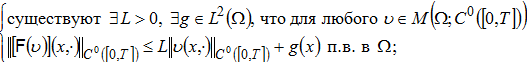 (11)
(11)
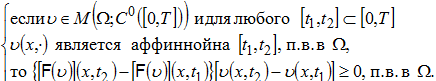 (12)
(12)
Теорема 1. Пусть выполняются условия (4)-(7), (11), (12). Тогда задача (1)-(3) имеет по крайней мере одно решение, для которого имеет место:
![]() (13)
(13)
Доказательство. Применим метод дискретизации по переменному t (см.[6]).
Разбивая отрезок [0,t] точками ![]() частей, обозначая
частей, обозначая
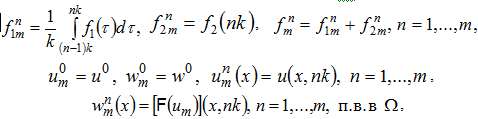
![]() линейная интерполяция по времени
линейная интерполяция по времени ![]() для
для ![]() и аналогичным образом определяя
и аналогичным образом определяя ![]() , рассмотрим задачу
, рассмотрим задачу
![]() (14)
(14)
![]() . (15)
. (15)
Покажем, что эта задача может быть решена шаг за шагом. Предположим, что ![]() известны для любого
известны для любого ![]() и рассмотрим задачу определения
и рассмотрим задачу определения ![]() . Функция является
. Функция является ![]() аффинной на отрезке
аффинной на отрезке ![]() , почти для всякого
, почти для всякого ![]() ; поэтому
; поэтому ![]() зависит только от
зависит только от ![]() , которое известно, и от
, которое известно, и от ![]() , которое должно быть определено. Поэтому
, которое должно быть определено. Поэтому
![]() .
.
Пусть
![]() . (16)
. (16)
Согласно (16), ![]() и из (11) получаем, что
и из (11) получаем, что
![]() . (17)
. (17)
для любого ![]() .
.
Определим оператор . Согласно (5) и (17) имеем
![]() аффинно ограничен и сильно непрерывен. (18)
аффинно ограничен и сильно непрерывен. (18)
Из (12) получается, что
![]()
для любого ![]() . Из последнего неравенства и из (17), получаем, что существуют такие постоянные
. Из последнего неравенства и из (17), получаем, что существуют такие постоянные ![]() (зависящие от m, n но не от υ), что
(зависящие от m, n но не от υ), что
![]() (19)
(19)
![]()
Если не учесть фиксированные индексы m и n, то уравнение (14) можем записать в виде:
![]() (20)
(20)
где ![]() . Для доказательства существования хотя бы одного решения этого уравнения воспользуемся стандартной процедурой. Пусть
. Для доказательства существования хотя бы одного решения этого уравнения воспользуемся стандартной процедурой. Пусть ![]() - последовательность конечномерных подпространств, покрывающих V; для любого
- последовательность конечномерных подпространств, покрывающих V; для любого ![]() рассмотрим следующую конечномерную задачу:
рассмотрим следующую конечномерную задачу:
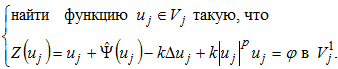 (21)
(21)
Согласно (18), ![]() является сильно непрерывным оператором. Из (19) (а также из того факта, что для
является сильно непрерывным оператором. Из (19) (а также из того факта, что для ![]() выполняется неравенство
выполняется неравенство ![]() - некоторые постоянные) получается, что этот оператор удовлетворяет следующему условию:
- некоторые постоянные) получается, что этот оператор удовлетворяет следующему условию:
![]() (22)
(22)
Отсюда получаем, что задача (21) имеет хотя бы одно решение (по одному варианту теоремы Брауэра о неподвижной точке, [5], гл. I, раздел 4.3). Умножая (21) на и используя (22), получаем, что последовательность ![]() равномерно ограничена в V. Следовательно, существует такая функция u и можно выделить такую подпоследовательность
равномерно ограничена в V. Следовательно, существует такая функция u и можно выделить такую подпоследовательность ![]() .
.
Согласно компактному вложению: ![]() и (18) имеем
и (18) имеем
![]()
Поэтому переходя к пределу в (21) ![]() , получаем (20); то есть существует функция u, которая является решением уравнения (20) (или (14)).
, получаем (20); то есть существует функция u, которая является решением уравнения (20) (или (14)).
Чтобы получить априорные оценки, умножим обе части (14) на ![]() . Тогда суммируя по
. Тогда суммируя по ![]() для любого
для любого ![]() и интегрируя по Ω, получим:
и интегрируя по Ω, получим:
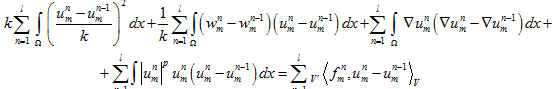 (23)
(23)
Согласно (12) имеем
![]() (24)
(24)
кроме того
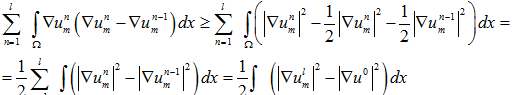 (25)
(25)
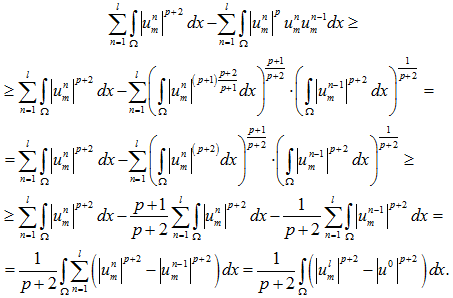 (26)
(26)
Учитывая (24), (25), (26) в (23), имеем
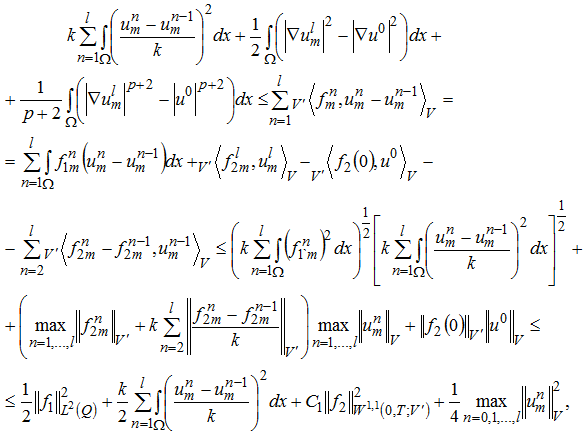 (27)
(27)
где постоянная ![]() не зависит от m. Так как (27) справедливо для любого
не зависит от m. Так как (27) справедливо для любого ![]() , то проведя несложные преобразования, получим, что
, то проведя несложные преобразования, получим, что
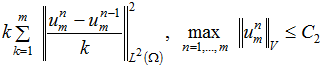 , (28)
, (28)
где постоянная ![]() не зависит от m.
не зависит от m.
Пусть
![]()
и определим ![]() аналогичным образом. Тогда из (14) и (28) имеем:
аналогичным образом. Тогда из (14) и (28) имеем:
![]() (29)
(29)
![]() . (30)
. (30)
Так как ![]() (с непрерывным вложением), то согласно (11) и (30)
(с непрерывным вложением), то согласно (11) и (30)
![]() (31)
(31)
и поскольку ![]() порождает отображение
порождает отображение ![]() , то легко проверить, что
, то легко проверить, что
![]() . (32)
. (32)
Из соотношений (29)-(32) получаем, что
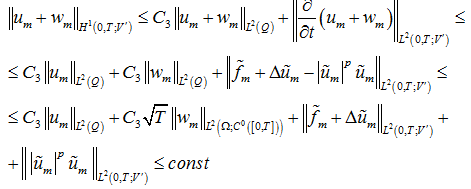 (33)
(33)
Известно, что если D - Банахово пространство и при ![]() , то
, то
![]()
(см. [9]); кроме того, если D рефлексивно, или ![]() сепарабельно, то
сепарабельно, то
![]() .
.
Используя этот факт для ![]() и оценку (33), заключаем, что существуют функции u,w такие, что (после выделения быть может под последовательности) при
и оценку (33), заключаем, что существуют функции u,w такие, что (после выделения быть может под последовательности) при ![]()
![]() (34)
(34)
![]() (35)
(35)
![]() (36)
(36)
![]() (37)
(37)
где ![]() .
.
Учитывая (34)-(37), переходим к пределу в (29) при ![]() и получаем (9); легко получается и (10). И это, как мы уже отметили, приводит к (8).
и получаем (9); легко получается и (10). И это, как мы уже отметили, приводит к (8).
Известно ([10], глава 4, стр. 378), что
![]()
с непрерывными вложениями (последнее вложение также компактное). Поэтому, выделяя быть может очередную подпоследовательность, имеем:
![]() равномерно на
равномерно на ![]() , п. в. в Ω.
, п. в. в Ω.
Тогда, согласно (5), ![]() равномерно на
равномерно на ![]() , п. в. в Ω.
, п. в. в Ω.
Так как ![]() является линейной интерполяцией по времени от
является линейной интерполяцией по времени от ![]() для почти всех
для почти всех ![]() , то имеем
, то имеем ![]() равномерно на
равномерно на ![]() , п. в. в Ω.
, п. в. в Ω.
Поэтому согласно (36) имеем: ![]() п. в. в Q. Из (11) получается, что
п. в. в Q. Из (11) получается, что ![]() сходится в
сходится в![]() .
.
Теорема 1 доказана.
Теперь рассмотрим задачу (1)-(3) при дополнительном условии, что F является гистерезисной нелинейностью типа обобщенного люфта (см. [6]).
Пусть для функций ![]() удовлетворяется условие
удовлетворяется условие
![]() (38)
(38)
для любого ![]() .
.
Обозначим через E гистерезисный оператор обобщенного люфта (см.[6], глава III). Зафиксируем некоторое ![]() и предположим, что
и предположим, что
![]() (39)
(39)
для любого ![]() и для любого
и для любого ![]() .
.
Оператор удовлетворяет условиям (4)-(5), (11)-(12). Для этого оператора удовлетворяются также неравенство
![]() п. в. на
п. в. на ![]() ,
,
и следующее
Неравенство Гильперта ([6], глава III). Пусть
![]()
и ![]() - измеримая функция, такая, что
- измеримая функция, такая, что ![]() п. в. на
п. в. на ![]() . Если
. Если ![]() , то
, то
![]()
Теорема 2. Пусть ![]() - липшицево непрерывны, аффинно ограничены и удовлетворяют условию (38). Определим F как в (39) и предположим, что
- липшицево непрерывны, аффинно ограничены и удовлетворяют условию (38). Определим F как в (39) и предположим, что
![]() п. в. на
п. в. на ![]() .
.
Если ![]() - соответствующие решения задачи (1)-(3) с
- соответствующие решения задачи (1)-(3) с ![]() , то для любого
, то для любого ![]() удовлетворяются неравенство
удовлетворяются неравенство
![]() (40)
(40)
Доказательство. Пусть
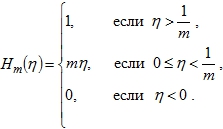
Согласно теореме III. 2.3 (см. [1]), ![]() .
.
Так как
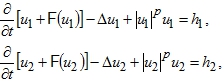
то
![]()
откуда умножая на ![]() и интегрируя по Ω, имеем
и интегрируя по Ω, имеем
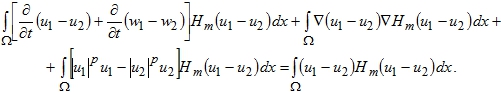 (41)
(41)
Так как
![]()
п. в. на ![]() и
и
![]()
то из (41) получаем
![]() (42)
(42)
Теперь переходим к пределу при ![]() . Существует функция
. Существует функция ![]() такая, что
такая, что ![]() п. в. в Q. Кроме того
п. в. в Q. Кроме того ![]() п. в. в Q, где
п. в. в Q, где
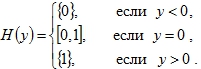
Тогда из (42) получаем, что
![]() (43)
(43)
Так как в силу неравенства Гильперта удовлетворяется неравенство
![]()
то из (43) имеем
![]()
откуда получается (40).
Теорема 2 доказана.
Теорема 3. Пусть
![]()
функции ![]() липшицево непрерывны, аффинно ограничены и удовлетворяют условию (38), а F определяется как в (39). Тогда задача (1)-(3) с f=h имеет единственное решение, которое удовлетворяет условию (13).
липшицево непрерывны, аффинно ограничены и удовлетворяют условию (38), а F определяется как в (39). Тогда задача (1)-(3) с f=h имеет единственное решение, которое удовлетворяет условию (13).
Доказательство. Эта теорема является прямым следствием теорем 1 и 2.
Заключение
Дифференциальные уравнения с запоминающим оператором, особенно уравнения с гистерезисом имеют большое значение среди нелинейных дифференциальных уравнений с частными производными, которые встречаются в физике, механике, биологии, химии, экономике и в других областях науки; гистерезисные явления часто встречаются также в теории трения, в ферромагнетизме, в теории сверхпроводимости. Особую трудность имеют уравнения с гистерезисом, если гистерезисный оператор находится под оператором дифференцирования по переменной t. В этой статье методом дискретизации по времени исследована разрешимость смешанной задачи для одного квазилинейного параболического уравнения с запоминающим оператором; доказана также единственность решений этой задачи, при дополнительном условии, что запоминающий оператор является гистерезисной нелинейностью типа обобщенного люфта.
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Красносельский М.А. Системы с гистерезисом // М.А. Красносельский, А.В. Покровский. - М.: Наука, 1983.-272 c.
- Mielke A. Rate-independent systems. Theory and application / A. Mielke, T. Roubicek // Applied Mathematical Sciences. - vol. 193. - Springer, New York. - 2015. - 660 p.
- Visintin A. Quasilinear hyperbolic equations with hysteresis // Ann. Inst. H. Poincare. Analyse nonlineaire. - 19. - 2002. - P. 451-476.
- Visintin A. Mathematical models of hysteresis / In: The Science of Hysteresis (G. Bertotti, I. Mayergoyz, eds.) Elsevier. - 2006. - chap.1. - P. 1-123.
- Лионс Ж.Л. Некоторые методы решения нелинейных краевых задач / Ж.Л. Лионс. - М.: Мир. - 1972. - 588 c.
- Visintin A. Differential Models of Hysteresis / A. Visintin. - Springer, 1993. - 411 p.
- Kopfova J. Uniqueness theorem for a Cauchy problem with hysteresis // Proceedings of the American Mathematical Society. - 1999. - vol. 127. - No 12. - PP. 3527-3532.
- Kopfova J. Periodic solutions and asymptotic behavior of a PDE with hysteresis in the source term // Rocky Mountain Journal of Mathematics. - 2006. - vol. 36. - No 2. - P. 539-554.
- Ларькин Н.А. Нелинейные уравнения переменного типа / Н.А. Ларькин, В.А. Новиков, Н.Н. Яненко - Наука, Новосибирск, 1983. - 269 c.
- Лионс Ж.Л. Неоднородные граничные задачи и их приложения / Ж.Л. Лионс, Э. Мадженес. - М.: Мир, 1971.-357 c.
Список литературы на английском языке / References in English
- Krasnoselskii M.A. Sistemy s gisterezisom [Systems with Hysteresis] // M.A. Krasnoselski, A.V. Pokrovsky. – M.: Nauka, 1983. [in Russian]
- Mielke A. Rate-independent systems. Theory and application / A. Mielke, T. Roubicek // Applied Mathematical Sciences. – Vol. 193. – Springer, New York. – 2015. – 660 p.
- Visintin A. Quasilinear hyperbolic equations with hysteresis // Ann. Inst. H. Poincare. Analyse nonlineaire. – 19. – 2002. – P. 451-476.
- Visintin A. Mathematical models of hysteresis / In: The Science of Hysteresis (G. Bertotti, I. Mayergoyz, eds.) Elsevier.-2006. – Ch.1. – P. 1-123.
- Lions J.L. Nekotorye metody resheniya nelineinykh kraevykh zadach [Some Methods for Solving Nonlinear Boundary Value Problems] / J.L. Lions – M.: Mir. – 1972. – 588 p. [in Russian]
- Visintin A. Differential Models of Hysteresis / A. Visintin. – Springer, 1993. -411 p.
- Kopfova J. Uniqueness theorem for a Cauchy problem with hysteresis // Proceedings of the American Mathematical Society. – 1999. – Vol. 127. – No 12. – P. 3527-3532.
- Kopfova J. Periodic solutions and asymptotic behavior of a PDE with hysteresis in the source term // Rocky Mountain Journal of Mathematics. - 2006. – Vol. 36. – No 2. – P. 539-554.
- Larkin N.A. Nelineinye uravneniya peremennogo tipa [Nonlinear Equations of Variable Type] / N.A. Larkin, V.A. Novikov, N.N. Yanenko. – Nauka, Novosibirsk, 1983. – 269 p. [in Russian]
- Lions J.L. Neodnorodnye granichnye zadachi i ikh prilozheniya [Nonhomogeneous Boundary Value Problems and Their Applications] / J.L. Lions, E. Magenes. – M.: Mir, 1971. – 357 p. [in Russian]
