ПОСТРОЕНИЕ ОБЛАСТЕЙ ПРИТЯЖЕНИЯ ПРИ ВЫРОЖДЕНИИ СИНГУЛЯРНО ВОЗМУЩЕННЫХ УРАВНЕНИЙ
DOI: https://doi.org/10.23670/IRJ.2018.75.9.001
ПОСТРОЕНИЕ ОБЛАСТЕЙ ПРИТЯЖЕНИЯ ПРИ ВЫРОЖДЕНИИ СИНГУЛЯРНО ВОЗМУЩЕННЫХ УРАВНЕНИЙ
Научная статья
Алыбаев К.С.1, Мурзабаева А.Б.2, *
1 ORCID: 0000-0002-7962-534X,
Жалал-Абадский государственный университет, Жалал-Абад, Кыргызстан;
2 ORCID: 0000-0003-0694-6633,
Ошский технологический университет, Ош, Кыргызстан
* Корреспондирующий автор (aytbu.murzabaeva[at]mail.ru)
Аннотация
В работе проведен анализ систем сингулярно возмущенных обыкновенных дифференциальных уравнений. Дается обзор известных результатов по рассматриваемому вопросу и на их основе обоснована степень актуальности исследуемой задачи. Рассматривается система сингулярно возмущенных обыкновенных дифференциальных уравнений с аналитическими функциями в комплексной области. Вырожденная система, соответствующая рассматриваемой системе, теряет единственность при вырождении. Для анализа решения начальной задачи по малому параметру введено понятие области притяжения решения вырожденной системы. Поставленная задача сводится к отысканию областей притяжения. С привлечением линии уровня гармонических функций в комплексной области построены области и доказано, что они являются областями притяжения рассматриваемых решений вырожденной системы.
Ключевые слова: сингулярное возмущение, вырожденные уравнения, гармоническая функция, линии уровня, область притяжения, асимптотика.
CONSTRUCTION OF DOMAINS OF ATTRACTION AT DEGENERATION OF SINGULARLY PERTURBED EQUATIONS
Research article
Alibaev K.S.1, Murzabaeva A.B.2, *
1 ORCID: 0000-0002-7962-534X,
Jalal-Abad State University, Jalal-Abad, Kyrgyzstan;
2 ORCID: 0000-0003-0694-6633,
Osh Technological University, Osh, Kyrgyzstan
* Corresponding author (aytbu.murzabaeva[at]mail.ru)
Abstract
The paper presents the analysis of singularly perturbed systems of ordinary differential equations. The overview of known results on the considered issue is given and the degree of relevance of the problem under investigation is substantiated based on them. We consider a system of singularly perturbed ordinary differential equations with analytic functions in the complex domain. A degenerate system corresponding to the system under consideration loses its uniqueness under degeneracy. In order to analyze the solution of the initial problem with respect to a small parameter, we introduce the notion of the domain of attraction of a solution of a degenerate system. The problem is reduced to finding the domains of attraction. Domains are constructed with the use of the level line of harmonic functions in the complex domain, and it is proved that they are domains of attraction of the solutions of the degenerate system under consideration.
Keywords: singular perturbation, degenerate equations, harmonic function, level lines, domain of attraction, asymptotics.
Введение
Многочисленные задачи математики, математической и теоретической физики, техники приводят к исследованию дифференциальных уравнений или их систем с малыми параметрами при старших производных. Такие классы уравнений получило название сингулярно возмущенные.
Примеры сингулярно возмущенных уравнений прикладного характера приведены в [1].
Асимптотическими разложениями решений сингулярно возмущенных уравнений занимались многие исследователи. Об этом подробнее можно ознакомиться в [2], [3]. Сингулярно возмущенные уравнения в комплексных областях рассмотрены редко. В этом направлении из ранних работ можно назвать [4], [5], [6], [11], [12]. К более поздним работам относятся [8], [9], [10].
В [8] рассматриваются сингулярно возмущенные обыкновенные дифференциальные уравнения (системы) с аналитическими функциями в некоторых комплексных областях. Рассматриваемые области содержат отрезки действительной оси. Присоединённые уравнения (системы) заданных уравнений (систем) имеют одну точку покоя, причём она устойчива по Ляпунову в части отрезка действительной оси и неустойчива в другой части этого отрезка.
Доказано, что решения начальных задач рассматриваемых уравнений (систем) при потере устойчивости не сразу уходит от возникшей неустойчивой точки покоя, а в течении конечного времени остается вблизи него. Это явление получило название «затягивание потери устойчивости при динамических бифуркациях».
В [9], [10] доказано, сингулярно возмущенные обыкновенные дифференциальные уравнения (системы) с аналитическими функциями в комплексных областях обладают рядом специфических свойств. В частности доказано существование так называемых «погранслойных линий», которые можно рассматривать как частные случаи линий Стокса. Погранслойные линии разделяют рассматриваемые комплексные области на части. В одних частьях решение стремится к решению вырожденного уравнения (системы) по ![]() , а в другой части не ограничена, а в самой погранслойной линии решение не имеет предела по ε. Также доказано, явление «затягивание потери устойчивости» происходит при определенных условиях на правые части рассматриваемых уравнений (систем). Таким образом, существование погранслойных линий специфическое свойство сингулярно возмущенных уравнений (систем) с аналитическими функциями, а «затягивание потери устойчивости» явление происходящее при благоприятных условиях.
, а в другой части не ограничена, а в самой погранслойной линии решение не имеет предела по ε. Также доказано, явление «затягивание потери устойчивости» происходит при определенных условиях на правые части рассматриваемых уравнений (систем). Таким образом, существование погранслойных линий специфическое свойство сингулярно возмущенных уравнений (систем) с аналитическими функциями, а «затягивание потери устойчивости» явление происходящее при благоприятных условиях.
В [8], [10] исследования проведены в предположении, что вырожденные уравнения (системы), соответствующие рассматриваемым уравнениям (системам) в комплексных областях имеют одно единственное решение. Уравнения (системы), когда вырожденные уравнения (системы) имеют несколько решений ранее не рассматривались.
Постановка задачи
Пусть рассматривается система
![]() (1)
(1)
с начальным условием
![]() , (2)
, (2)
где ![]() - односвязная область;
- односвязная область; ![]() и её внутренняя точка.
и её внутренняя точка.
![]() .
.
![]() – комплекснозначная аналитическая функция по переменным (t, z) в некоторой области H переменных (t, z).
– комплекснозначная аналитическая функция по переменным (t, z) в некоторой области H переменных (t, z).
При ε=0 из (1) получим вырожденную систему
![]() (3)
(3)
Предложим, что система (3) имеет изолированные решения (корни) ![]() .
.
Далее: ![]() - означает пространство аналитических функций в Ω.
- означает пространство аналитических функций в Ω.
Запись ![]() будет означать, что для любого t из Ω справедливо утверждение σ(t).
будет означать, что для любого t из Ω справедливо утверждение σ(t).
Определение 1: Если ![]() , то решения
, то решения ![]() называются изолированными в Ω.
называются изолированными в Ω.
Определение 2: Если: 1. Существует область ![]() содержащая точку
содержащая точку ![]() .
.
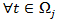 существует
существует 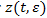 - решение задачи (1)-(2).
- решение задачи (1)-(2).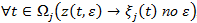 , то область
, то область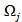 назовем областью притяжения решения
назовем областью притяжения решения 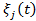 .
.
Далее область притяжения обозначим ![]() .
.
Предметом наших исследований будут формулировка условий на правые части системы (1), при которых существуют области притяжения.
Для наглядости рассмотрим случай, когда
![]() .
.
Предположим выполнения условия ![]() .
.
Для этого случая каждое вырожденное уравнение имеет по два решения, которые обозначим
![]() .
.
Из полученных решений составим следующие решения для вырожденной системы
![]()
Задача: Существуют ли области притяжения ![]() ?
?
Предварительные обозначения и построения
Рассмотрим функции ![]() и введем обозначения
и введем обозначения ![]() . Согласно U1 функции
. Согласно U1 функции ![]() - гармонические.
- гармонические.
По определению ![]() . Тогда существуют линии уровня
. Тогда существуют линии уровня ![]() проходящие через точку
проходящие через точку ![]() .
.
U.3 Пусть линии уровня ![]() не имеют общих точек, кроме точки
не имеют общих точек, кроме точки ![]() .
.
Линии ![]() область Ω делят на четыре части. Эти части обозначим
область Ω делят на четыре части. Эти части обозначим ![]() .
.
Если учесть U.2, то линия ![]() не имеет кратных точек и область Ω делит на две части в каждом из которых
не имеет кратных точек и область Ω делит на две части в каждом из которых ![]() , причем равенство имеет место только для точек
, причем равенство имеет место только для точек ![]() . Аналогичное имеет место для
. Аналогичное имеет место для ![]() . Условие U.3 обеспечивает существование единственной области, где
. Условие U.3 обеспечивает существование единственной области, где ![]() , а в оставшихся областях функции
, а в оставшихся областях функции ![]() , по совокупности принимают значения разных знаков.
, по совокупности принимают значения разных знаков.
Для определенности будем считать
![]() (4)
(4)
Введем в рассмотрение линии уровня
![]()
и составим множества ![]() ,
,
Пусть выполняется условие
U4. Произвольные линии из множеств ![]() , а также из множеств
, а также из множеств ![]() пересекаются только в одной точке.
пересекаются только в одной точке.
Заметим, ![]() .
.
Далее рассмотрим линии уровня
![]() .
.
Линии ![]() согласно U.4 пересекаются только в одной точке (всего четыре точки). Функции
согласно U.4 пересекаются только в одной точке (всего четыре точки). Функции ![]() непрерывны
непрерывны ![]() , тогда точки пересечения линий
, тогда точки пересечения линий ![]() принадлежат достаточно малой окрестности точки
принадлежат достаточно малой окрестности точки ![]() . К примеру за это окрестность можно взять область, оганиченную линиями
. К примеру за это окрестность можно взять область, оганиченную линиями ![]() .
.
Область ограниченную ![]() обозначим
обозначим ![]() ;
; ![]() обозначим
обозначим ![]() ;
; ![]() обозначим
обозначим ![]() ;
; ![]() обозначим
обозначим ![]() .
.
Согласно U.1 линии уровня определяемые функциями ![]() являются аналитическими кривыми и их можно представить параметрически [6].
являются аналитическими кривыми и их можно представить параметрически [6].
Возьмём ![]() и её уравнение представим параметрически в виде
и её уравнение представим параметрически в виде ![]() (случай
(случай ![]() не исключается), где
не исключается), где ![]() означает длину дуги
означает длину дуги ![]() отсчитываемого от точки
отсчитываемого от точки ![]() .
.
Возьмем ![]() и ее уравнение представим в виде
и ее уравнение представим в виде
![]()
(случай ![]() не исключается), где
не исключается), где ![]() означает длину дуги
означает длину дуги ![]() отсчитываемого от точки
отсчитываемого от точки ![]() .
.
Также обозначим
![]()
Вспомогательные леммы
Лемма 1. Функция ![]() строго монотонна вдоль линии
строго монотонна вдоль линии ![]() , а функция
, а функция ![]() вдоль линии
вдоль линии ![]() .
.
Доказательство леммы приведен в [7].
Лемма 2. В каждом из частей ![]() .
.
Доказательство. Пусть ![]() . Возьмем
. Возьмем ![]() .
.
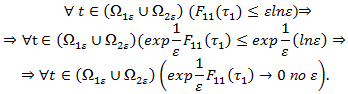
Отсюда следует справедливость леммы для одного случая. Оставщиеся случаи доказываются аналогично.
Решение задачи
Теорема. Пусть выполняются условия u.1-u.4. Тогда существует решение задачи (1) – (2) и ![]() являются областями притяжения для решений
являются областями притяжения для решений ![]() .
.
Доказательство. Для рассматриваемого случая решение задачи (1)-(2) можно представить в виде
![]()
где ![]() .
.
Функцию ![]() будем рассматривать для
будем рассматривать для ![]() . При исследовании
. При исследовании ![]() существенную роль играют знаки функций
существенную роль играют знаки функций ![]() и асимптотическое поведение интегралов
и асимптотическое поведение интегралов ![]() . Выберем пути интегрирования для этих интегралов. Путь для всех случаев
. Выберем пути интегрирования для этих интегралов. Путь для всех случаев ![]() выбирается единым и состоит из части
выбирается единым и состоит из части ![]() соединяющего точки
соединяющего точки ![]() соединяющего точки
соединяющего точки ![]() .
.
При j=1 получим путь ![]() .
.
Компоненты ![]() в зависимости от знака функций
в зависимости от знака функций ![]() представим в различных вариантах. Знаки
представим в различных вариантах. Знаки ![]() определяются согласно (4).
определяются согласно (4).
- Пусть
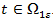 . Тогда
. Тогда 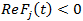 и компоненты
и компоненты 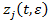 представляются в виде
представляются в виде
![]() (5)
(5)
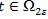 . В этом случае
. В этом случае 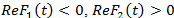 и
и
![]() (6)
(6)
![]() (7)
(7)
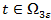 . Имеем
. Имеем 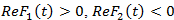 и
и
![]() (8)
(8)
![]() . (9)
. (9)
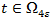 , тогда и
, тогда и
![]() (10)
(10)
С учетом выбранных путей интегрирования и параметрическое представление линий ![]() интегралы
интегралы ![]() представим в виде
представим в виде
![]()
где 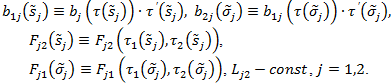
Во всех рассматриваемых случаях будут присутствовать интегралы
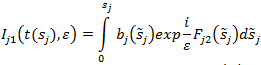
К таким интеграл применяя метод стационарной фазы (функция ![]() не имеет особенностей) [6] получим
не имеет особенностей) [6] получим
![]() (11)
(11)
Если ![]() , то к интегралу
, то к интегралу
![]()
применяя интегрирование по частям имеем
![]() (12)
(12)
Если ![]() то согласно (7)-(8)-(9)-(10) рассмотрим выражения
то согласно (7)-(8)-(9)-(10) рассмотрим выражения
![]()
которые можно записать так
![]() .
.
К ![]() применяя интегрирование по частям и учитывая Лемму 1 получим
применяя интегрирование по частям и учитывая Лемму 1 получим
![]() .
.
Заметим, что ![]() .
.
Теперь каждый из случаев ![]() рассмотрим отдельно. Отметим, что в каждом случае надо учесть Лемму 2.
рассмотрим отдельно. Отметим, что в каждом случае надо учесть Лемму 2.
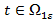 , тогда на основе (11), (12), (j=12) имеем
, тогда на основе (11), (12), (j=12) имеем
Так как ![]() то
то
![]()
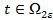 . В этом случае учитывая (11)-(12) при j=1 и (13) при j=2 будем иметь
. В этом случае учитывая (11)-(12) при j=1 и (13) при j=2 будем иметь
![]() .
.
- Если
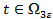 , то учтем (11), (12) при j=2 и (13) при j=1.
, то учтем (11), (12) при j=2 и (13) при j=1.
![]() .
.
- Пусть
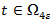 . Тогда надо учесть (11)-(12) при j=1,2, a (13) при j=1,2.
. Тогда надо учесть (11)-(12) при j=1,2, a (13) при j=1,2.
![]() . Теорема доказана.
. Теорема доказана.
Заключение
- Работа носит теоретический характер, но полученные результаты можно использовать на практике, когда состояние объекта описывается сингулярно возмущенными уравнениями (системами), причем объект при различных режимах стремится к определенному стабильному состоянию, а также при построении областей притяжения для систем сингулярно возмущенных уравнений более общего вида.
- Как показывают наши исследования, области притяжения, в некоторых случаях, существуют не для всех решений вырожденных уравнений (систем). Для подтверждения этого высказывания достаточно заменить
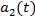 на
на 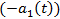 .
.
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Мищенко Е.Ф. Дифференциальные уравнения с малым параметром и релаксационные колебания / Е.Ф.Мищенко, Н.Х. Розов – М: Наука, 1975. - 248 с.
- Тихонов А.Н. Системы дифференциальных уравнений содержащие малые параметры при производных / А.Н.Тихонов // Мат.сб. – 1952.-Т.31(73), №3. – С. 575-586.
- Васильева А.Б. Асимптотические разложения решений сингулярно возмущенных уравнений / А.Б. Васильева, В.Ф. Бутузов // Москва: Наука, 1973. -278 с.
- Евграфов М.А. Асимптотика решений уравнения при в комплексной плоскости / М.А. Евграфов, М.В. Федорюк // Успехи математических наук, 21 -1966. – Т.21, №1, С. 3-50.
- Федорюк М.В. Асимптотика дискретного спектра оператора / М.В. Федорюк // Матем.сб., 68(110), 1965, №1, С. 68-97.
- Федорюк М.В. Топология линий Стокса уравнений второго порядка / М.В.Федорюк // Изв. АН СССР. -Сер.матем, 29(1965), В. 3, С. 645-656.
- Федорюк М.В. Метод перевала / М.В.Федорюк // Москва: Наука, 1977, С. 368.
- Алыбаев К.С. Метод линий уровня исследования сингулярно возмущенных уравнений при нарушении условия устойчивости / К.С. Алыбаев // Вестник КГНУ. – Серия 3, Выпуск 6. – Бишкек, 2001. – С. 190-200.
- Алыбаев К.С. Метод погранслойных линий построения регулярно и сингулярных областей для линейных сингулярно возмущенных уравнений с аналитическими функциями / К.С.Алыбаев, К.Б. Тампагаров // Естественные и математические науки в современном мире: сб. статей по материалам XLVIIмеждународной научно-практической конференции. № 10 (45) Россия, Новосибирск: СиБАК, 2016. – С. 59-66.
- Тампагаров К.Б. Погранслойные линии для сингулярно и регулярно возмущенных дифференциальных уравнений первого порядка с аналитическими функциями / К.Б. Тампагаров // Естественные и математические науки в современном мире: сб. статей по материалам XLVII международной научно-практической конференции. №10 (45). Россия, Новосибирск: СиБАК, 2016. – С. 67-73.
- Olver W.J Error bounds for the Liouville - Green (or WKB) approximation /J.Olver. // ProcCambridge Phil.Soc., 57-1966. – T.57. - Р. 790-810.
- Heading J. The stokes phenomenon and certain nth order differential equations,I,II / Heading // Proc. CambridgePhil.Soc.,53(1957) - Р. 399-441.
Список литературы на английском языке / References in English
- Mishchenko E.F. Differentsial'nyye uravneniya s malym parametrom i relaksatsionnyye kolebaniya [Differential Equations with Small Parameter and Relaxation Oscillations] / E.F. Mishchenko, N.Kh. Rozov - M: Science, 1975, – 248 p. [in Russian]
- Tikhonov A.N. Sistemy differentsial'nykh uravneniy soderzhashchiye malyye parametry pri proizvodnykh [Systems of Differential Equations Containing Small Parameters for Derivatives] / A.N. Tikhonov // Math. Col. – 1952. – V.31 (73), No.3. – P. 575-586. [in Russian]
- Vasilyeva A.B. Asimptotika resheniy uravneniya pri v kompleksnoy ploskostiz [Asymptotic Expansions of Solutions of Singularly Perturbed Equations] / AB. Vasilyeva, V.F. Butuzov // Moscow: Nauka, 1973 – 278 p. [in Russian]
- Evgrafov M.A. Asimptotika resheniy uravneniya pri v kompleksnoy ploskostiz [Asymptotics of Solutions of Equation in Complex Plane] / M.A. Evgrafov, M.V. Fedoruk // Uspekhi Matematicheskikh Nauk [Successes of Mathematical Sciences], 21 – 1966. – V.21, No.1 – P. 3-50. [in Russian]
- Fedoryuk M.V. Asimptotika diskretnogo spektra operatora [Asymptotics of Discrete Spectrum of Operator] / M.V. Fedoryuk // Math. Sc., 68 (110), 1965, No. 1 – P. 68-97. [in Russian]
- Fedoryuk M.V. Topologiya liniy Stoksa uravneniy vtorogo poryadka [Topology of Stokes lines of second-order equations] / M.V. Fedoryuk // Izv. AN SSSR. – Math.Ser., 29 (1965), B. – P. 645-656. [in Russian]
- Fedoryuk M.V. Metod perevala [Saddle-point method] / M.V. Fedoryuk / Moscow: Science, 1977 – P. 368. [in Russian]
- Alibayev K.S. Metod liniy urovnya issledovaniya singulyarno vozmushchennykh uravneniy pri narushenii usloviya ustoychivosti [Method of Level Lines for Investigating Singularly Perturbed Equations under Violation of Stability Condition] / К.S. Alybaev // Vestnik KGNU [Bulletin of KSNU]. – Series 3, Issue 6. – Bishkek, 2001. – P. 190-200. [in Russian]
- Alibayev K.S. Metod pogransloynykh liniy postroyeniya regulyarno i singulyarnykh oblastey dlya lineynykh singulyarno vozmushchennykh uravneniy s analiticheskimi funktsiyami [Method of Boundary Layer Lines for Construction of Regular and Singular Domains for Linear Singularly Perturbed Equations with Analytic Functions] / K.S.Alibaev, K.B. Tampagarov // Yestestvennyye i matematicheskiye nauki v sovremennom mire: sb. statey po materialam XLVII mezhdunarodnoy nauchno-prakticheskoy konferentsii [Natural and mathematical sciences in the modern world: Sat. articles on the materials of the XLVII International scientific and practical conference]. № 10 (45) Russia, Novosibirsk: SIBAK, 2016. – P. 59-66 [in Russian]
- Tampagarov K.B. Pogransloynyye linii dlya singulyarno i regulyarno vozmushchennykh differentsial'nykh uravneniy pervogo poryadka s analiticheskimi funktsiyami [Boundary Lines for Singularly and Regularly Perturbed First-Order Differential Equations with Analytic Functions] / К.B. Tampagarov // Yestestvennyye i matematicheskiye nauki v sovremennom mire: sb. statey po materialam XLVII mezhdunarodnoy nauchno-prakticheskoy konferentsii [Natural and mathematical sciences in the modern world: Sat. articles on the materials of the XLVII International scientific and practical conference]. №10 (45). Russia, Novosibirsk: SIBAK, 2016. – P. 67-73 [in Russian]
- Olver W.J Error bounds for the Liouville - Green (or WKB) approximation /J.Olver. // Proc. Cambridge Phil. Soc., 57-1966. – T.57. – Р. 790-810.
- Heading J. The stokes phenomenon and certain nth order differential equations, I, II / Heading // Proc. Cambridge Phil. Soc., 53(1957) – Р. 399-441.
