МОДЕЛИРОВАНИЕ НАГРЕВА КВАРЦЕВЫХ ТРУБ ПОДВИЖНЫМ ИСТОЧНИКОМ ВОЗДЕЙСТВИЯ ДЛЯ РЕШЕНИЯ ЗАДАЧИ УПРАВЛЕНИЯ ПРОЦЕССОМ MCVD
Первадчук В.П.1, Владимирова Д.Б.2, Дектярев Д.Н.3, Пестерев А.А.4
1Доктор технических наук, профессор, ФГБОУ ВПО Пермский национальный исследовательский политехнический университет, 2Кандидат физ.-мат. наук, доцент, ФГБОУ ВПО Пермский национальный исследовательский политехнический университет, 3Аспирант, ФГБОУ ВПО Пермский национальный исследовательский политехнический университет, 4Аспирант, АО Пермская научно-производственная приборостроительная компания
МОДЕЛИРОВАНИЕ НАГРЕВА КВАРЦЕВЫХ ТРУБ ПОДВИЖНЫМ ИСТОЧНИКОМ ВОЗДЕЙСТВИЯ ДЛЯ РЕШЕНИЯ ЗАДАЧИ УПРАВЛЕНИЯ ПРОЦЕССОМ MCVD
Аннотация
В настоящей работе построена математическая модель нагрева кварцевой трубы подвижным тепловым источником, которая описывает температурное поле в кварцевой трубе, формируемое в ходе реального технологического процесса. Математическая модель включает в себя уравнение теплопроводности и модель подвижного источника, т.е. описание формы и мощности подводимого теплового потока, а также закон движения источника. Результаты математического описания сопоставлены с результатами натурных экспериментов, установлены зависимости между параметрами модели и параметрами эксперимента.
Ключевые слова: оптимальное управление, подвижный тепловой источник, MCVD процесс.Pervadchuk V.P.1, Vladimirova D.B.2, Dektyarev D.N.3, Pesterev A.A.4
1PhD in Engineering, Perm National Research Polytechnic University, 2PhD in Physics and Mathematics, Perm National Research Polytechnic University, 3Postgraduate student, Perm National Research Polytechnic University, 4Postgraduate student, Perm Scientific-Industrial Instrument Making Company
SIMULATION OF HEATING QUARTZ TUBES BY MOVING HEAT SOURCE FOR SOLVING PROBLEM OF PROCESS CONTROL MVCD
Abstract
In this work the mathematical model of heating of a quartz tube is constructed by a moving heat source which describes the temperature field in a quartz tube formed during real technological process. The mathematical model includes heat equation and the model of the moving heat source, i.e. description of the shape and power of heat flow and the law of motion of the source. The results have been compared with field experiments, model parameters have been correlated with the experiment parameters.
Keywords: optimal control, moving heat source, MCVD process.Введение
Технологические процессы, характеризующиеся наличием подвижных источников воздействия (тепловых, электромагнитных и т.д.) описан классом систем с подвижным управлением. В работах Бутковского А.Г. и Пустыльникова Л.М. [1, 2] впервые рассмотрены вопросы подвижного управления тепловыми процессами, выполнены теоретические постановки различных практических задач, приведены примеры. В литературе можно найти работы зарубежных авторов [3, 4], посвящённых исследованию проблем управления в системах с подвижным источником воздействия.
В работе [5] авторы ставят и решают задачу моделирования и реализации системы управления подвижным источником энергии (электронным лучом, генерируемым электронной пушкой) при выплавке слитков в плоском кристаллизаторе. Задачей управления является обеспечение и поддержание заданного температурного поля на поверхности слитка путём выработки управляющих воздействий: мощности электронного луча и траектории (закона) его движения, при наличии внешних возмущений.
Одним из ключевых этапов производства специальных волоконных световодов является изготовления преформ методом модифицированного парофазного осаждения (далее процесс MCVD). Технологический процесс MCVD заключается в следующем (Рис. 1). В опорную кварцевую трубку подают пары легирующих компонентов(SiCl4, GeCl4, BCl3, POCl3 и т.д.) и очищенный кислород. В зоне нагрева трубки кислородно-водородной горелкой, перемещающейся вдоль трубки с заданной скоростью, происходит окисление легирующих компонентов с образованием оксидов, часть из которых под действием сил термофореза осаждается в виде тонкого слоя на внутренней поверхности кварцевой трубы [6]. Подбирая параметры этого технологического процесса можно получить требуемую концентрацию легирующих элементов, а значит и соответствующий коэффициент преломления света.
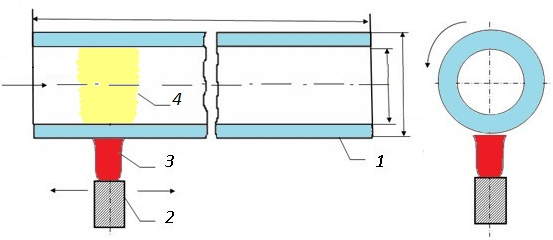
Рис.1 - Схематическое изображение процесса MCVD: 1 – кварцевая труба; 2 – движущаяся горелка (стрелки показывают направление движения); 3 – пламя горелки; 4 - зона реакции
Одной из важнейших практических задач при реализации процесса MCVD является обеспечение однородности оптических и геометрических параметров изготавливаемой заготовки по длине. Для решения этой задачи требуется точная настройка системы управления параметрами процесса, в первую очередь, скоростью движения горелки и температурой в зоне протекания химических реакций, образования оксидов и осаждения оксидов на стенки опорной трубы.
Суть проблемы заключается в том, что контролировать температуру непосредственно в зоне реакции, где протекают физико-химические процессы, затруднительно. В то же время распределение температурного поля в зоне образования окислов определяет не только размеры и концентрацию коагулированных частиц, но направление их движения под действием сил термофореза, так как термофоретическая сила, действующая на каждую частицу пропорциональна градиенту температурного поля в данной точке [7]. На практике ведения MCVD процесса контролируют температуру на поверхности кварцевой трубы с помощью бесконтактных инфракрасных пирометров.
Постановка задачи.
В процессе MCVD для обеспечения равномерности толщины осаждённого слоя скорость движения горелки вдоль кварцевой трубы изменяется. Как правило, постепенно увеличивается от начала к концу прохода. При увеличении скорости движения подвижного источника изменяется температурное поле как в кварцевой трубе, так и в движущейся газовой смеси.
Построим математическую модель нагрева кварцевой трубы подвижным тепловым источником, которая с достаточной точностью опишет температурное поле в кварцевой трубе, формируемое в ходе реального технологического процесса.
Математическая модель включает в себя уравнение энергии, в нашем случае уравнение теплопроводности, и модель подвижного источника, т. е. описание формы и мощности подводимого теплового потока, а также закон движения источника.
Подвижный источник нагрева - тепловой поток q(z,t) от газовой горелки опишем функцией Гаусса, имеющей вид
 (1)
(1)
где u(ξ) – скорость движения горелки, H – дисперсия (ширина пламени горелки), qmax – мощность горелки, t – время, z – пространственная переменная.
Уравнение теплопроводности получено при следующих предположениях:
-температурное поле кварцевой трубки осесимметричное (это обеспечивается вращением трубы);
-теплообмен с внешней окружающей средой и газом, текущим в внутри трубы, описывается законом Ньютона;
-излучение с внешней поверхности трубы подчиняется закону Стефана-Больцмана.
Тогда в цилиндрической системе координат уравнение теплопроводности запишется в виде:
![]() (2)
(2)
где T(t,r,z,) - температура кварца; t–время; K, Cp, λ- плотность, удельная теплоемкость и теплопроводность кварца соответственно; r,z–пространственные переменные.
Уравнение (2) дополним начальным и граничными условиями вида:
![]() (3)
(3)
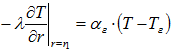 (4)
(4)
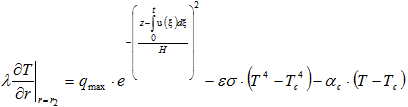 (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
Расчетно-экспериментальное определение параметров модели подвижного источника воздействия.
Как отмечено выше, для идентификации подвижного теплового источника нужно определить функцию мощности qmax и параметр формы Н, которые являются характеристиками конкретного источника и должны определятся из эксперимента (см. ниже). Закон движения источника, т.е.изменение скорости u(t) со временем может быть известно заранее.
Если горелка неподвижна u(t)=0, то необходимо подобрать только две функции - qmax и H. Для их определения нужно провести серию экспериментов по нагреву кварцевых труб пламенем горелки и замеру с помощью сканирующего пирометра через фиксированные промежутки времени распределение температуры на внешней поверхности трубы. По полученной информации можно подобрать искомые величины qmax и H таким образом, что при их подстановке в уравнение (2), из решения последнего получали бы распределение температуры на внешней поверхности трубы, совпадающие с экспериментально полученными значениями.
На рис. 2 представлены экспериментальные и расчетные данные (с подобранными параметрами qmax и H) по распределению температуры на внешней поверхности трубы при неподвижной горелке.
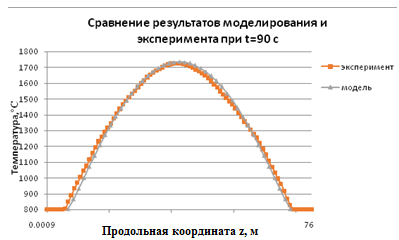
Рис. 2 - Сравнение результатов численного моделирования и эксперимента при неподвижном тепловом источнике
Очевидно, что по мере увеличения расхода водородно-кислородной смеси будут также увеличиваться значения параметров qmax и H. Проведенные эксперименты показали, что в исследованном диапазоне параметры qmax и H линейно зависят от расхода водорода (рис. 3 и 4, а также формулы (8) и (9))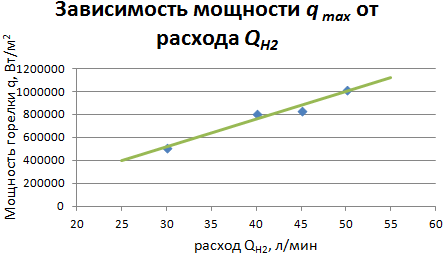
Рис. 3 - Зависимость параметра мощности qmax от расхода водорода QH2
qmax = 24099 * QH2 - 206252 (8)
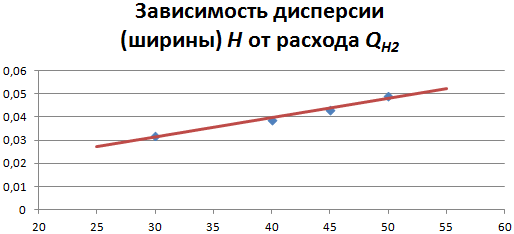
Рис. 4 - Зависимость дисперсии H от расхода водорода QH2
Н = 0,000829 * QH2 + 0,006572 (9) Из двух последних уравнений легко найти зависимость между qmax и H: qmax = 2,907*10+7 * H - 15192 (10) H = 3,44*10-8 * qmax + 0,000523 (11)Основные результаты и их обсуждения.
После определения параметров подвижного источника qmax и H численно и экспериментально было исследовано влияние различных факторов на температурное поле кварцевой трубы, и в первую очередь, на распределение температуры на внешней поверхности трубы и на максимальное значение этой температуры Tmax. Отметим, что в большинстве случаев контроль и управление тепловым состоянием процесса MCVD осуществляются с помощью максимальной температуры. С точки зрения практики к числу таких факторов, оказывающих существенное влияние на температурное поле трубы, относятся скорость движения горелки u(ξ) и расход водорода QH2.
Для натурного эксперимента использовали трубу из синтетического кварца с внешним диаметром d2=28мм, внутренним диаметром d1=24мм и длиной L=500мм, скорость вращения трубы вокруг своей оси была постоянна и равнялась 30 об/мин, расходы газа внутри трубы: кислород – 1,2 л/мин, гелий – 1,2 л/мин, расход газа азота, идущего на обдув пламени, был равен 2 л/мин., скорость движения горелки варьировали от 70 до 130 мм/мин с шагом 20 мм/мин, при этом максимальная температурана поверхности кварцевой трубы не выходила из диапазона 1800±5ᵒС. Температуру поверхности кварцевой трубы измеряли с помощью сканирующего пирометра Raytek F5ETMP150G5R1; полученную температуру записывали в файл для последующей обработки и анализа.
Численные расчеты модели проводились с помощью программных пакетов COMSOLMultiphysics и MatLab. На рис. 5-8 изображены расчетное температурное поле Tm(z,t) и температурное поле, полученное из натурного эксперимента Te(z,t) при скоростях движения горелки 70, 90, 110 и 130 мм/мин
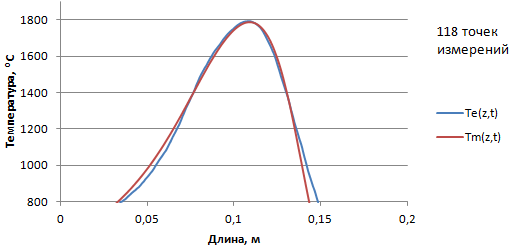
Рис.5 - Сравнение результатов моделирования Tm(z,t) и эксперимента Te(z,t), скорость движения горелки = 70 мм/мин
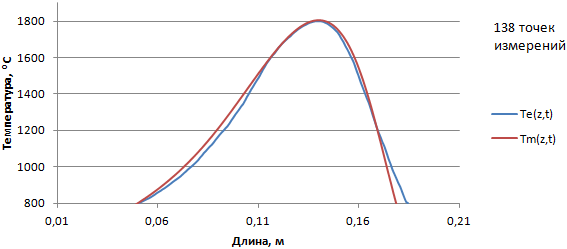
Рис.6 - Сравнение результатов моделирования Tm(z,t) и эксперимента Te(z,t), скорость движения горелки = 90 мм/мин
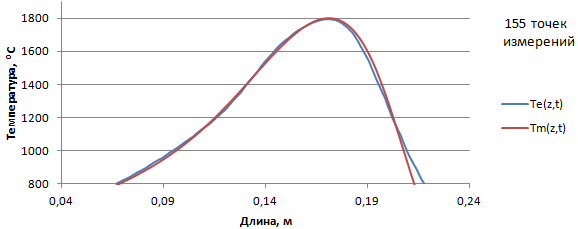
Рис.7 - Сравнение результатов моделирования Tm(z,t) и эксперимента Te(z,t), скорость движения горелки = 110 мм/мин
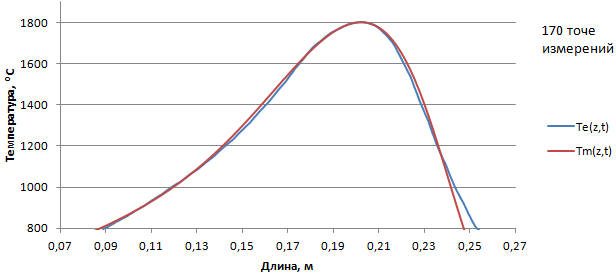
Рис.8 - Сравнение результатов моделирования Tm(z,t) и эксперимента Te(z,t), скорость движения горелки = 130 мм/мин
Оценку точности соответствия результатов моделирования результатам эксперимента выполним путем вычитания массива расчетных данных из массива эксперимента. Для каждой скорости движения горелки, в диапазоне температур от 1500 до 1800ᵒС, полученная разница укладывается в диапазон точности измерения сканирующего пирометра: ±0,5% от измеренной величины. Это подтверждает, что математическая модель с достаточной точностью имитирует реальное температурное поле кварцевой трубы.
Теоретические и экспериментальные исследования позволили не только количественно оценить влияние различных факторов на тепловые процессы (см. рис.5-8), но и получить ряд важных закономерностей, представляющих определенный практический интерес для технологии MCVD. Здесь имеется в виду, тот факт, что при неподвижной горелке максимальная температура кварцевой трубы находится на оси симметрии факела пламени. Однако по мере увеличения скорости горелки максимальная температура начинает смещаться от оси симметрии в сторону противоположную направления движения горелки. Причем, чем больше скорость теплового источника, тем больше смещение. Указанный факт необходимо принимать во внимание при контроле и управлении процессом с помощью ИК-пирометров.
Заключение
Работы в направлении повышения качества геометрических и оптических характеристик заготовок изготовленных методом MCVD возможны путём усовершенствования технологических процессов.
Полученные результаты моделирования подвижного источника соответствуют результатам натурного эксперимента нагрева кварцевой трубы с достаточным уровнем точности и могут быть использованы в дальнейшем для построения распределенных систем управления с подвижным источником воздействия.
Литература
- Бутковский А.Г., Даринский Ю.В., Пустыльников Л.М. Управление распеделенными системами путем перемещения источника. Автоматика и телемеханика, 1974, №5.
- Бутковский А.Г., Пустыльников Л.М. Теория подвижного управления системами с распределенными параметрами. М.: "Наука", 1980.
- Martin J.-C.E. On an Optimal Scanning Control Problem in an One Dimensional Space. IEEE Trans on Autom. Contr., 1977, Vol.AC-22, №4, p.905-915.
- Martin J.-C.E. Chryssoverghi J.N. Optimal Boundary Scanning Control of Parabolic Systems Using Relaxed Controls. J. of Contr., 1978, Vol.27, №6, p.905-915.
- В.А. Кубышкин, В.С. Суховеров. Система моделирования и управления подвижным воздействием на базе программных средств MATLAB. Проблемы управления №2, 2008.
- MacChesney and Kenneth l. Walker. An overview of the Modified Chemical Vapor Deposition (MCVD) process and performance. IEEE JOURNAL OF QUANTUM ELECTRONICS, VOL. QE-18, NO. 4, APRIL
- L. WALKER, F. T. GEYLING, and S. R. NAGEL. Thermophoretic Deposition of Small Particles in the Modified. Thermophoretic Deposition of Small Particles in the Modified. Journal of the American Ceramic Society. 1980.
References
- Butkovskij A.G., Darinskij Ju.V., Pustyl'nikov L.M. Upravlenie raspedelennymi sistemami putem peremeshhenija istochnika. Avtomatika i telemehanika, 1974, №5..
- Butkovskij A.G., Pustyl'nikov L.M. Teorija podvizhnogo upravlenija sistemami s raspredelennymi parametrami. : "Nauka", 1980.
- Martin J.-C.E. On an Optimal Scanning Control Problem in an One Dimensional Space. IEEE Trans on Autom. Contr., 1977, Vol.AC-22, №4, p.905-915.
- Martin J.-C.E. Chryssoverghi J.N. Optimal Boundary Scanning Control of Parabolic Systems Using Relaxed Controls. Int. J. of Contr., 1978, Vol.27, №6, p.905-915.
- A. Kubyshkin, V.S. Suhoverov. Sistema modelirovanija i upravlenija podvizhnym vozdejstviem na baze programmnyh sredstv MATLAB. Problemy upravlenija №2, 2008.
- MacChesney and Kenneth l. Walker. An overview of the Modified Chemical Vapor Deposition (MCVD) process and performance. IEEE JOURNAL OF QUANTUM ELECTRONICS, VOL. QE-18, NO. 4, APRIL
- L. WALKER, F. T. GEYLING, and S. R. NAGEL. Thermophoretic Deposition of Small Particles in the Modified. Thermophoretic Deposition of Small Particles in the Modified. Journal of the American Ceramic Society. 1980.
