ГРАВИТАЦИОННОЕ ПРИТЯЖЕНИЕ К ЦЕНТРУ ПОЛОСТИ ШАРОВОГО СЛОЯ ВЕЩЕСТВА

Гневко А.И.¹, Соловов С.Н.², Янушкевич В.А.³

¹ доктор технических наук, профессор, ВА РВСН им. Петра Великого; ² кандидат технических наук, доцент, ВА РВСН им. Петра Великого; ³ доктор физико-математических наук, профессор, ВА РВСН им. Петра Великого.

ГРАВИТАЦИОННОЕ ПРИТЯЖЕНИЕ К ЦЕНТРУ ПОЛОСТИ ШАРОВОГО СЛОЯ ВЕЩЕСТВА

Аннотация

На основе модели сжатого вакуума, подобного твёрдому телу, предложено объяснение высоких скоростей звёзд в центральных областях галактик. Отличие от известных представлений заключается в преобладании гравитации, возникающей за счёт усиления продольных волн в вакууме при прохождении через микрочастицы вещества большого шарового слоя. Образуются лучи, подобные лазерным. Количество лучей, проходящих через точку, определяет центростремительные силы в шаровой полости.

Ключевые слова: Гравитация, шаровый слой вещества, галактика, сжатый вакуум, твердотельная модель.

Gnevko, A.I.¹, Solovov S.N.², Yanushkevich V.A.³

¹ PhD in Engineering, professor, Peter the Great Strategic Missile Troops Academy; ² PhD in Engineering, assosiate professor, Peter the Great Strategic Missile Troops Academy; ³ PhD in Physics and Mathematics, professor, Peter the Great Strategic Missile Troops Academy.

GRAVITATIONAL ATTRACTION TO THE CENTER OF CAVITY OF SPHERICAL LAYER OF SUBSTANCE

Abstract

Explanation of high velocities of stars in central regions of galaxies is suggested on the basis of model of squeezed vacuum, similar to solid body. The difference from known perceptions lies in predominance of gravitation occurring due to strengthening of longitudinal waves in vacuum when passing through micro-particles of a substance of a big spherical layer. Beams, similar to laser, are generated. The number of beams passing through the point determines circular force in the spherical cavity.

Keywords: Gravitation, spherical layer of substance, galaxy, squeezed vacuum, solid body model.

Известно, что в соответствии с законами Ньютона внутри полого шарового слоя, состоящего из рассеянного вещества, сумма гравитационных сил равна нулю. Вместе с тем, результаты наблюдений за ядрами галактик и образованием звёзд, имеющих планетные системы, дают основания предполагать существование центростремительных сил внутри таких полостей. Одной из важных особенностей наблюдений за ядрами галактик является высокая скорость движения звёзд около некоторого центра, что позволяет предполагать существование в этих центрах чёрных дыр. Причем скорость звёзд тем выше, чем крупнее галактика. Природа высоких скоростей звёзд в центрах галактик может быть объяснена с помощью модели МСВ (модель сжатого вакуума) [1].

Отличительной особенностью модели МСВ является предположение о том, что продольные упругие волны, распространяющиеся в физическом вакууме, усиливаются при прохождении микрочастиц вещества. Физический вакуум сжат, что обеспечивает необходимую энергию для усиления. Усиление приводит к тому, что при расположении микрочастиц в ряд вдоль распространения продольной волны реализуется некоторое подобие лазера. Луч продольных волн расходится с увеличением расстояния меньше, чем в случае хаотичного расположения микрочастиц (рис. 1).

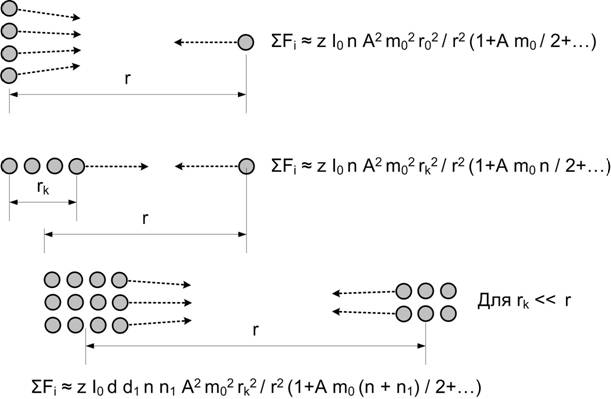
Рис.1. Гравитационное взаимодействие нуклонов при основных видах их расположения.

I_o – интенсивность продольных волн, Н;

z – параметр, учитывающий пространственное распределение излучения;

d, d₁ – количество рядов во взаимодействующих телах;

n, n₁ – количество нуклонов в рядах;

А – коэффициент усиления продольных волн, кг^-1;

m₀ – масса нуклона, кг;

r – расстояние между взаимодействующими телами;

r₀ – радиус нуклона, м;

r_k – длина рядов, м;

∑F_i – сила гравитационного взаимодействия тел, Н.

Кроме того, усиление волн при прохождении вдоль ряда микрочастиц больше, чем усиление при хаотичном расположении частиц. Поэтому с увеличением длины рядов гравитация начинает определяться числом нуклонов в ряду, длиной и количеством рядов, проходящих через данную точку пространства. По современным представлениям основная масса видимого вещества в нашей Вселенной сосредоточена в настоящее время в виде нейтронов и протонов (нуклонов). Попытки связать тёмную материю с микрочастицами пока безуспешны. Размеры нуклонов определяют число и распределение возможных рядов, а, следовательно, и распределение гравитационных сил в пространстве (рис. 2). Согласно МСВ, с ростом плотности рядов, гравитационные силы, определяемые рядами, начинают существенно превосходить силы гравитации по Ньютону. В соответствии с моделью Ньютона силы гравитации определяются простым суммированием гравитационного действия каждой из микрочастиц вещества. Силы аддитивны и не учитывают дополнительного усиления продольных волн при прохождении через вещество. Следует отметить, что ОТО (общая теория относительности Эйнштейна), как и МСВ считает гравитационные силы, отличающимися от сил Ньютона [3].

Если размеры (толщина) шарового слоя существенно превосходят размеры шаровой полости, то расстояния внутри полости, согласно МСВ, практически не влияют на величину гравитационных сил, определяемых длиной и концентрацией массы в рядах. В то же время при перемещении от центра полости к её границе возникает центростремительная сила гравитации в связи с увеличением области S_B > S_A шарового слоя, притягивающей к центру (рис. 2). При этом сила в центре полости равна нулю, как и сила Ньютона, а внутри полости гравитационная сила растёт по мере удаления от центра. Но, согласно Ньютону, увеличение области шарового слоя, притягивающей к центру, компенсируется увеличением расстояния от точки полости до притягивающей к центру массы.

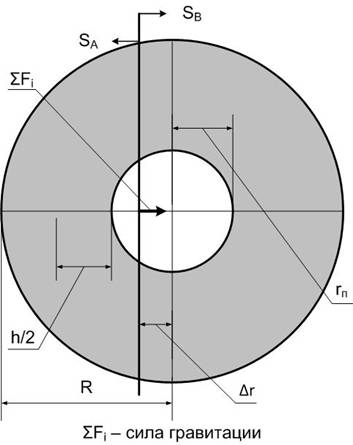
Рис. 2. Схема шарового слоя с внутренней полостью.

В отличие от модели Ньютона по МСВ компенсация с расстоянием может быть существенно меньше с увеличением толщины шарового слоя. С ростом толщины шарового слоя проявляется аддитивность гравитации по Ньютону. Вместе с тем, с ростом толщины шарового слоя по МСВ должно наблюдаться действие дополнительных гравитационных сил, вызванное усилением продольных волн при прохождении вещества. Естественно, что по мере увеличения толщины шарового слоя, согласно МСВ, растёт и величина центростремительной силы внутри полости, в отличие от отсутствия гравитационных сил внутри полости по Ньютону.

Для гравитации по Ньютону внутри тонкого шарового слоя при удалении от центра на расстоянии ∆r силы, направленные от центра и к центру, за счет изменения площади поверхности относятся как (r_п – ∆r)² ∕ (r_п + ∆r)², где r_п – радиус полости. В тоже время силы, направленные от центра и к центру, за счёт приближения к массам на границе слоя и удаления на противоположной стороне относятся как (r_п + ∆r)² / (r_п – ∆r)². Таким образом, влияние на гравитационные силы изменения площади поверхности компенсируется влиянием изменения расстояния. Поэтому в любой точке полости гравитационные силы, направленные к центру и от центра, равны и их сумма равна нулю для тонкого шарового слоя. Но шаровый слой любой толщины можно представить как сумму тонких шаровых слоёв. По Ньютону гравитационное действие тонких шаровых слоёв определяется простым суммированием. Поэтому в полости шарового слоя любой толщины сумма гравитационных сил равна нулю.

Для гравитации по МСВ преобладающую роль играют ряды, а не отдельные нуклоны. Поэтому для шарового слоя большой величины равенство нулю суммы гравитационных сил в полости нарушается. Преобладают центростремительные силы. Соотношение между силами за счёт изменения площади поверхности сохраняется. Но соотношение между силами за счёт изменения расстояния иное (r_р/2 + ∆r)² / (r_р/2 – ∆r)², где r_р – длина ряда, которая равна толщине шарового слоя h (приблизительно равна радиусу шара R). r_р/2 соответствует средней длине всех возможных рядов, которые могут быть образованы в пределах всего ряда (по аналогии с лазером). Поскольку для шарового слоя большой толщины r_р/2 >> r_п > ∆r, отношение (r_р/2 + ∆r)² / (r_р/2 – ∆r)² приближённо равно единице (отличие может быть сколь угодно малым с ростом размеров шара) и внутри полости действуют центростремительные гравитационные силы. Так как (r_п – ∆r)² ∕ (r_п + ∆r)² меньше единицы, центростремительные силы больше, чем центробежные, если ∆r больше нуля.

Рассмотрение интенсивности продольных волн даёт основания считать, что в центре полости фон максимален. При рассмотрении учитывались все возможные расположения лучей. В соответствии с максимумом фона продольных волн двигающиеся вещественные объекты приобретают с течением времени максимальные приращения скорости (ускорения) [1]. Ускорения тем больше, чем ближе к центру полости расположено двигающееся тело и больше масса шарового слоя.

Представляет интерес, что постоянная гравитационного взаимодействия в связи с ростом фона продольных волн внутри полости также должна возрастать.  Поэтому возрастает и скорость движения звёзд в районе центральных частей галактик.

При движении вещества часть микрочастиц в ходе столкновений приобретает нулевую скорость, превращая энергию движения в энергию электромагнитного излучения и нагрев. Поэтому в центре полости скапливаются некоторые количества относительно неподвижного вещества. Высокая интенсивность продольных волн в центре полости приводит к относительному росту гравитационных сил, что приводит к формированию сверхмасс (чёрных дыр) в центрах галактик [1].

Отмеченный процесс характерен для формирования звезд и планетных систем из туманностей не только в центрах галактик, но и в других полостях, располагающихся в галактиках, например солнечной системы. Согласуется с отмеченными представлениями явление ускоренного звездообразования при столкновениях галактик [2].

Литература

1. Гневко А. И. О моделировании гравитации и некоторых явлений с нераскрытой природой. Возможности объединенного представления классической механики, релятивизма, квантования на основе аналогий в поведении физического вакуума и вязкоупругого твердого тела. – М.: Компания Спутник +, 2007. 77 с.
2. Ерошенко Ю. Н. Столкновение галактик. “Новости физики в сети Internet (по материалам электронных препринтов)”, УФН, том 172, номер 6 (2002), 700, URL: http://ufn.ru/ru/articles/2002/6/e/ (дата обращения 20.07.2016).
3. Зельманов А. Л., Агаков В. Г. Элементы общей теории относительности. – М.: Наука, Глав. Ред. физ-мат. лит., 1989. – 240 с.

 References

1. Gnevko A. I. O modelirovanii gravitacii i nekotoryh javlenij s neraskrytoj prirodoj. Vozmozhnosti ob#edinennogo predstavlenija klassicheskoj mehaniki, reljativizma, kvantovanija na osnove analogij v povedenii fizicheskogo vakuuma i vjazkouprugogo tverdogo tela [Modeling of gravity and some phenomena with untapped nature. The possibility of the unified presentation of classical mechanics, relativity, quantization on the basis of analogies in the behavior of the physical vacuum and viscoelastic solids]. – M.: Kompanija Sputnik +, 2007. 77 s. [in Russian]
2. Eroshenko Ju. N. Stolknovenie galaktik. “Novosti fiziki v seti Internet (po materialam jelektronnyh preprintov)” [The collision of galaxies. “Physics news on the Internet (based on electronic preprints)”], UFN, tom 172, nomer 6 (2002), 700, URL: http://ufn.ru/ru/articles/2002/6/e/ (data obrashhenija 20.07.2016). [in Russian]
3. Zel'manov A. L., Agakov V. G. Jelementy obshhej teorii otnositel'nosti [Elements of the General theory of relativity]. – M.: Nauka, Glav. Red. fiz-mat. lit., 1989. – 240 s. [in Russian]