ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ КОНИЧЕСКОЙ ДИФРАКЦИИ ДЛЯ РЕШЕТОК, РАБОТАЮЩИХ НА ПРОПУСКАНИЕ

Сагателян Г.Р.¹, Данилов Г.Ю.²

¹Доктор технических наук, профессор, ²Бакалавр, ФГБОУ ВО «Московский государственный технический университет имени Н.Э. Баумана (национальный исследовательский университет)»

ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ КОНИЧЕСКОЙ ДИФРАКЦИИ ДЛЯ РЕШЕТОК, РАБОТАЮЩИХ НА ПРОПУСКАНИЕ 

 Аннотация

В статье описана методика экспериментального определения углов дифракции в нулевом и первом порядках при косом наклонном падении света на амплитудные и рельефно-фазовые дифракционные решетки (ДР), работающие на пропускание, в отличие от известных аналогичных исследований, где рассматриваются только отражающие дифракционные решетки. Дано описание сконструированного для этой цели оптического стенда и специально изготовленных образцов, представляющих собой наборы амплитудных и рельефно-фазовых решеток разного периода. Приведена эмпирически установленная формула, описывающая взаимосвязь между углом поворота ДР и углом отклонения луча, дифрагированного на повернутой ДР. Установлена зависимость дифракционной эффективности от периода и глубины рельефа дифракционных решеток.

Ключевые слова: наклонное падение света; рельефно-фазовые дифракционные решетки; углы дифракции; дифракционная эффективность.

Sagatelyan H.R.¹, Danilov G.Ju.²

¹PhD in Engineering, Professor, ²Bachelor, Federal state budgetary institution of higher professional education Bauman Moscow State Technical University (National research university of technology)

EXPERIMENTAL DETERMINATION OF THE PARAMETERS OF CONICAL DIFFRACTION BY TRANSMISSION GRATINGS

Abstract

The article describes a method of experimental determination of the diffraction angles in the zero and first orders at oblique incidence of light on the amplitude and the relief-phase diffraction gratings (DG), working on the transmission, in contrast to the known similar studies, which deals only reflective diffraction gratings. The description of designed for this purpose optical bench and specially prepared samples, sets of amplitude and relief- phase gratings with different periods, is given. Empirical equation describing the relationship between the angle of rotation DG and the angle of deflection of the beam diffracted on a rotated DG is shown. The relationship between the diffraction efficiency, period and depth of the grooves is determined by experiment.

Keywords: oblique incident beam; relief-phase diffraction gratings; diffraction angles; diffraction efficiency. Введение

Известно, что при непараксиальной плоской дифракции неравномерность нарастания углов порядков дифрагированных лучей сильно зависит от угла падения пучка света на дифракционную решетку [1, 2]. Вместе с тем, при косом наклонном падении (коническая дифракция) возникают сложности математического описания углов распространения различных порядков дифрагированных лучей [3]. Наклонное падение света заключается в неперпендикулярности падающего луча плоскости ДР, косое наклонное падение – в  неперпендикулярности плоскости падения линиям ДР. Для аналитического описания углов распространения дифрагированных лучей при конической дифракции применяют метод, основанный на рассмотрении пространства направляющих косинусов [4].

Судя по результатам опубликованных исследований по применению конической дифракции в оптических и оптико-электронных приборах, рассматриваются исключительно дифракционные решетки, работающие на отражение [5 - 8]. В тех же случаях, когда рассматриваются решетки, работающие на пропускание света, используется так называемый «плазмонный эффект» [9, 10], представляющий собой предмет отдельного рассмотрения. Тем не менее, принцип работы ряда оптико-электронных приборов основан на применении конической дифракции при работе дифракционных решеток на прохождение света [11].

Основной особенностью обычных (амплитудных) дифракционных решеток, работающих на пропускание света, является то, что энергия дифрагированных лучей сосредоточена в основном в нулевом порядке дифракции. Если для дифракционных решеток, работающих на отражение, разработаны эшеллеты, т.е. фазовые дифракционные решетки, концентрирующие энергию в требуемом порядке дифракции [1, 2], то для решеток, работающих на пропускание света, аналогичных разработок нет. Однако имеются исследования, направленные на определение дифракционной эффективности в различных порядках дифракции рельефно-фазовых дифракционных решеток, работающих на пропускание света [12, 13].

В перечисленных публикациях рассматриваются идеализированные рельефно-фазовые дифракционные решетки. В то же время имеются упоминания об ограничениях электромагнитной и скалярной теорий, используемых при расчете таких решеток. В результате, применение на практике рекомендуемых аналитических выражений крайне затруднено. В связи с этим, актуальным представляется экспериментальное исследование конической дифракции при работе на пропускание в части определения углов дифракции и дифракционной эффективности в различных порядках.

Методика экспериментальных исследований

Экспериментальные исследования проводили на специализированном оптическом стенде [14]. Схема наладки стенда представлена на рис. 1.

В качестве источника излучения применяли полупроводниковый лазер 1 с длиной волны λ = 532 нм. После отражения от зеркал 2 лазерный луч направлялся вдоль оси паза оптического стола. Для повышения точности измерений лазерный луч пропускали через отверстие в диафрагме 3 диаметром 0,4 мм. Для устранения негативных последствий дифракции лазерного луча на отверстии диафрагмы 3, применяли также собирающую линзу 4, которая фокусировала лазерный луч на исследуемую ДР, выполненную на образце 6, который, в свою очередь, был установлен на измерительном поворотном столике 5 (рис. 2).

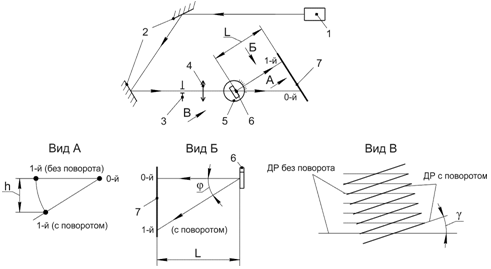
Рис. 1 - Оптический стенд: 1 – лазер; 2 – зеркала; 3 – диафрагма; 4 – собирающая линза; 5 – поворотный столик; 6 – образец; 7 – экран

 

Исследуемые образцы представляли собой набор дифракционных решеток с различными периодами (рис 3). Амплитудные дифракционные решетки изготавливали методом электронно-лучевой литографии на заготовках фотошаблонов для интегральных микросхем с хромовым покрытием. Фазовые дифракционные решетки получали плазмохимическим травлением, используя хромовое покрытие амплитудных дифракционных решеток в качестве маски [11].

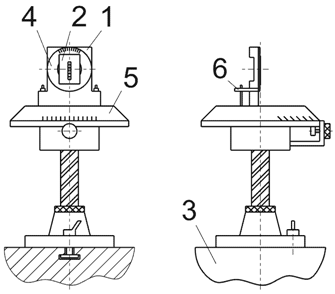
Рис. 2 - Установка образца на поворотном столике: 1 – держатель образца; 2 – образец; 3 – оптический стол; 4 – поворотное кольцо со шкалой; 5 –поворотный столик; 6 – прижимы

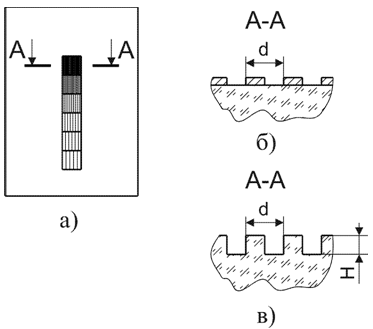
Рис. 3 - Конструктивное устройство исследуемых образцов: а – внешний вид; б – амплитудная дифракционная решетка; в – рельефно-фазовая дифракционная решетка

Исследовали образцы с периодами дифракционных решеток d = 800 и 1000 нм. В результате плазмохимического травления получали микрорельеф глубиной от 50 до 250 нм.

Угол поворота γ  задавали и измеряли при помощи специально изготовленного приспособления со шкалой. Это приспособление устанавливали и закрепляли на поворотном столике 5 (см. рис. 2).

Угол отклонения φ определяли, замеряя расстояние L между образцом и экраном, а также, замеряя на самом экране расстояние h, на которое смещается точка первого порядка дифракции при повороте образца на угол.

Интенсивности световых потоков замеряли специальным измерителем мощности лазерного излучения, включавшим измерительную головку с фотодиодом и специальное программное обеспечение [15].

Результаты экспериментальных исследований и их обсуждение

Экспериментально определили взаимосвязь между углом поворота γ и углом φ отклонения луча, дифрагированного на провернутой ДР.

На рис. 4 совмещены результаты измерений амплитудных и фазовых дифракционных решеток (ДР). ДР с периодом d = 1000 нм обозначены кружочками, а ДР с периодами d = 800 нм обозначены квадратиками. При этом фазовым ДР соответствуют закрашенные фигуры, а амплитудным – незакрашенные.

Из рассмотрения графиков на рисунке 4 можно сделать следующие выводы:

- зависимости углов отклонения φ от углов поворота γ для амплитудных и фазовых ДР идентичны;

- углы отклонения φ и поворота γ не совпадают (не равны между собой);

- углы отклонения φ (во всяком случае, в исследованном диапазоне периодов дифракционных решеток d = 800 – 1000 нм) меньше, чем углы поворота γ;

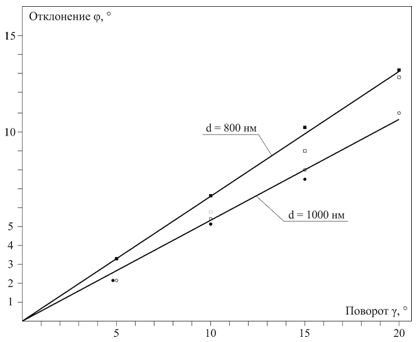
Рис. 4 - Экспериментальная зависимость угла отклонения φ от угла  поворота γ

 

- зависимость углов отклонения от углов поворота линейная и описывается формулой

φ = kγ ,   (1)

где k – коэффициент пропорциональности, найденный эмпирически.

Можно считать, что для периода ДР d = 1000 нм k = 0,51, а для периода ДР d = 800 нм k = 0,65.

В теоретических работах по определению зависимости дифракционной эффективности ДР от глубины профиля Н рассматривается только нормальное падение луча на ДР, тогда как практический интерес представляет данная зависимость и при наклонном падении для достижения максимальной интенсивности в рабочем порядке.

Для эмпирического установления влияния периода на дифракционную эффективность фазовых ДР была изготовлена линейка, состоящая из фазовых  ДР с периодами d = 800, 900, 1000, 1100, 1200, 1300 нм.  Глубина канавок всех этих ДР одинакова, т.к. они получены за одну операцию ПХТ. Цель исследования заключалась в установлении факта влияния периода фазовой ДР (точнее – соотношения между периодом ДР d и длиной волны λ падающего пучка лазерного излучения) на ее дифракционную эффективность.

Указанное экспериментальное исследование осуществляли на оптическом стенде, схема которого представлена на рис. 1.

Интенсивность лазерного излучения замеряли компьютеризированным прибором, измерительную головку которого помещали на пути распространения лазерного луча до ДР (зона Б) и после ДР (зона А). При этом в зоне Б замерялась интенсивность недифрагированного лазерного луча, а в зоне А замерялись интенсивности дифрагированного лазерного луча в 0-м и  1-м порядках дифракции.

Изменения проводили для двух случаев расположения образца:

- при ортогональном падении излучения на образец;

- при наклонном падении излучения на образец.

Во втором случае (т.е. при наклонном падении излучения на образец) угол поворота образца выбирали таким образом, чтобы луч первого порядка дифракции распространялся перпендикулярно к плоскости образца: для периодов ДР d = 800, 900, 1000, 1100, 1200, 1300 нм эти углы поворота (они же углы падения θ) составили соответственно: θ = 43⁰, 37⁰, 33⁰, 29⁰, 26⁰, 26⁰.

Результаты измерений представлены на рис. 5. Угол падения θ изменяли в зависимости от периода исследуемой ДР.

Можно видеть, что при наклоне образца интенсивность проходящего через стекло лазерного излучения уменьшается, что обусловлено явлением возрастания коэффициента отражения с увеличением угла падения. Можно видеть, что для периода дифракционной решетки d = 1000 нм наблюдается предсказываемое теорией ослабление интенсивности излучения в 0-м порядке при одновременном увеличении этой интенсивности в 1-м порядке дифракции. Этот факт обосновывает эмпирически возможность перераспределения интенсивности лазерного излучения из 0-го порядка дифракции в 1-йза счет создания именно рельефно-фазовой дифракционной решетки взамен амплитудной. Эта возможность усиливается при наклонном падении лазерного луча на ДР.

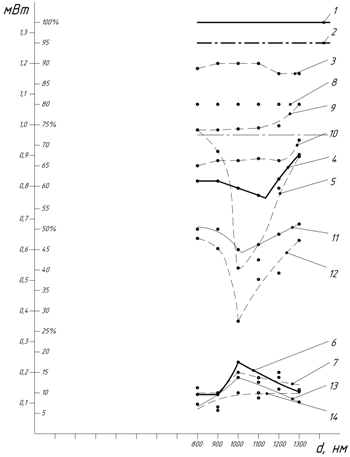
Рис. 5 - Экспериментальные зависимости дифракционной эффективности от периода ДР: 1- полная интенсивность лазерного излучения, замеренная в зоне Б; 2 - интенсивности лазерного излучения, замеренная в зоне А, при ортогональном падении лазерного луча на образец и при прохождении луча только через стекло; 3 – то же, что и 2, но при различных исследованных углах наклона образца; 4 - интенсивность лазерного излучения в 0-м порядке дифракции при ортогональном падении лазерного луча; 5 – то же, что и 4, но при наклонном падении лазерного луча; 6 и 7 - интенсивности лазерного излучения в 1-м порядке дифракции при ортогональном (линия 6) и наклонном (линия 7) падении лазерного луча; 8 - мощность падающего излучения в зоне Б, выраженная в Ваттах; 9 и 10 – мощность в Ваттах в зоне А при ортогональном (9) и  наклонном (10) падении; 11 и 12 - интенсивности дифрагированного лазерного излучения в 0-м порядке дифракции при ортогональном (11)  и наклонном (12) падении луча на образец; 13и 14 - интенсивности дифрагированного лазерного излучения в 1-м порядке дифракции при ортогональном (13)  и наклонном (14) падении.

 

Также было проведено экспериментальное установление взаимосвязи между глубиной рельефа Н фазовой ДР и получаемой дифракционной эффективностью. Дифракционную эффективность оценивали, как доли интенсивностей света в 0-м и 1-м порядках дифракции в общей интенсивности прошедшего через образец света. При этом за общую интенсивность прошедшего через образец света принимали интенсивность, замеренную в зоне Б.

На рисунке 6 показаны полученные эмпирические зависимости для образца с периодом d = 1000 нм.

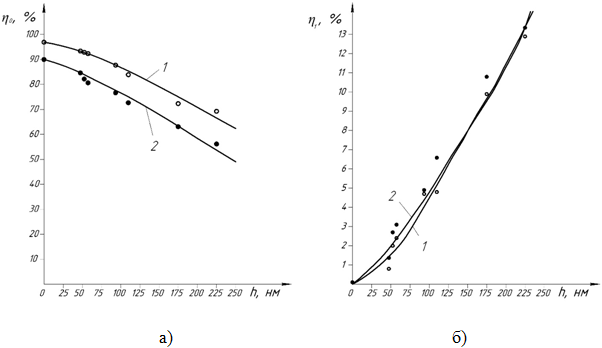
Рис. 6 - Доля прошедшего излучения: а) – для 0-го порядка; б) – для 1-го порядка. 1 – нормальное падение луча на решетку θ = 0°; 2 – θ  = 32°

Из рассмотрения графиков на рисунке 6 видно, что с увеличением глубины канавок, формирующих рельеф фазовой дифракционной решетки, происходит перераспределение интенсивности света между порядками дифракции, что согласуется с теорией [12]. При выборе высоты профиля Н нужно стремиться к тому, чтобы интенсивность света в 0-м порядке была минимальной, а в 1-м максимальной.

Выводы

Угол отклонения φ дифрагированных в первом порядке лучей линейно зависит от угла поворота линий дифракционных решеток γ. Эту зависимость можно описать эмпирически установленной формулой (1). При этом коэффициент пропорциональности k уменьшается с увеличением периода d решетки.

Фазовые ДР позволяют сфокусировать максимум интенсивности света в нужном порядке дифракции, перераспределение можно осуществить выбором глубины канавок, образующих профиль фазовой ДР.

Литература

1. Ландсберг Г.С. Дифракция при косом падении света на решётку // Элементарный учебник физики. — 13-е изд.— Т. 3. Колебания и волны. Оптика. Атомная и ядерная физика. — М.: Физматлит, 2003. — С. 347-348.
2. Born M., Wolf E. Principles of Optics. – Pergamon, 1980. – P. 598.
3. Moharam M.G., Gaylord T.K. Three-dimensional vector coupled-wave analysis of planar-grating diffraction. - J. Opt. Soc. Am. – 1983. Vol. 73. - P. 1105- 1112.
4. Harvey J.E., Venold C.L. Description of Diffraction Grating Behavior in Direction Cosine Space. - Appl. Opt. – 1998. Vol. 37. – P. 8158–8160.
5. An EUV beamsplitter based on conical grazing incidence diffraction / C. Braig, L. Fritzsch, T. Kasebier, E.-B. Kley, C. Laubis, Y. Liu, F. Scholze and A. Tunnermann. - Optics Express. – 2012. Vol. 20, № 2. – P. 1825 – 1838.
6. Virtual display design using waveguide hologram in conical mounting configuration / Z. Yan, W. Li, Y. Zhou, M. Kang and Z. Zheng. - Optical Engineering 50(9), 094001 (September 2011). – P. 1 – 8.
7. Harvey J. E., Krywonos A., Bogunovic D. Nonparaxial scalar treatment of sinusoidal phase gratings. - J. Opt.  Soc. Am. A . - 2006. Vol. 23, No. 4. – P. 858 – 865.
8. Angular distribution of light scattered from a sinusoidal grating / E. Marx, Th.A. Germer, Th.V. Vorburger and B.C. Park. - Applied Optics. - 2000. Vol. 39, No. 25. - P. 4473-4485.
9. Ruffato G., Zacco G., Romanato F. Innovative Exploitation of Grating-Coupled Surface Plasmon Resonance for Sensing / Plasmonics – Principles and Applications. - http://dx.doi.org/10.5772/51044. – P. 419 – 444.
10. Plasmonic grating as a nonlinear converter-coupler / N. Talebi, M. Shahabadi, W. Khunsin and R. Vogelgesang. – Optics Express. – 2012. Vol. 20, No. 2. – P. 1392 – 1405.
11. Одиноков С.Б., Сагателян Г.Р., Ковалев М.С. Расчет, конструирование и изготовление дифракционных и голограммных оптических элементов: учебное пособие. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2014. – 121 с.
12. Knop K. Rigorous diffraction theory for transmission phase gratings with deep rectangular grooves. - J. Opt. Soc. Am. - 1978. Vol. 68, No.9. – P. 1206 – 1210.
13. Настас А.М., Иову М.С. Исследование влияния глубины рельефа на дифракционную эффективность отражающей и пропускающей рельефно-фазовых дифракционных решеток. - Журнал технической физики. – 2015. Т. 85, №7. –– С. 133-134.
14. Исследование амплитудной и фазовой модуляционных характеристик жидкокристаллического пространственного модулятора света в оптической системе голографической памяти / С.Б. Одиноков, В В. Маркин, А.Ю. Павлов, Д.С. Лушников, А.О. Борисанова - Вестник МГТУ им. Н.Э. Баумана. Сер. “Приборостроение”. - 2011. № 3. – С. 34 – 50.
15. Разработка стенда для получения малогабаритного голографического индикатора отображения знаково-символьной информации / С.Б. Одиноков, В.В. Колючкин, В.В. Маркин, А.Б. Соломашенко. - Естественные и технические науки. - № 1 (63), 2013. - С. 196-198

References

1. Landsberg G.S. Difrakcija pri kosom padenii sveta na reshjotku // Jelementarnyj uchebnik fiziki. — 13-e izd.— T. 3. Kolebanija i volny. Optika. Atomnaja i jadernaja fizika. — M.: Fizmatlit, 2003. — S. 347-348.
2. Born M., Wolf E. Principles of Optics. – Pergamon, 1980. – P. 598.
3. Moharam M.G., Gaylord T.K. Three-dimensional vector coupled-wave analysis of planar-grating diffraction. - J. Opt. Soc. Am. – 1983. Vol. 73. - P. 1105- 1112.
4. Harvey J.E., Venold C.L. Description of Diffraction Grating Behavior in Direction Cosine Space. - Appl. Opt. – 1998. Vol. 37. – P. 8158–8160.
5. An EUV beamsplitter based on conical grazing incidence diffraction / C. Braig, L. Fritzsch, T. Kasebier, E.-B. Kley, C. Laubis, Y. Liu, F. Scholze and A. Tunnermann. - Optics Express. – 2012. Vol. 20, № 2. – P. 1825 – 1838.
6. Virtual display design using waveguide hologram in conical mounting configuration / Z. Yan, W. Li, Y. Zhou, M. Kang and Z. Zheng. - Optical Engineering 50(9), 094001 (September 2011). – P. 1 – 8.
7. Harvey J. E., Krywonos A., Bogunovic D. Nonparaxial scalar treatment of sinusoidal phase gratings. - J. Opt.  Soc. Am. A . - 2006. Vol. 23, No. 4. – P. 858 – 865.
8. Angular distribution of light scattered from a sinusoidal grating / E. Marx, Th.A. Germer, Th.V. Vorburger and B.C. Park. - Applied Optics. - 2000. Vol. 39, No. 25. - P. 4473-4485.
9. Ruffato G., Zacco G., Romanato F. Innovative Exploitation of Grating-Coupled Surface Plasmon Resonance for Sensing / Plasmonics – Principles and Applications. - http://dx.doi.org/10.5772/51044. – P. 419 – 444.
10. Plasmonic grating as a nonlinear converter-coupler / N. Talebi, M. Shahabadi, W. Khunsin and R. Vogelgesang. – Optics Express. – 2012. Vol. 20, No. 2. – P. 1392 – 1405.
11. Odinokov S.B., Sagateljan G.R., Kovalev M.S. Raschet, konstruirovanie i izgotovlenie difrakcionnyh i gologrammnyh opticheskih jelementov: uchebnoe posobie. – M.: Izd-vo MGTU im. N.Je. Baumana, 2014. – 121 s.
12. Knop K. Rigorous diffraction theory for transmission phase gratings with deep rectangular grooves. - J. Opt. Soc. Am. - 1978. Vol. 68, No.9. – P. 1206 – 1210.
13. Nastas A.M.,M Iovu .S. Issledovanie vlijanija glubiny rel'efa na di-frakcionnuju jeffektivnost' otrazhajushhej i propuskajushhej rel'efno-fazovyh difrakcionnyh reshetok. - Zhurnal tehnicheskoj fiziki. – 2015. T. 85, №7. –– S. 133-134.
14. Issledovanie amplitudnoj i fazovoj moduljacionnyh harakteristik zhidkokristallicheskogo prostranstvennogo moduljatora sveta v optiche-skoj sisteme golograficheskoj pamjati / S.B. Odinokov, V V. Markin, A.Ju. Pavlov, D.S. Lushnikov, A.O. Borisanova - Vestnik MGTU im. N.Je. Bau-mana. Ser. “Priborostroenie”. - 2011. № 3. – S. 34 – 50.
15. Razrabotka stenda dlja poluchenija malogabaritnogo golograficheskogo indikatora otobrazhenija znakovo-simvol'noj informacii / S.B. Odinokov, V.V. Koljuchkin, V.V. Markin, A.B. Solomashenko. - Estestvennye i tehni-cheskie nauki. - № 1 (63), 2013. - S. 196-198.