ЧИСЛЕННОЕ ИССЛЕДОВАНИЕ ДИНАМИКИ РАСШИРЕННОЙ МОДЕЛИ РЕАКЦИИ БЕЛОУСОВА-ЖАБОТИНСКОГО

Икрамов Р.Д.¹, Мустафина С.А.²

¹ORCID: 0000-0003-0325-7859, Аспирант, ²Доктор физико-математических наук, Стерлитамакский филиал Башкирского государственного университета

ЧИСЛЕННОЕ ИССЛЕДОВАНИЕ ДИНАМИКИ РАСШИРЕННОЙ МОДЕЛИ РЕАКЦИИ БЕЛОУСОВА-ЖАБОТИНСКОГО

Аннотация

В статье рассмотрена одна из моделей колебательной реакции Белоусова-Жаботинского – 6-ти стадийная модель Орегонатора. При проведении численного исследования использован L-устойчивый метод на основе АВС-схемы с действительными коэффициентами, подходящий для решения систем дифференциальных уравнений с высоким коэффициентом жесткости. Для модели Орегонатора проведен анализ колебаний, найдены периоды колебаний. Реакция Белоусова-Жаботинского является ярким примером колебательных химических реакций.

Ключевые слова: реакция Белоусова-Жаботинского, Орегонатор, колебания, осцилляции.

Ikramov R.D.¹, Mustafina S.A.²

¹ORCID: 0000-0003-0325-7859, Postgraduate student, ²PhD in Physics and Mathematics, Sterlitamak Branch of Bashkir State University

NUMERICAL INVESTIGATION OF DYNAMICS OF THE EXTENDED MODEL OF THE BELOUSOV-ZHABOTINSKI REACTION

Abstract

6-stage Oregonator model, one of the models of the oscillating Belousov-Zhabotinski reaction, was considered in the article. L-stable method based on ABC-scheme with real coefficients is used for solving differential equations system. Method is appropriate for systems with high stiffness coefficient. Article considered analysis of oscillations, values of the periods of oscillations. Belousov-Zhabotinski’s reacton is the one of the greatest chemical oscillating reaction.  

Keywords: Belousov-Zhabotinski’s reacton, Oregonator, oscillations.

Большинство химических превращений протекает через огромное количество элементарных стадий с большим числом различных интермедиантов, которые могут включать атомы и радикалы. При этом их концентрации не всегда описываются возрастающими или убывающими кривыми. При этом стоит учитывать трудность экспериментальной регистрации малых концентраций промежуточных веществ, а большое количество перекрестных взаимодействий между веществами лишь усложняет исследование реакции.

Колебательными называются реакции, в которых происходит периодическое изменений концентраций веществ, участвующих в самой реакции.

Колебательные процессы играют важную роль не только в химии, но также и биологии, биохимии и в других отраслях наук. Моделирование колебательных процессов позволяет понять, как протекают те или иные явления, происходящие в организме человека (колебания сердечной мышцы, биоритмы), в каталитических реакциях и т.д. Таким образом, исследование колебательных процессов и реакций является на сегодняшний день актуальной задачей.

Основная трудность при решении задач, описывающих колебательные процессы, заключается в необходимости обеспечения правильных значений амплитуд и фаз на протяжении многих периодов. Основная причина этому заключается в большом значении коэффициента жесткости и высокой размерности системы дифференциальных уравнений (СДУ) математических моделей. Поскольку характер поведения и тип СДУ может меняться в ходе интегрирования, то подбор численного метода интегрирования является важным этапом в процессе исследования колебательных процессов.

В начале XXI-го века в связи с бурным развитием компьютерных и информационных технологий вновь возник интерес к нестационарным и нелинейным явлениям в химической кинетике, называемых критическими [1]. Они характеризуются, в основном, множественностью стационарных состояний и автоколебаниями. Автоколебательными системами, в свою очередь, называются такие системы, проявляющиеся, во-первых, в незатухающих колебаниях вне зависимости от начальных условий, во-вторых, в их устойчивости по отношению к отклонениям от стационарного режима. Таким образом, в автоколебательной системе устанавливаются и поддерживаются незатухающие колебания за счет сил, зависящих от состояния системы [2].

Наиболее известной автоколебательной гомогенной реакцией считается реакция Белоусова-Жаботинского, в гетерогенных реакциях автоколебания были найдены Г.К. Боресковым и М.Г. Слинько.

В 1951 году Б.П. Белоусов открыл и экспериментально исследовал химическую реакцию окисления лимонной кислоты броматом,  катализируемой ионами металлов в кислой среде.  Возникающий в реакции колебательный режим с периодической сменой окраски стал классическим примером колебательных реакций [4]. Таким образом, Б.П. Белоусов внес основной вклад в открытие колебательных химических реакций. Позднее в 1955 г. И.Р. Пригожин доказал возможность существования в открытой системе химических колебаний около стационарного состояния, достаточно удаленного от термодинамического равновесия.

Механизм реакции Белоусова-Жаботинского насчитывает более 80 стадий, очевидно, что исследование закономерностей, а также решение прямой, обратной, оптимизационной задач не является возможным. Ученые из штата Орегон Р. Филд, Е. Кёрёш, Р. Нойес предложили механизм реакции Белоусова-Жаботинского, состоящий из 11 реакций между 15 различными соединениями, причем концентрации соединений достаточно сильно изменяются в ходе колебательного цикла [5]. Поэтому кинетика реакции может быть описана системой нелинейных обыкновенных дифференциальных уравнений первого порядка, полученных применением закона действующих масс к каждой стадии, чаще всего решаемых численно. Для исследования колебаний, бистабильности и бегущих волн аналитически необходимо сведение полной модели к более простой. Р. Филд и Р. Нойес первыми показали, что механизм Филда-Кереша-Нойеса может быть упрощен до поддающейся анализу математической модели. Поэтому авторами работы [6] была предложена абстрактная и простая модель реакции Белоусова-Жаботинского под названием «Орегонатор», которую впоследствии расширили [7] до шести стадий:

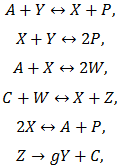
где  (бромат-ион), C = M(n) – ион металла катализатора, P = HOBr  (бромноватистая кислота), W = BrO₂ (диоксид брома), X = HBrO₂ (бромистая кислота), Y = Br^- (бромид-ион), Z = M(n+1) – окисленная форма иона металла катализатора, g – стехиометрический множитель.

Математическая модель Орегонатора, дающего сложный предельный цикл, имеет вид [8]:

где v₁,...,v₆ задаются следующими соотношениями:

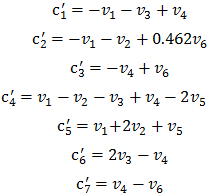
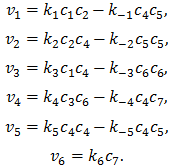
Концентрации реагентов обозначены следующим образом:

Константы скорости принимают следующие значения (M^-1c^-1):

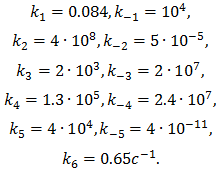
Основная трудность в моделировании колебательных химических реакциях заключается в разработке численных алгоритмов, достаточно точных и устойчивых для получения адекватных и качественно точных результатов [9]. Так как константы скорости различаются между собой на многие порядки, то коэффициент жесткости системы (1) принимает большое значение [10]. В силу этого, использование явных численных схем не представляется возможным. Для численного исследования модели (1) использовалась явно-неявная АВС-схема с действительными коэффициентами [11]:

где c(t) – численное решение системы (1) на шаге интегрирования в момент времени t с шагом h, f_y – матрица Якоби системы дифференциальных уравнений (1), E – единичная матрица. Данная схема является L-устойчивой и обладает вторым порядком точности.

Результаты интегрирования системы (1) при начальных условиях (М) :

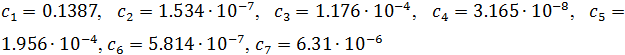
представлены на рис.1 (а-ж). Шаг интегрирования h = 10^-3.

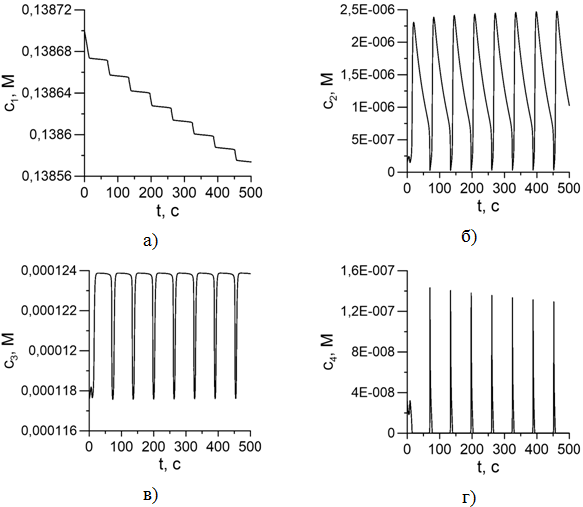
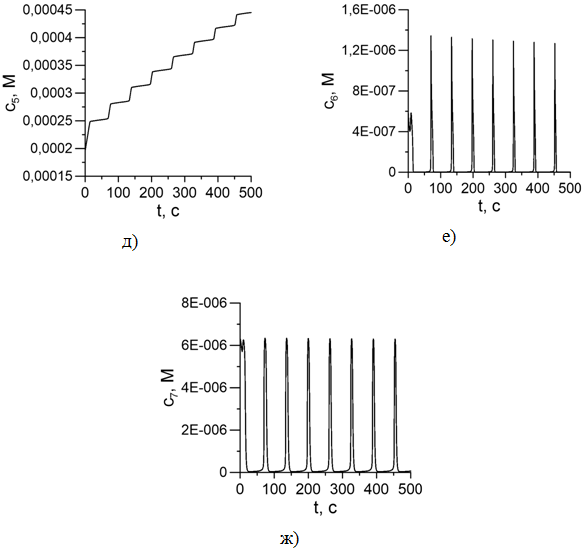
Рис. 1 - Колебания значений концентрации реагентов в зависимости от времени в модели (1):  

По рис. 1 видно, что модель Орегонатора (1) характеризуется длительными постепенно затухающими колебаниями. Реагент  характеризуется постепенным периодическим уменьшением своей концентрации, поскольку является исходным реагентом. Реагент характеризуется постепенным увеличением своей концентрации, накапливаясь как продукт реакции. Остальные компоненты системы характеризуются релаксационными режимами колебаний с быстрыми скачками. Период скачков составляет T ≈ 63.5 сек и постепенно увеличивается [12]. Суммарная концентрация катализатора и его иона остается постоянной, что подтверждает адекватность данной модели.

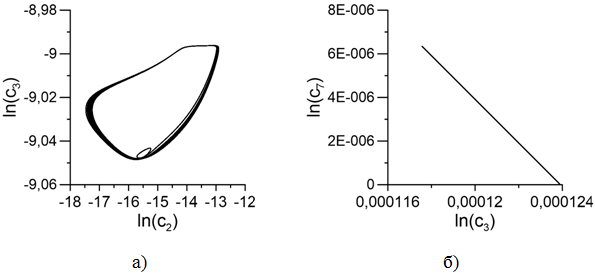
Рис. 2. Фазовые портреты модели (1): а) зависимость концентрации   , б)  

 

На рис. 2 представлены фазовые портреты в логарифмической плоскости, представляющие собой зависимости значений концентраций одного реагента от другого. На рис. 2а представлена зависимости концентрации металла катализатора от концентрации бромид-иона. Фазовый портрет представляет собой предельный цикл, замкнутые круговые области, что говорит, что в данной системе наблюдаются автоколебания. На рис. 2б представлен предельный цикл, вырожденный в прямую линию, что говорит о логарифмической зависимости между концентрациями катализатора и его иона.

Литература

1. Быков В. И. Моделирование критических явлений в химической кинетике. М.: Наука, 1988. 345 с.
2. Рубин А. Б., Пытьева Н. Ф., Ризниченко Г.Ю. Кинетика биологических процессов. Учебное пособие. М.: Изд-во Моск. ун-та, 1977. 330 с.
3. Lotka A. J. Elements of Physical Biology. Baltimore: Williams & Wilkins Company, 1925. 460 p.
4. Жаботинский А.М. Концентрационные колебания. М.: Наука, 1974. 179 с.
5. Жаботинский А.М., Отмер Х., Филд Р. Колебания и бегущие волны в химических системах. М.: Мир, 1988. 720 с.
6. Field R.J., Koros E., Noyes R.M. Oscillations in chemical systems. IV. Limit cycle Behavior in a model of real chemical reaction // J. Chem. Phys. – 1974. – Vol. 60. – P. 1877-1884.
7. Showalter K., Noyes R.M., Ber-eli K. A modified Oregonator exhibiting complicated limit cycle behavior in a flow system // J. Chem. Phys. – 1978. – Vol. 69. – P. 2514-2524.
8. Икрамов Р.Д., Мустафина С.А. Численное исследование моделей реакции Белоусова-Жаботинского на основе двухстадийного метода Розенброка с комплексными коэффициентами // Системы управления и информационные технологии. – 2014. - №2. – С. 11-14.
9. Икрамов Р.Д., Мустафина С.А. Численное исследование колебательных реакций с помощью метода Розенброка с действительными коэффициентами // Журнал Средневолжского математического общества. – 2014. – Т.16. - №1. – С.71-75.
10. Икрамов Р.Д., Мустафина С.А. Численное исследование моделей Орегонатора с использованием двухстадийного метода Розенброка с комплексными коэффициентами // Информационные технологии моделирования и управления. – 2014. - №6. – С. 211-217.
11. Булатов М.В., Тыглиян А.В., Филиппов С.С. Об одном классе одношаговых одностадийных методов для жестких систем обыкновенных дифференциальных уравнений // Журнал вычислительной математики и математической физики. – 2011. – Т.51. - №7. – С.1251-1265.
12. Икрамов Р. Д. Моделирование и численное исследование динамики колебательных химических реакций полунеявными методами: Автореф. дис. канд. физ.-мат. каук. – Уфа, 2016. – 24 с.

References

1. Bykov V. I. Modelirovanie kriticheskih javlenij v himicheskoj kinetike. M.: Nauka, 1988. 345 s.
2. Rubin A. B., Pyt'eva N. F., Riznichenko G.Ju. Kinetika biologicheskih processov. Uchebnoe posobie. M.: Izd-vo Mosk. un-ta, 1977. 330 s.
3. Lotka A. J. Elements of Physical Biology. Baltimore: Williams & Wilkins Company, 1925. 460 p.
4. Zhabotinskij A.M. Koncentracionnye kolebanija. M.: Nauka, 1974. 179 s.
5. Zhabotinskij A.M., Otmer H., Fild R. Kolebanija i begushhie volny v himicheskih sistemah. M.: Mir, 1988. 720 s.
6. Field R.J., Koros E., Noyes R.M. Oscillations in chemical systems. IV. Limit cycle Behavior in a model of real chemical reaction // J. Chem. Phys. – 1974. – Vol. 60. – P. 1877-1884.
7. Showalter K., Noyes R.M., Ber-eli K. A modified Oregonator exhibiting complicated limit cycle behavior in a flow system // J. Chem. Phys. – 1978. – Vol. 69. – P. 2514-2524.
8. Ikramov R.D., Mustafina S.A. Chislennoe issledovanie modelej reakcii Belousova-Zhabotinskogo na osnove dvuhstadijnogo metoda Rozenbroka s kompleksnymi kojefficientami // Sistemy upravlenija i informacionnye tehnologii. – 2014. - №2. – S. 11-14.
9. Ikramov R.D., Mustafina S.A. Chislennoe issledovanie kolebatel'nyh reakcij s pomoshh'ju metoda Rozenbroka s dejstvitel'nymi kojefficientami // Zhurnal Srednevolzhskogo matematicheskogo obshhestva. – 2014. – T.16. - №1. – S.71-75.
10. Ikramov R.D., Mustafina S.A. Chislennoe issledovanie modelej Oregonatora s ispol'zovaniem dvuhstadijnogo metoda Rozenbroka s kompleksnymi kojefficientami // Informacionnye tehnologii modelirovanija i upravlenija. – 2014. - №6. – S. 211-217.
11. Bulatov M.V., Tyglijan A.V., Filippov S.S. Ob odnom klasse odnoshagovyh odnostadijnyh metodov dlja zhestkih sistem obyknovennyh differencial'nyh uravnenij // Zhurnal vychislitel'noj matematiki i matematicheskoj fiziki. – 2011. – T.51. - №7. – S.1251-1265.
12. Ikramov R. D. Modelirovanie i chislennoe issledovanie dinamiki kolebatel'nyh himicheskih reakcij polunejavnymi metodami: Avtoref. dis. kand. fiz.-mat. kauk. – Ufa, 2016. – 24 s.