PRIORI ESTIMATES OF SOLUTIONS IN THE METRIC С0 (S) EQUATIONS OF MONGE-AMPERE ON THE SPHERE AS A TWO-DIMENSIONAL MANIFOLDS IN SPACES OF CONSTANT CURVATURE

Филимонова А.П.¹, Юрьева Т.А.²

¹Кандидат физико-математических наук, доцент, ²Кандидат педагогических наук, Амурский государственный университет

АПРИОРНЫЕ ОЦЕНКИ РЕШЕНИЯ В МЕТРИКЕ С⁰ () УРАВНЕНИЯ ТИПА МОНЖА-АМПЕРА НА СФЕРЕ КАК ДВУМЕРНОМ МНОГООБРАЗИИ В ПРОСТРАНСТВЕ ПОСТОЯННОЙ КРИВИЗНЫ

Аннотация

В статье приводится решение задачи о нахождении достаточных условий однозначной разрешимости дифференциального уравнения Монжа-Ампера на сфере как двумерном многообразии в пространствах постоянной кривизны, в частности в трехмерном пространстве Лобачевского. Рассматриваемая задача связанна с восстановлением поверхностей, гомеоморфных сфере, с заданной функцией гауссовой кривизны. В ходе доказательства теоремы получены априорные оценки решения уравнения типа Монжа-Ампера в метрике С⁰ (). Приведены следствия для частных видов уравнений Монжа-Ампера в трехмерном пространстве Лобачевского и в трехмерном евклидовом пространстве.

Ключевые слова: уравнение Монжа-Ампера, двумерное многообразие, априорные оценки, гауссова кривизна.

Filimonova A.P.¹, Yuryeva T.A.²

¹PhD in Physics and Mathematics, assосiate professor, ²PhD in Pedagogy, The Amur State University

PRIORI ESTIMATES OF SOLUTIONS IN THE METRIC С⁰ () EQUATIONS OF MONGE-AMPERE ON THE SPHERE AS A TWO-DIMENSIONAL MANIFOLDS IN SPACES OF CONSTANT CURVATURE

Abstract

The article provides a solution to the problem of finding sufficient conditions for the unique solvability of a differential equation of the Monge-Ampere equation on the sphere as a two-dimensional manifold in spaces of constant curvature, in particular three-dimensional Lobachevskii space. This problem is connected with the restoration of the surfaces, homeomorphic to a sphere with a predetermined function of the Gaussian curvature. In the course of the proof, a priori estimates of solutions of equations of the Monge-Ampere equation in the metric С⁰ (). Results investigation for particular types of Monge-Ampere equations in three-dimensional Lobachevskii space, in three-dimensional Euclidean space.

Keywords: Monge-Ampere equation, two-dimensional manifold, a priori estimates, the Gaussian curvature.

Рассмотрим следующую геометрическую задачу.

Пусть в трехмерном пространстве постоянной отрицательной кривизны (гиперболическом пространстве Лобачевского) Н³ фиксирована некоторая точка О. Пусть, далее,  – сфера единичного радиуса с центром в этой точке О. Будем рассматривать класс регулярных выпуклых гомеоморфных сфере  поверхностей, звездных относительно точки О. Произвольная поверхность F этого класса можно задать аналитически уравнением: F: ρ=ρ(u, v), где ρ, u, v – сферические координаты в пространстве Н³.

Рассмотрим сферу  как двумерное многообразие и выберем атлас так, чтобы в локальных координатах u, v каждой карты выполнялось неравенство: .

Пусть в Н³\{0} определена некоторая функция K_int(u, v, ρ)= K_int. Тогда задача о восстановлении поверхности F: ρ=ρ(u, v) в гиперболическом трехмерном пространстве Н³, гауссова (внутренняя) кривизна которой в каждой точке равна значению функции K_int в той же точке, сводится к нахождению достаточных условий однозначной разрешимости дифференциального уравнения типа Монжа-Ампера, которое на сфере  как двумерном многообразии имеет следующий вид [2]:

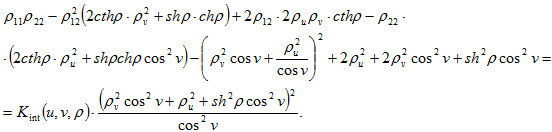 (1)

Здесь ρ_ij (i, j{1, 2}) – вторые ковариантные производные функции ρ=ρ(u, v)  относительно метрики единичной сферы .

В работе [2] показано, что уравнение (1) является отрицательно эллиптичным уравнением Монжа-Ампера при условии, что функция K_int(u, v, ρ)>-1 (K_ext(u, v, ρ)>0). Это означает, что если ρ=ρ(u, v) есть решение уравнения , то квадратичная форма отрицательно определена.

В [2] также доказана теорема о расположении поверхности F: ρ=ρ(u, v) (ρ=ρ(u, v) – решение уравнения (1)) при некоторых ограничениях на функцию K_int(u, v, ρ).

Теорема 1. Пусть в трехмерном гиперболическом пространстве Н³ фиксированы две концентрические сферы    с центром в точке О и радиусами ρ₁ и ρ₂ (ρ₁<ρ₂) соответственно.

Пусть функция K_int(u, v, ρ), определенная в  (R⁺– множество положительных действительных чисел), удовлетворяет следующим условиям:

1) K_int(u, v, ρ)>-1;

2)  внутри сферы  вне сферы .

Тогда любое решение ρ=ρ(u, v) дифференциального уравнения (1) задает поверхность F: ρ=ρ(u, v), лежащую между сферами  .

Аналитически результат теоремы означает, что при наложении условий теоремы 1 на функцию K_int=K_int(u, v, ρ) имеем априорные оценки решения дифференциального уравнения (1) в метрике С⁰(): .

Рассмотрим теперь обобщенное дифференциальное уравнение типа Монжа-Ампера на сфере  как двумерном многообразии [3]:

 (2)

В уравнении (2) ρ_ij (i, j{1, 2}) – вторые ковариантные производные функции ρ(u, v) относительно метрики единичной сферы , , а   (локальные географические координаты).

В работе [3] показано, что при наложении ограничений на входящие в (2) функции: φ(ρ)>0, φ₁(u, v)>0, φ₂(u, v)>0, f(ρ)>0, , (А, В, С коэффициенты при –ρ₁₁, 2ρ₁₂, –ρ₂₂),  уравнение (2) отрицательно эллиптично.

Квадратичная форма  для уравнения (2) имеет следующий вид:

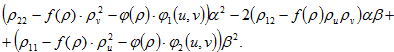
Докажем аналог теоремы 1 для обобщенного дифференциального уравнения (2), тем самым получим априорные оценки решения уравнения (2) в метрике С⁰().

Теорема 2. Пусть функция  удовлетворяет следующим условиям:

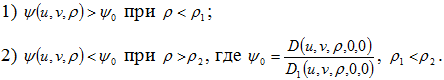
Тогда имеют место априорные оценки решения ρ=ρ(u,v) обобщенного дифференциального уравнения (2) в метрике ⁰(): .

Доказательство. Пусть  является решением дифференциального уравнения (2). Функция p=p(u,v) достигает на единичной сфере  минимального значения в некоторой точке (u₀,v₀) в силу того, что сфера  является компактным многообразием. В точке минимума (u₀,v₀) выполняются условия: . В экстремальных точках вторые ковариантные производные относительно метрики сферы  равны соответственно . Тогда d²p в точке (u₀,v₀) имеет вид: . Квадратичная форма  в точке минимума принимает вид:   в силу отрицательной эллиптичности дифференциального уравнения (2).

Рассмотрим выражение

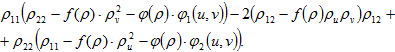
В точке (u₀,v₀) минимума функции ρ=ρ(u,v) данное выражение преобразуется: . Это выражение не является положительным в силу того, что ,  вследствие , а

Таким образом, 

Из полученного неравенства имеем:

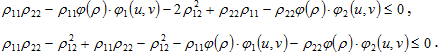
В силу определенности формы d²p в точке , отсюда следует, что

Дифференциальное уравнение (2) в точке минимума функции ρ=ρ(u,v) переходит в равенство:

Из этого равенства и полученного выше неравенства в точке (u,v) минимума функции ρ=ρ(u,v) следует справедливость следующего неравенства:

 следовательно,  (3)

Предположим, что . Тогда по условию теоремы 2 , а это противоречит полученному выше неравенству (3). Следовательно, . Оценка в метрике С⁰() снизу для решения дифференциального уравнения (2) получена .

Получим априорную оценку в метрике С⁰ () решения ρ(u,v) дифференциального уравнения (2) сверху. Рассмотрим следующую квадратичную форму: . Ее дискриминант равен

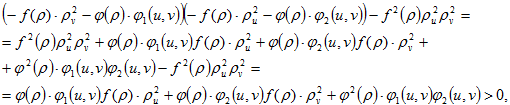
так как на функции  были наложены условия: _. Далее, коэффициент при  в силу тех же условий. Тогда 

Пусть, далее, (u₁,v₁) является точкой сферы, в которой функция ρ(u,v) достигает максимального значения. Это возможно в силу компактности сферы  как двумерного многообразия. Тогда в этой точке 

Рассмотрим выражение:

. В точке (u₁,v₁) максимума функции ρ(u,v) приведенное выше выражение примет вид: . Так как φ(ρ)>0, φ₁(u, v)>0, φ₂(u, v)>0, а в точке максимума , то имеем следующее неравенство: .

Дифференциальное уравнение (2) в точке (u₁,v₁) максимума функции p=ρ(u,v)  преобразуется в неравенство:

В точке  , следовательно,  силу определенности формы d²p. Тогда .

Из последнего неравенства и полученного из уравнения (2) равенства имеем: . Это означает, что . Таким образом, функция  в точке (u₁,v₁) максимума функции ρ=ρ(u,v) удовлетворяет неравенству:  (4).

Допустим, что . Тогда по условию теоремы 2 имеет место неравенство: , что противоречит полученному неравенству (4). Следовательно, . Это означает, что . Оценка сверху в метрике С⁰() решения  дифференциального уравнения (2) получена.

Таким образом, в целом имеем . Теорема доказана.

Следствие 1. Результат теоремы 2 совпадает с результатом теоремы 1 в случае рассмотрения уравнения (1) на   в трехмерном пространстве Лобачевского Н³.

Уравнение (1) есть частный случай уравнения (2). В самом деле, здесь

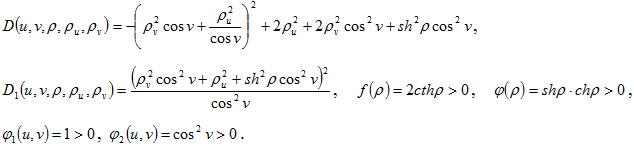
Тогда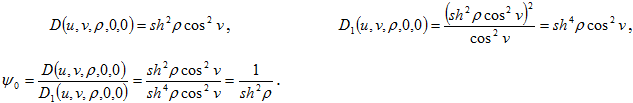 

Второе условие теоремы 1: , где  внутри сферы , равносильно условию . Аналогично, условие:  равносильно условию  , что совпадает с условиями теоремы 2.

Следствие.2 Геометрическая задача восстановления замкнутой выпуклой гомеоморфной сфере поверхности F в трехмерном евклидовом пространстве Е³. Рассматривается класс регулярных выпуклых гомеоморфных  поверхностей, звездных относительно точки О. Произвольная поверхность F этого класса задается уравнением: F: ρ=ρ(u, v), ρ, u, v – сферические координаты в Е³. Рассмотрим  как двумерное многообразие и выберем атлас так, чтобы в локальных координатах u, v каждой карты выполнялось неравенство: . Пусть в Е³\{0} определена функция K(u, v, ρ) . Тогда функция ρ=ρ(u, v), задающая поверхность F данного класса, в каждой точке которой гауссова кривизна равна значению функции K(u, v, ρ) в этой же точке, удовлетворяет следующему отрицательно эллиптичному уравнению типа Монжа-Ампера на  [1]:

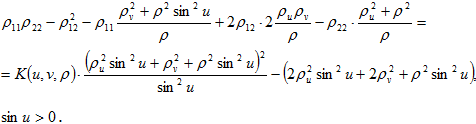  (5)

Уравнение (5) есть частный случай уравнения (2). Здесь ,

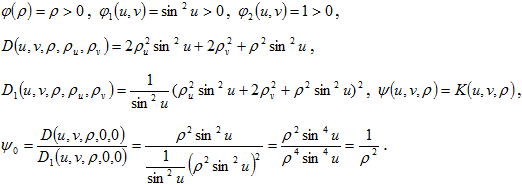
Тогда , то есть поверхность F при данных условиях расположена между сферами  и  в Е³ с радиусами ρ₁ и ρ₂ соответственно. Результат следствия 2 совпадает с результатом работы [1].

Литература

1. Верещагин Б.М. Восстановление замкнутой выпуклой поверхности по данной функции гауссовой кривизны // Вопросы глобальной геометрии: Сб. научн. трудов. – ЛГПИ им. Л. И. Герцена. – Л., 1979. – С. 7-12.
2. Филимонова А.П. Оценки в метрике С² и единственность выпуклой гомеоморфной сфере поверхности с заданной гауссовой кривизной в Н³ // Вопросы глобальной геометрии: Сб. научн. трудов. – ЛГПИ им. Л. И. Герцена. – Л., 1979. – С. 64-68.
3. Филимонова А.П., Юрьева Т.А. Единственность решения уравнения Монжа-Ампера некоторого класса на сфере как двумерном многообразии // Международный научно-исследовательский журнал. – 2016. – т № 6-5 (48). – С. 107-110.

References

1. Vereshhagin B.M. Vosstanovlenie zamknutoj vypukloj poverhnosti po dannoj funkcii gaussovoj krivizny // Voprosy global'noj geometrii: Sb. nauchn. trudov. – LGPI im. L. I. Gercena. – L., 1979. – P. 7-12.
2. Filimonova A.P. Ocenki v metrike С² i edinstvennost' vypukloj gomeomorfnoj sfere poverhnosti s zadannoj gaussovoj kriviznoj v Н³ // Voprosy global'noj geometrii: Sb. nauchn. trudov. – LGPI im. L. I. Gercena. – L., 1979. – P. 64-68.
3. Filimonova A.P., Jur'eva T.A. Edinstvennost' reshenija uravnenija Monzha-Ampera nekotorogo klassa na sfere kak dvumernom mnogoobrazii // Mezhdunarodnyj nauchno-issledovatel'skij zhurnal. – 2016. – t № 6-5 (48). – P. 107-110.