АНАЛИЗ РАЗЛИЧНЫХ МЕТОДОВ ОЦЕНКИ ИСТОРИЧЕСКОЙ ВОЛАТИЛЬНОСТИ ДЛЯ ОПЦИОННОЙ ТОРГОВЛИ

Смирнов А.

ORCID: 0000-0002-3601-6595, Магистр финансов, Санкт-Петербургский Государственный Экономический университет

АНАЛИЗ РАЗЛИЧНЫХ МЕТОДОВ ОЦЕНКИ ИСТОРИЧЕСКОЙ ВОЛАТИЛЬНОСТИ ДЛЯ ОПЦИОННОЙ ТОРГОВЛИ

Аннотация

В статье рассмотрены различные методы оценки исторической волатильности включающие различные рыночные особенности и степень сложности построения значения волатильности от наиболее простого базового метода (Close to Close), до методик Янг Жанга, а также произведён анализ оказываемого влияния различных оценок исторической волатильности на значение теоретической стоимости американского опциона, значение теоретической стоимости которого рассчитано на основе метода, предложенного Коксом, Россом и Рубинштейном.   

Ключевые слова: американские опционы, расчёт теоретической стоимости опциона на основе метода Кокса, Росса и Рубинштейна, оценка исторической волатильности.

Smirnov A.

ORCID: 0000-0002-3601-6595, Master in finance, Saint-Petersburg State University of Economics

ANALYSIS OF COMPUTATIONAL METHODS OF HISTORICAL VOLATILITY IN OPTION TRADING

Abstract

The article considers different methods of historical volatility estimation based on the different market features and difficulties of estimation from basic (close to close) method to Yang Zhang methods and analysis of the impact of different historical volatility methods on theoretical value of American type option based on Cox, Ross and Rubinstein method.

Keywords: American type option, computation of option theoretical value under the Cox, Ross and Rubinstein method, historical volatility estimation.

Сложность в определении исторической волатильности для оценки опционов является насущной проблемой для любого исследователя, поскольку в источниках литературы в основном представлена стандартная формула, для определения стандартного отклонения, при помощи которого оценивается волатильность цены базового актива. Однако, такой способ хоть и является наиболее простым, но не в состоянии учесть важные ньюансы, которые приводят к тому, что оцениваемая волатильность на самом деле будет недооценённой или наоборот переоценённой.

Так, наиболее распространённая формула нахождения исторической волатильности имеет вид:

  (1.1)

где С_i – это цена закрытия в промежуток i, С_i-1 – цена закрытия за предшествующий промежуток соответствующий значению i, а ln –натуральный логарифм [1].

Мы видим, что данная формула не учитывает важных особенностей изменения цены на рынке. В частности, при использовании такого метода оценки мы делаем предположение, что изменение цены – это сугубо диффузионный процесс, т.е. оно происходит плавно и не имеет резких скачков (гэпов), которые здесь сглаживаются. Однако, рыночные реалии показывают иную картину, которая является комбинацией диффузионного и скачкообразного процесса, что по сути делает стандартные метод оценки не столь эффективным. Метод также является недостаточно эффективным по той причине, что цена внутри интервала i также изменялась, чего данный метод оценки не учитывает.

Следующим звеном в эволюции оценки исторической волатильности является метод, предложенный исследователями Гарманом и Классом. Данный метод стал модификацией оценки Паркинсона, который рассматривал волатильность относительно экстремумов изменения цены актива за исследуемый временной интервал. Исследователи также делают предположение о том, что процесс изменения цены есть процесс непрерывной диффузии (геометрического броуновского движения), однако дополняют его значениями начальной и конечной цены актива, в этом случае методика расчёта волатильности выглядит следующим образом:

  [1]    (1.2.)

Однако мы уже упомянули, что цена является процессом не сугубо диффузионным, а диффузионно-скачкообразным, поэтому у данного метода есть недостатки, которые возникают в результате специфики метода оценки, поскольку метод не только не учитывает скачкообразной составляющей цены актива, но и отрицает возможность направленного движения актива в силу того, что в её основе лежит принцип случайного блуждания, которое не предполагает наличия трендовых движений. Однако данный метод, несмотря на свои недостатки, все же является более эффективным, чем базовая формула, поскольку учитывает не только цену на начало и конец временного интервала, но также и колебания цен до экстремумов интервала, что расширяет значение волатильности по сравнению с базовым методом оценки.

Следующий метод оценки исторической волатильности предложен исследователями Роджерсом и Сатчелом. По эффективности он незначительно превосходит предыдущий, однако имеет отличие в том, что позволяет учитывать направленное движение цены. Формула расчёта выглядит следующим образом:

 [1]      (1.3)

Недостаток данного метода выражен в том, что он не учитывает разрывы цен между сессиями, что говорит о недооценке волатильности, поскольку на рынке периодически случаются разрывы цен именно в моменты между сессиями.

Наиболее мощным методом оценки исторической волатильности является метод, разработанный в 2000-х годах на основе метода Роджерса-Сатчела. Метод был предложен исследователем Янг-Жангом и представляет собой не только оценку внутри интервальной волатильности, но также учитывает разрывы между сессиями. Расчёт волатильности по методу Янг-Жанга представлен следующими формулами:

  [1]     (1.4)

где k находится формулой:

 [1]    (1.5)

А  и   находятся по формулам (1.6), (1.7) соответственно:

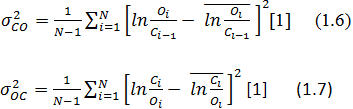
В итоге оценка по данному методу представляет собой средневзвешенную оценку по методу Роджерса-Сатчела, а также оценку волатильности между интервалами и внутри интервала, что представляет получить наиболее адекватную оценку исторической волатильности.

Несмотря на то, что представленные в данной статье методы оценки исторической волатильности не являются исчерпывающими, и выделены нами как наиболее представительные, все методы, кроме последнего, упускают те или иные аспекты оценки, что говорит о том, что такая оценка будет заниженной.

Практический аспект заниженной оценки выражается тем, что полученный параметр не позволит правильно оценить производный инструмент, и даже несмотря на тот факт, что будущая волатильность есть лишь величина предполагаемая, а также несмотря на более совершенные методы оценки, степень ошибки будет лишь варьироваться от метода к методу.

Для большей наглядности мы рассмотрим, каким образом все представленные выше методы повлияют на оценку американского опциона, произведённую по методу Кокса-Росса-Рубинштейна.

Для проведения оценки выберем инструмент в виде маржируемого опциона на фьючерсный контракт на обыкновенные акции ПАО «Сбербанк».

Так, для исследования исторической волатильности был выбран временной интервал с 22 января 2014 года по 21 июня 2016 года. Для оценки волатильности был использован временной интервал в 21 торговый день, что примерно равно одному месяцу. Оценка волатильности происходила по всем описанным выше методам, результаты представлены в таблице 1.

Таблица 1 - Результаты оценки исторической волатильности по различным методам для фьючерсов на обыкновенные акции ПАО «Сбербанк»

Использованный метод	Среднее значение месячной волатильности, в % годовых
Стандартная формула	33,51%
Метод Гармана-Класса	32,57%
Метод Роджерса-Сатчела	32,31%
Метод Янг-Жанга	36,75%

 

В результате, как и предполагалось, значение средней месячной волатильности по стандартному методу, методу Гармана-Класса и методу Роджерса-Сатчела значительно ниже, чем по методу Янг-Жанга.

Получив значение исторической волатильности, мы можем приступить к поиску теоретической стоимости американского опциона. Для расчета, кроме волатильности, нам потребуется значение нескольких параметров, в том числе: время до экспирации, цена исполнения, текущая цена фьючерского контракта, безрисковая процентная ставка, а также шаг по времени, для определения узлов модели.

В качестве параметров мы выбрали значение цены фьючерса на обыкновенные акции ПАО «Сбербанк» на момент закрытия 21 июня 2016 года или 13765 рублей за контракт. Момент экспирации опциона определён на 27 июля 2016 года, процентная ставка определена как краткосрочная ставка по ГКО-ОФЗ на 21 июня и равна 10,12%, шаг по времени определён в один торговый день и равен 0,0042, а цена исполнения равна 13750 рублей.

Параметры оценки шагов для модели при выбранных значениях представлены в таблице 2.

Таблица 2 - Параметры для уравнения Кокса, Росса и Рубинштейна [2]

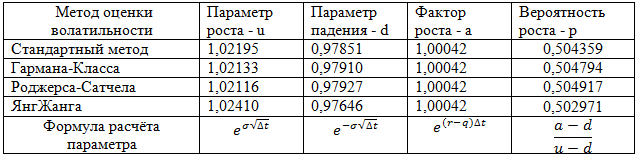
Таким образом из таблицы видно, что параметры, рассчитанные на основе волатильности по методам от стандартного до Роджерса-Сатчела, способствуют завышению вероятности роста, что сказывается не только на оценке опциона, но и на принятии решения о покупке или продаже того или иного опциона, также подобное расхождение скажется на принятии решения о досрочном исполнении американского опциона. Видно, что оценка значительным образом сказывается на всей модели, начиная с исходных параметров. Так, завышенная вероятность роста цены вызвана тем, что заниженные оценки волатильности в момент расчёта параметров роста или падения выставляют фактор роста завышенным, что в свою очередь ведёт к увеличению вероятности роста, и занижает вероятность падения цены. В результате опцион становится неверно оценённым, что значительным образом может повлиять на эффективность его использования.

Исходя из представленных параметров можно вывести теоретическую стоимость опциона. Теоретические стоимости опциона при заданных параметрах и различных методах оценки волатильности представлены в таблице 3.

Таблица 3 - Теоретические стоимости опционов при различных методах оценки волатильности

Метод оценки волатильности	Теоретическая стоимость опциона, в руб.
Стандартный метод	615,19
Метод Гармана-Класса	598,17
Метод роджерса-Сатчела	593,45
Метод ЯнгЖанга	673,89

 

Из таблицы 3 видно, что разброс в теоретической цене опциона составляет достаточно большую сумму, что в случае выбора стратегии продажи опциона, которая также становится привлекательнее в случае, когда параметры имеют завышенные или заниженные оценки, искажающие результат, могут принести значительно меньшую доходность, или, если издержки по поддержанию рыночной нейтральности по параметру дельта составляют значительную величину, принести убытки по позиции.

Выводы:

- Наиболее сложные модели оценки волатильности, такие как метод Янг-Жанга, имеют ряд значительных преимуществ, по сравнению с другими методами, поскольку учитывают диффузионно-скачкообразную природу цен, а также дрифт цены, что повышает качество оценки.

- Более качественная оценка волатильности позволяет увеличить эффективность нахождения теоретической стоимости опциона, а также использования опциона в качестве инструмента, как с целью спекуляции, так и с целью хеджирования.

- Правильная оценка волатильности, позволит более качественно оценить риски и принять более обоснованное решение относительно цены опциона, опираясь на конкретные количественные значения, а также не потерпеть убытки при правильном расчёте волатильности.

Литература

1. MEASURING HISTORICAL VOLATILITY [Electronic resource] URL: http://www.todaysgroep.nl/media/236846/measuring_historic_volatility.pdf (data obrashhenija 05.2016)
2. C. Cox, S. A. Ross, and M. Rubinstein, ‘‘Option Pricing: A Simplified Approach,’’ [Electronic resource] URL: http://fisher.osu.edu/~fellingham.1/seminar/CRR79.pdf (data obrashhenija 28.04.2016).